Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 12.2 Answer Key Properties of Reflections.
Texas Go Math Grade 8 Lesson 12.2 Answer Key Properties of Reflections
Texas Go Math Grade 8 Lesson 12.2 Explore Activity Answer Key
Explore Activity 1
Exploring Reflections
A reflection is a transformation that flips a figure across a line. The line ¡s called the line of reflection. Each point and its image are the same distance from the line of reflection.

The triangle shown on the grid is the preimage. You will explore reflections across the x- and y-axes.
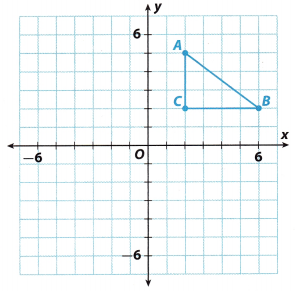
A. Trace triangle ABC and the x- and y-axes onto a piece of paper.
B. Fold your paper along the x-axis and trace the image of the triangle on the opposite side of the x-axis. Unfold your ‘ paper and label the vertices of the image A’, B’, and C’.
C. What is the line of reflection for this transformation?
D. Find the perpendicular distance from each point to the line of reflection.
Point A __________ Point B ___________ Point C ___________
E. Find the perpendicular distance from each point to the line of reflection.
Point A’ __________ Point B’ ___________ Point C’ ___________
F. What do you notice about the distances you found in D and E?
Reflect
Question 1.
Fold your paper from A along the y-axis and trace the image of triangle ABC on the opposite side. Label the vertices of the image A”, B”, and C”. What is the line of reflection for this transformation?
Answer:
The line of reflection for this transformation is y-axis.
Question 2.
How does each image in your drawings compare with its preimage?
Answer:
The triangle A’B’C’ is on the same distance from x-axis like triangle ABC.
The triangle A”B”C” is on the same distance from y-axis like triangle ABC.
Image and its preimage are the same distance from the line of reflection.
Explore Activity 2
Properties of Reflections
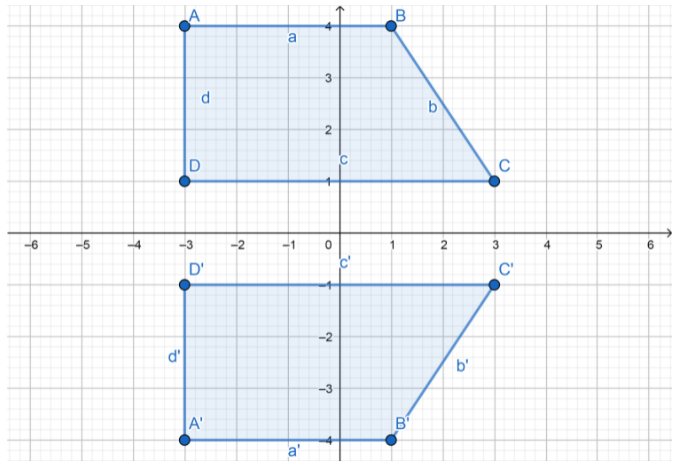
Use trapezoid TRAP to investigate the properties of reflections.
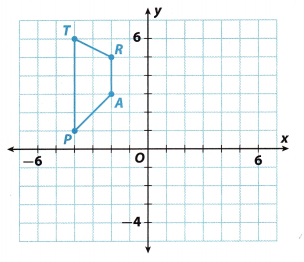
A. Trace the trapezoid onto a piece of paper. Cut out your traced trapezoid.
B. Place your trapezoid on top of the trapezoid in the figure. Then reflect your trapezoid across the y-axis. Sketch the image of the reflection by tracing your trapezoid in this new location. Label the vertices of the image T’,R’,A’, and P’.
C. Use a ruler to measure the sides of trapezoid TRAP in centimeters.
TR = ___________ RA = ___________ AP = ___________ TP = ___________
D. Use a ruler to measure the sides of trapezoid T’R’A’P’ in centimeters.
TR’= ___________ R’A’ = ___________ A’P’ = ___________ T’P’ = ___________
E. What do you notice about the lengths of corresponding sides of the two figures?
F. Use a protractor to measure the angles of trapezoid TRAP.
m∠T = ___________ m∠R = ___________ m∠A = ___________ m∠P = ___________
G. Use a protractor to measure the angles of trapezoid T’R’A’P’.
m∠T’ = ___________ m∠R’ = ___________ m∠A’ = ___________ m∠P’ = ___________
H. What do you notice about the measures of corresponding angles of the two figures?
I. Which sides of trapezoid TRAP are parallel? ___________
Which sides of trapezoid T’R’A’P’are parallel? ___________
What do you notice?
Reflect
Question 3.
Make a Conjecture Use your results from E, H, and I to make a conjecture about reflections.
Answer:
A reflection is a transformation that flips a figure across a line. This means that image of the figure and its preimage have the same size and shape, so they are congruent.
Your Turn
Question 4.
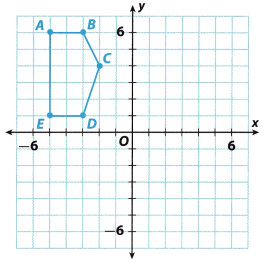
The figure shows pentagon ABCDE. Graph the image of the pentagon after a reflection across the y-axis.
Answer:
Step 1: Reflect point A.
Count 5 units from the other side of y-axis. Plot point A'(5, 6).
Step 2: Reflect point B.
Count 3 units from the other side of y-axis. Plot point B'(3, 6).
Step 3: Reflect point C.
Count 2 units from the other side of y-axis. PLot point C'(2, 4).
Step 4: Reflect point D.
Count 3 units from the other side of y-axis. Plot point D'(3, 1).
Step 5: Reflect point E.
Count 5 units from the other side of y-axis. Plot point E'(5, 1).
Step 6: Connect A’, B’, C’, D’ and E’ to form pentagon A’B’C’D’E’.
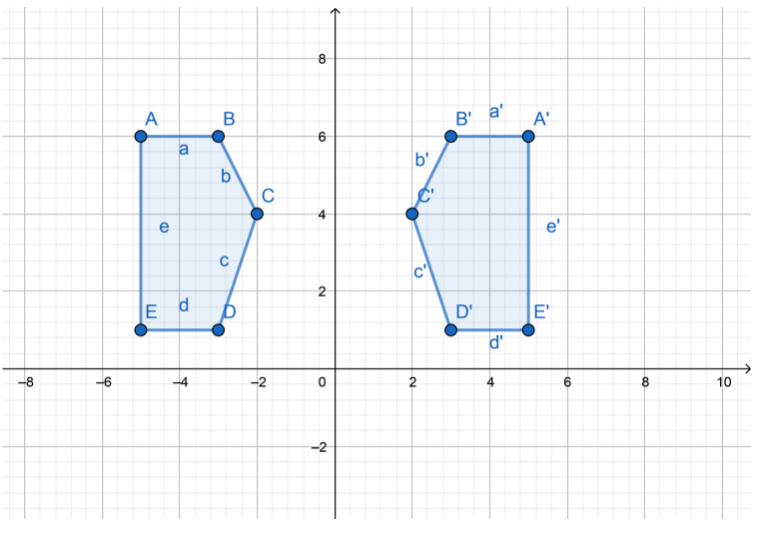
A'(5, 6)
B'(3, 6)
C'(2, 4)
D'(3, 1)
E'(5, 1)
Texas Go Math Grade 8 Lesson 12.2 Guided Practice Answer Key
Question 1.
Vocabulary A reflection is a transformation that flips a figure across a line called the ______________.
Answer:
A reflection is a transformation that flips a figure across a line called the line of reflection.
Question 2.
The figure shows trapezoid ABCD. (Explore Activities 1 and 2 and Example 1)
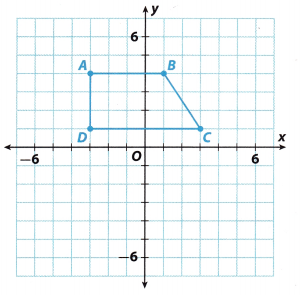
a. Graph the image of the trapezoid after a reflection across the x-axis. Label the vertices of the image.
Answer:
Step 1: Reflect point A.
Count 4 units below the x-axis. Plot point A'(-3, -4).
Step 2: Reflect point B.
Count 4 units below the x-axis. Plot point B'(1, -4).
Step 3: Reflect point C.
Count 1 unit below the x-axis. Plot point C'(3, -1).
Step 4: Reflect point D.
Count 1 unit below the x-axis. Plot point D'(-3, -1).
Step 5: Connect A’, B’, C’ and D’ to form trapezoid A’B’C’D’.
b. How do trapezoid ABCD and trapezoid A’B’C’D’ compare?
Answer:
Trapezoid ABCD and trapezoid A’B’C’D’ are congruent.
c. What If? Suppose you reflected trapezoid ABCD across the y-axis. How would the orientation of the image of the trapezoid compare with the orientation of the preimage?
Answer:
If we reflect trapezoid ABCD across the y-axis, the trapezoids would be oppositely oriented, in that case.
Essential Question Check-In
Question 3.
What are the properties of reflections?
Answer:
The properties of reflection is that image of geometric figure has the same size like preimage and the same shape, but different orientation.
Texas Go Math Grade 8 Lesson 12.2 Independent Practice answer Key
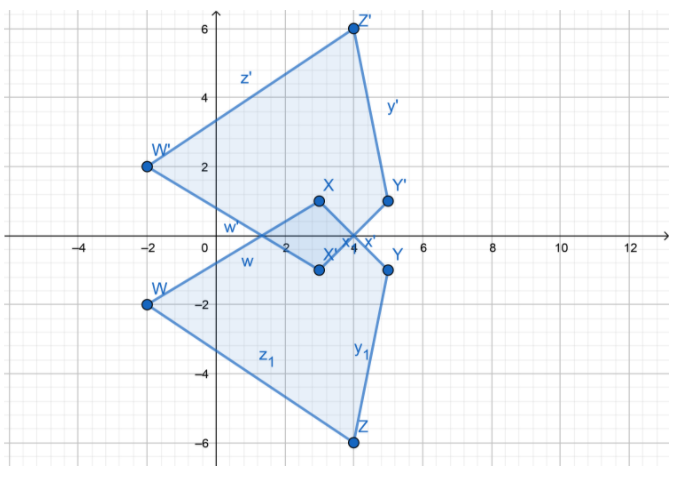
The graph shows four right triangles. Use the graph for Exercises 4-7.
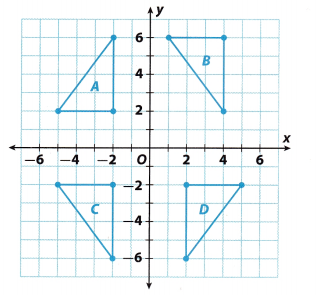
Question 4.
Which two triangles are reflections of each other across the x-axis?
Answer:
Triangles A and C are reflections of each other across the x-axis.
Question 5.
For which two triangles is the line of reflection the y-axis?
Answer:
Triangles C and D the line of reflection is the y-axis.
Question 6.
Which triangle is a translation of triangle C? How would you describe the translation?
Answer:
The triangle B is a translation of triangle C. The translation is 8 units up and 6 units right.
Question 7.
Which triangles are congruent? How do you know?
Answer:
The preimage and the image obtained by reflection and translation are congruent. The graph shows us 4 triangles obtained either by translation or reflection. This means that all 4 triangles are congruent.
Question 8.
a. Graph quadrilateral WXYZ with vertices W(-2, -2), X(3,1), Y(5, -1), and Z(4, -6) on the coordinate grid.
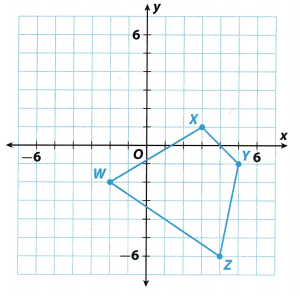
Answer:
Step 1: Reflect point W.
Count 2 units above the x-axis. PLot point W'(-2, 2).
Step 2: Reflect point X.
Count 1 unit below the x-axis. Plot point X'(3, -1).
Step 3: Reflect point Y.
Count 1 unit above the x-axis Plot point Y'(5, 1)
Step 4: Reflect point Z.
Count 6 units above the x-axis PLot point Z'(4, 6).
Step 5: Connect W’, X’, Y’ and Z’ to form quadrilateral W’X’Y’Z’.
b. On the same coordinate grid, graph quadrilateral W’X’Y’Z’, the image of quadrilateral WXYZ after a reflection across the x-axis.
Answer:
\(\overline{\mathrm{YZ}}\) is congruent to \(\overline{Y^{\prime} Z^{\prime}}\);
\(\overline{\mathrm{XY}}\) is congruent to \(\overline{X^{\prime} Y^{\prime}}\);
\(\overline{\mathrm{WZ}}\) is congruent to \(\overline{W^{\prime} Z^{\prime}}\),
\(\overline{\mathrm{XW}}\) is congruent to \(\overline{X^{\prime} W^{\prime}}\).
c. Which side of the image is congruent to side \(\overline{Y Z}\)?
Answer:
∠X is congruent to ∠X’;
∠Y is congruent to ∠Y’;
∠Z is congruent to ∠Z’;
∠W is congruent to ∠W’;
d. Which angle of the image is congruent to ∠X?
Name three other pairs of congruent angles.
Answer:
Question 9.
Critical Thinking Is it possible that the image of a point after a reflection could be the same point as the preimage? Explain.
Answer:
Yes, it’s possible when the point is on the line of the reflection. Distance between the point and the line is 0, and the image of the point will be on the same place like the preimage.
H.O.T. Focus on Higher Order Thinking
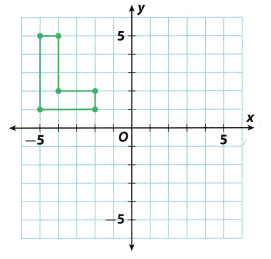
Question 10.
a. Graph the image of the figure shown after a reflection across the y-axis.
Answer:
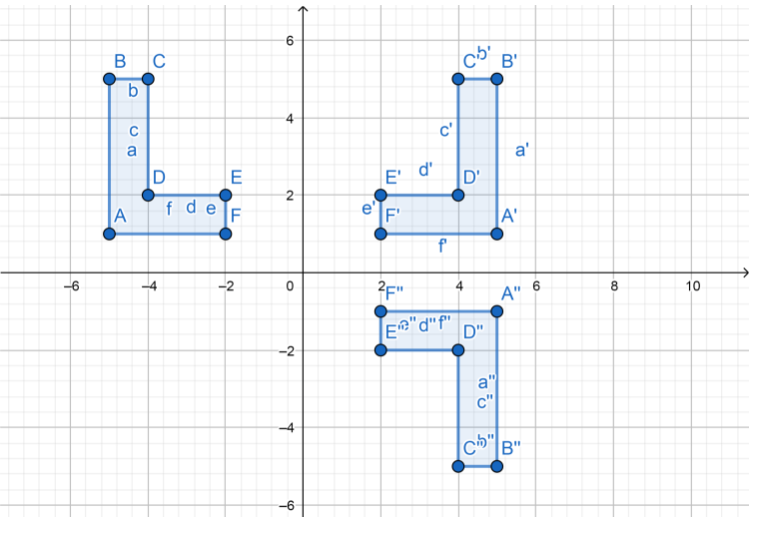
b. On the same coordinate grid, graph the image of the figure you drew in part a after a reflection across the x-axis.
Answer:

c. Make a Conjecture What other sequence of transformations would produce the same final image from the original preimage? Check your answer by performing the transformations. Then make a conjecture that generalizes your findings.
Answer:
With a reflection of the figure first across the x-axis, and then over the y-axis, it’s obtained the same image of the original figure.
Question 11.
a. Graph triangle DEF with vertices D(2, 6), E(5, 6), and F(5, 1) on the coordinate grid.
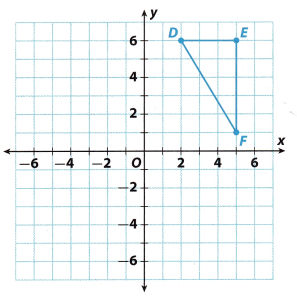
Answer:
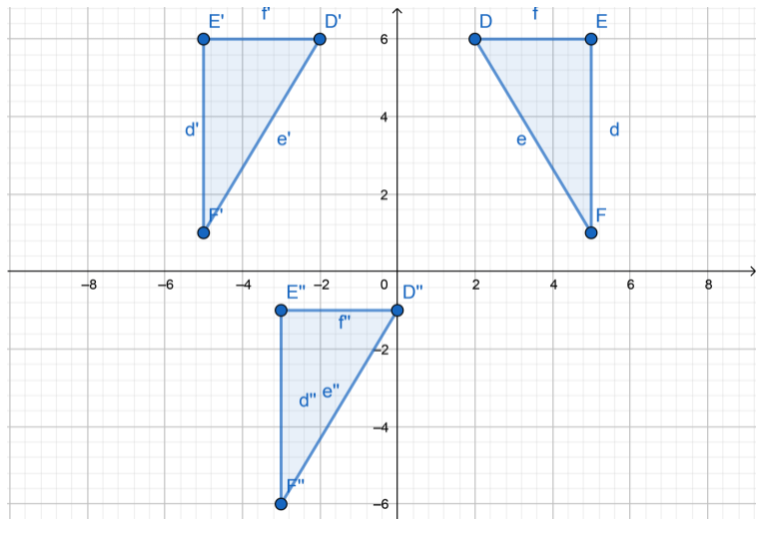
b. Next graph triangle D’E’F’, the image of triangle DEF after a reflection across the y-axis.
Answer:

c. On the same coordinate grid, graph triangle D”E”F”, the image of triangle D’E’F’ after a translation of 7 units down and 2 units to the right.
Answer:
After a translation of 7 units down and 2 units to the Left and a refLection across the y-axis we can get triangle D’E’F’, the image of triangle DEF.
d. Analyze Relationships Find a different sequence of transformations that will transform triangle DEF to triangle D”E”F”.
Answer: