Texas Go Math Grade 8 Unit 1 Study Guide Review Answer Key

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Unit 1 Study Guide Review Answer Key.

Texas Go Math Grade 8 Unit 1 Study Guide Review Answer Key

Texas Go Math Grade 8 Unit 1 Exercises Answer Key

Find the two square roots of each number. If the number is not a perfect square, approximate the values to the nearest 0.05. (Lesson 1.1)

Module 1 Real Numbers

Question 1.
16 ___________
Answer:
\(\sqrt{16}\) = 4, since 4 . 4 = 16
–\(\sqrt{16}\) = -4, since (-4) . (-4) = 16
Two square roots of 16 are +4 and -4.

Question 2.
\(\frac{4}{25}\) _______________
Answer:

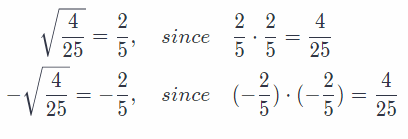
Two square roots of \(\frac{4}{25}\) are +\(\frac{2}{5}\) and –\(\frac{2}{5}\)

Question 3.
225 _________
Answer:
\(\sqrt{225}\) = 15, since 15 . 15 = 225
–\(\sqrt{225}\) = -15, since (-15) . (-15) = 225
Two square roots of 225 are +15 and -15.

Question 4.
\(\frac{1}{49}\) _______________
Answer:

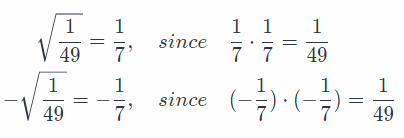
Two square roots of \(\frac{1}{49}\) are +\(\frac{1}{7}\) and –\(\frac{1}{7}\)

Question 5.
\(\sqrt{10}\) _______
Answer:
Since 10 is not a perfect square, approximate 10 with two closest perfect squares:
9 < 10 < 1.6
Take square root to find in between what numbers lies \(\sqrt{10}\):
\(\sqrt{9}\) < \(\sqrt{10}\) < \(\sqrt{16}\)
Solve:
3 < \(\sqrt{10}\) < 4
We now know that \(\sqrt{10}\) lies between 3 and 4 but since 10 is closer to 9, \(\sqrt{10}\) is closer to 3. To find a better approximation pick a few number between 3 and 4 but closer to 3 and square them to see where they lie relating to 10:
3.10² = 9.61 < 10
3.15² ≈ 9.92 < 10
3.2² = 10.24 > 10
We see that 3.15² is closer to 10 than 3.2² so we can conclude that the best approximation to the nearest 0.05 is 3.15

Question 6.
\(\sqrt{18}\) _______
Answer:
Since 18 is not a perfect square, approximate 18 with two closest perfect squares:
16 < 18 < 25
Take square root to find in between what numbers lies \(\sqrt{18}\):
\(\sqrt{16}\) < \(\sqrt{18}\) < \(\sqrt{25}\)
Solve:
4 < \(\sqrt{18}\) < 5
We now know that \(\sqrt{18}\) lies between 4 and 5 but since 18 is closer to 16, \(\sqrt{18}\) is closer to 4. To find a better approximation pick a few number between 4 and 5 but closer to 4 and square them to see where they lie relating to 18:
4.15² ≈ 17.22 < 18
4.2² = 17.64 < 18 4.25 ≈ 18.06 > 18
We see that 4.25² is closer to 18 than 4.2² so we can conclude that the best approximation to the nearest 0.05 is 4.25

Write all names that apply to each number. (Lesson 1.2)

Question 7.
\(\frac{2}{3}\) _______________
Answer:
Since \(\frac{2}{3}\) isn’t an integer or a whole number but is expressed as a ratio of two integers we can conclude that it is a rational, real number.

Rational, real.

Question 8.
–\(\sqrt{100}\) _______
Answer:
–\(\sqrt{100}\)
-10
Rational, integer, real

Question 9.
\(\frac{15}{5}\) _______________
Answer:
Since \(\frac{15}{5}\) is a ratio of two integers it is a rational real number. But, since
\(\frac{15}{5}\) = 3
it is also an integer and a whole number.

Whole, integer, rational, real

Question 10.
\(\sqrt{21}\) _______
Answer:
\(\sqrt{21}\)
Irrational, real

Compare. Write <, >, or . (Lesson 1.3)

Question 11.

Answer:
\(\sqrt{7}\) + 5 ? 7 + \(\sqrt{5}\) Given
\(\sqrt{7}\) is between 2 and 3 Estimate the value of \(\sqrt{7}\)
\(\sqrt{5}\) is between 2 and 3 Estimate the value of \(\sqrt{5}\)
\(\sqrt{7}\) + 5 is between 7 and 8 Use approximations to simply the expressions
7 + \(\sqrt{5}\) is between 9 and 10
\(\sqrt{7}\) + 5 < 7+ \(\sqrt{5}\) Compare

Question 12.

Answer:
6 + \(\sqrt{8}\) ? \(\sqrt{6}\) + 8 Given
\(\sqrt{8}\) is between 2 and 3 Estimate the value of \(\sqrt{8}\)
\(\sqrt{6}\) is between 2 and 3 Estimate the value of \(\sqrt{6}\)
6 + \(\sqrt{8}\) is between 8 and 9 Use approximations to simply the expressions
\(\sqrt{6}\) + 8 is between 10 and 11
6 + \(\sqrt{8}\) < \(\sqrt{6}\) + 8 Compare

Question 13.

Answer:
\(\sqrt{4}\) – 2 ? 4 – \(\sqrt{2}\) Given
\(\sqrt{4}\) = 2 Estimate the value of \(\sqrt{4}\)
\(\sqrt{2}\) is between 1 and 2 Estimate the value of \(\sqrt{2}\)
\(\sqrt{4}\) – 2 = 2 – 2 = 0 Use approximations to simply the expressions
4 – \(\sqrt{2}\) is between 3 and 2
\(\sqrt{4}\) – 2 < 4 – \(\sqrt{2}\) Compare

Order the numbers from least to greatest. (Lesson 1.3)

Question 14.
\(\sqrt{81}\), \(\frac{72}{7}\), 8.9
Answer:
First, express au. numbers in (simplified) decimal form so we could easily compare them.
\(\sqrt{81}\) = 9 Simplify (81 is a perfect square)
\(\frac{72}{7}\) = 10.29 Using long division divide 72 by 7
8.9 Already in the simplest form
Now we can compare:
8.9 < 9 < 10.26 (1)
From (1) it now follows that:
From least to greatest: 8.9 < \(\sqrt{81}\) < \(\frac{72}{7}\)

Question 15.
\(\sqrt{7}\), 2.55, \(\frac{7}{3}\)
Answer:
\(\sqrt{7}\) lies between 2 and 3 Estimate the value of \(\sqrt{7}\)
Since $7$ is approximately midway
between $4$ and $9$, hence
2.65² = 6.50
2.6² = 6.76
2.65² = 7.02
Since $2.65^{2} = 7.02$ $\sqrt{7}
\approx 2.65$

2.55 Given

\(\frac{7}{3}\) = 2.33 Divide 7 by 3

Graph on the number line

\(\frac{7}{3}\), 2.55, \(\sqrt{7}\)

Module 2 Scientific Notation

Essential Question
How can you use scientific notation to solve real-world problems?
Answer:
Scientific notation is used to write very large or very small numbers using fewer digits. See how scientists use this notation to describe astronomical distances, such as the distance between planets, or microscopic distances, such as the length of a blood cell

Exercises
Write each number in scientific notation. (Lessons 2.1, 2.2)

Question 1.
3000 _________
Answer:
3000 in the scientific notation is 3 × 10³
Here move the decimal 3 times to the left then it is 3. But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.

Question 2.
0.000015 _____
Answer:
0.000015 in the scientific notation is 1.5 × 10^-5.
Here move the decimal 5 times to the left then it is 1.5. But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is negative.

Question 3.
25,500,000 _____
Answer:
25,500,000 Given
2.55 Move the decimal point 7 places to the left. Remove the extra zeros.
10, 000, 000 Divide the original number by the result from above.
10⁷ Write the answer as power of 10.
2.55 × 10⁷ Write the product of the resuLts from step 1 and 2
2.55 × 10⁷

Question 4.
0.00734 _________
Answer:
0.00734 Given
7.34 Place the decimal point
3 Count the number of places the decimal point is moved.
7.34 × 10^-3 Multiply 7.34 times a power of 10. Since 0.00734 is less than 1, the decimal point moves to the right and the exponent on 10 is negative.
7.34 × 10^-3

Write each number in standard notation. (Lessons 2.1, 2.2)

Question 5.
5.23 × 10⁴ __________________________
Answer:
5.23 × 10⁴ Given
4 Use the exponent of the power of 10 to determine the number paces to move the decimal point
places
52,300 Place the decimal point Since you are going to write a number greater than 5.23, move the decimal point to the right. Add placeholder zeros if necessary.
52,300

Question 6.
1.05 × 10⁶ __________________________
Answer:
Given that 1.05 × 10⁶
10⁶ = 1000000
1.05 × 1000000 = 1050000.

Question 7.
4.7 × 10^-1 __________________________
Answer:
Given that 4.7 × 10^-1.
10^-1 = 0.1
4.7 × 0.1 = 0.47.

Question 8.
1.33 × 10^-5 __________________________
Answer:
1.33 × 10^-5 Given
5 Use exponent of the power of 10 to determine the number paces to move the decimal point
places
0.0000133 Place the decimal point Since you are going to write a number greater than 1.33, move decimal point to the right. Add placeholder zeros if necessary.
0.0000133

Use the information in the table to write each weight in scientific notation. (Lessons 2.1, 2.2)

Question 9.
Ant _________
Answer:
Given that the weight of the ant = 0.000000661.
0.000000661 in the scientific notation is 6.61 × 10^-7.
Here move the decimal 7 times to the left then it is 6.61. But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is negative.

Question 10.
butterfly _________
Answer:
Given that the weight of the butterfly = 0.00000625.
0.00000625 in the scientific notation is 6.25 × 10^-6.
Here move the decimal 6 times to the left then it is 6.25. But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is negative.

Question 11.
elephant _________
Answer:
Given that the weight of the elephant = 9900
9900 in the scientific notation is 9.9 × 10³
Here move the decimal 3 times to the left then it is 9.9.But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is positive.

Texas Go Math Grade 8 Unit 1 Performance Tasks Answer Key

Question 1.
Careers In Math Astronomer An astronomer is studying Proxima Centauri, which is the closest star to our Sun. Proxima Centauri is 39,900,000,000,000,000 meters away.
a. Write this distance in scientific notation.
Answer:
39,900,000,000,000,000 Distance in meters
3.99 Move the decimal point 16 places to the left. Remove the extra zeros
10, 000, 000, 000, 000, 000 Divide the original number by the result from Step 1. Write the answer as power of 10.
10¹⁶
3.99 × 10¹⁶ Write the product of the results from the above

b. Light travels at a speed of 3.0 × 10⁸ m/s (meters per second). How can you use this information to calculate the time in seconds it takes for light from Proxima Centauri to reach Earth? How many seconds does it take? Write your answer in scientific notation.
Answer:
speed = 3.0 × 10⁸ speed in meters per second

\(\frac{3.99}{3}\) = 1.33 Find the quotient by dividing the decimals and using the laws of exponents
\(\frac{10^{16}}{10^{8}}\) = 10^16-8 = 10⁸
1.33 × 10⁸ Combine the answers to write the distance in scientific notation
It takes $1.33 \times 10^{8}$ seconds
for the light to reach Earth

c. Knowing that 1 year = 3.1536 × 10⁷ seconds, how many years does it take for light to travel from Proxima Centauri to Earth? Write your answer in standard notation. Round your answer to two decimal places.
Answer:
1.33 × 10⁸ seconds From part b
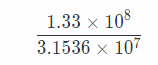1 yr = 3.1536 × 10⁷

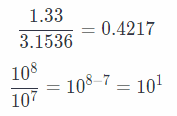
Find the quotient by dividing the decimals and using the Laws of exponents
0.4217 × 10¹ combine the answers to write the distance in scientific notation
4.22 Write in standard notation
It takes $4.22$ years for the light to reach Earth

Question 2.
Cory is making a poster of common geometric shapes. He draws a square with a side length of 4³ cm, an equilateral triangle with a height of \(\sqrt{200}\) cm, a circle with a circumference of 8π cm, a rectangle with length \(\frac{122}{5}\) cm, and a parallelogram with base 3.14 cm.

a. Which of these numbers are irrational?
Answer:
\(\sqrt{200}\) cm and 8π cm are irrational Irrational numbers are real number that cannot be expressed in the form \(\frac{a}{b}\)

b. Write the numbers in this problem in order from least to greatest. Approximate π as 3.14.
Answer:
4³ = 64 Evaluate the power
\(\sqrt{200}\) Estimate the value of \(\sqrt{200}\)
lies between $14$ and $15$ Since
$200$ is closer to $196 = 14^{2}$,
hence
14.1² = 198.81
14.15² = 200.22
14.2² = 201.64
Since $14.15”{2} = 200.22$
$\sqrt{200} \approx 14.15$
8π = 8 * 3.14 = 25.12 π = 3.14
\(\frac{122}{5}\) = 24.4 Divide 122 by 5
3.14 Given
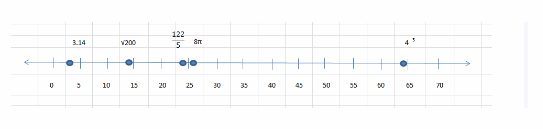Graph on the number line
3.14, \(\sqrt{200}\), \(\frac{122}{5}\), 8π, 4³ From least to greatest

c. Explain why 3.14 is rational, but π is not.
Answer:
3.14 can be expressed in the form \(\frac{a}{b}\) but π cannot be expressed in fraction form. It gives a value which is neither a terminating or repeating decimal.

3.14 is rational but π is not

Texas Go Math Grade 8 Unit 1 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
A square on a large calendar has an area of 4220 square millimeters. Between which two integers is the length of one side of the square?
(A) between 20 and 21 millimeters
(B) between 64 and 65 millimeters
(C) between 204 and 205 millimeters
(D) between 649 and 650 millimeters
Answer:
(B) between 64 and 65 millimeters

Explanation:
The area of a square is found by multiplying the side of the square by itself. Therefore, to find the side of the
square, we have to take the square root of the area.
Lets denote with A the area of a square of the calendar and with s each side of the square. We have:
A = 4220
A = s • s
s = \(\sqrt{A}\) = \(\sqrt{4220}\)
Following the steps as in “Explore activity 1” on page 9, we can make an estimation for the irrational number:

Therefore, the side of the square is between 64 and 65 millimeters.

Question 2.
Which of the following numbers is rational but not an integer?
(A) -9
(B) -4.3
(C) 0
(D) 3
Answer:
(B) -4.3

Explanation:
-4.3 is not an integer
Integers are whole numbers that can be positive, negative or zero.

Question 3.
Which statement is false?
(A) No integers are irrational numbers.
(B) All whole numbers are integers.
(C) All rational numbers are real numbers.
(D) All integers are whole numbers.
Answer:
(D) All integers are whole numbers.

Explanation:
All integers are whole numbers is false
Whole numbers are non-negative while integers are negative, positive or zeros.

Question 4.
Which set best describes the numbers displayed on a telephone keypad?
(A) whole numbers
(B) rational numbers
(C) real numbers
(D) integers
Answer:
The rational numbers are displayed on the telephone keypad.
Option B is the correct answer.

Question 5.
In 2011, the population of Laos was about 6.586 × 10⁶ people. What is this number written in standard notation?
(A) 6,586 people
(B) 658,600 people
(C) 6,586,000 people
(D) 65,860,000 people
Answer:
(C) 6,586,000 people

Explanation:
6.586 × 10⁶ Population in 2011

6 Use exponent of the power of 10 to determine the number places to move the decimal point
places

6, 586, 000
Place the decimal point Since you are going to write a number greater than 6.586, move decimal point to the right Add placeholder zeros if necessary.
There are 6, 586, 000 people in $2011$

Question 6.
Which of the following is not true?

Answer:
(D) 6 – \(\sqrt{35}\) < 0 Explanation: a. Since both 16 and 4 are perfect squares we can evaluate them easily: and the statement is TRUE. b. We know that π ≈ 3.14 which means that 4π ≈ 4 × 3.14 = 12.56 Obviously, 12.56 > 12
so,
4π > 12
and the statement is TRUE

c. Lets first evaluate \(\sqrt{18}\) and \(\frac{15}{2}\)
Since 18 is not a perfect square find two closest squares that 1 lies in between:
16 < 18 < 25
\(\sqrt{16}\) < \(\sqrt{18}\) < \(\sqrt{25}\)
4 < \(\sqrt{18}\) < 5
Since 18 is closer to 16 a good approximation for \(\sqrt{18}\) is 4 but we are certain that \(\sqrt{18}\) is not larger or equal to 5
To express \(\frac{15}{2}\) as a fraction use long division to divide 15 by 2
\(\frac{15}{2}\) = 7.5
Now we can see that
\(\sqrt{18}\) + 2 < 5 + 2 = 7
\(\frac{15}{2}\) = 7.5
We can conclude that \(\sqrt{18}\) + 2 < \(\frac{15}{2}\)
and the statement is TRUE.

d. Since
6² = 36
36 > 35
by taking square roots from both sides we can see that
\(\sqrt{35}\) < \(\sqrt{36}\) = 6 but now 6 – \(\sqrt{35}\) > 0
It now follows that the statenient is NOT TRUE.

Question 7.
Which number is between \(\sqrt{50}\) and \(\frac{5 \pi}{2}\)?
(A) \(\frac{22}{3}\)
(B) 2\(\sqrt{8}\)
(C) 6
(D) π + 3
Answer:
(A) \(\frac{22}{3}\)

Explanation:
\(\sqrt{50}\) Given
and \(\frac{5 \pi}{2}\)
\(\sqrt{50}\) lies between 7 and 8 Evaluate the value of \(\sqrt{50}\)
7.0² = 49.00
7.05² = 49.70
7.15² = 51.12
Since $7.05^{2} = 49.7$, $\sqrt{50}
\approx 7.05$

\(\frac{5 * 3.14}{2}\) = 7.85 Evaluate \(\frac{5 \pi}{2}\)
The number should be between 7.05 and 7.85
\(\frac{22}{3}\) = 7.33

Question 8.
What number is indicated on the number line?

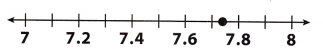
(A) π + 4
(B) \(\frac{152}{20}\)
(C) \(\sqrt{14}\) + 4
(D) \(7 . \overline{8}\)
Answer:
Given that the number \(\sqrt{14}\) + 4 indicated on the number line.
\(\sqrt{14}\) + 4 = 7.7416.
Option C is the correct answer.

Question 9.
Which of the following is the number 5.03 × 10^-5 written in standard form?
(A) 503,000
(B) 50,300,000
(C) 0.00503
(D) 0.0000503
Answer:
The standard form of the number 5.03 × 10^-5
5.03 × 0.00001 = 0.0000503
Here move the decimal 5 times to the left then it is 5.03. But the three are less than 10.
Moved the decimal to the left is the exponent and the exponent is negative.
Option D is the correct answer.

Question 10.
In a recent year, about 20,700,000 passengers traveled by train in the United States. What is this number written in scientific notation?
(A) 2.07 × 10¹ passengers
(B) 2.07 × 10⁴ passengers
(C) 2.07 × 10⁷ passengers
(D) 2.07 × 10⁸ passengers
Answer:
(C) 2.07 × 10⁷ passengers

Explanation:
20,700,000 Given
2.07 Move the decimal point 7 places to the left Remove the extra zeros
10,000,000 Divide the original number by the result from above.
10⁷ Write the answer as power of 10.
Write the product of the results from above
2.07 × 10⁷
There are $2.07 \times 10^{7}$ passengers that travel by train

Question 11.
A quarter weighs about 0.025 pound. What is this weight written in scientific notation?
(A) 2.5 × 10^-2 pound
(B) 2.5 × 10¹ pound
(C) 2.5 × 10^-1 pound
(D) 2.5 × 10² pound
Answer:
(A) 2.5 × 10^-2 pound

Explanation:
We need to express the number 0.025 in scientific notation (a × 10ⁿ, where a is a number greater or equal to 1 but less than 10.
In that spirit we see we need to move the decimal point 2 places (to the right) so the power of 10 needs to be 2
(or -2). Since the given number is a number smaller than 1 the exponent in the power of 10 is going to be negative (-2).
0.025 = 2.5 × 10^-2

Question 12.
Which of the following is the number 3.0205 × 10^-3 written in standard notation?
(A) 0.00030205
(B) 0.0030205
(C) 3.0205
(D) 3020.5
Answer:
The standard form of the number 3.0205 × 10 power of -3 = 0.00030205.
Option A is the correct answer.

Question 13.
A human fingernail has a thickness of about 4.2 × 10^-4 meter. What is this width written in standard notation?
(A) 0.0000042 meter
(B) 0.000042 meter
(C) 0.00042 meter
(D) 0.0042 meter
Answer:
(C) 0.00042 meter

Explanation:
a We are given: 4.2 × 10^-4 meter Since the power of 10 is a negative 4 we need to move the decimal place 4
places to the left to get a number written in scientific notation.
4.2 × 10^-4 meter = 0.00042 meter Move decimal point and add placeholder zeros

b. Since 1 meter = 0.001 millimeter or 1 millimeter = 10³ meter we can calculate how many millimeters is 4.2 × 10^-4 meter
4.2 × 10^-4 meter = (4.2 × 10^-4) × 10³ millimeter = 0.42 millimeter
We can conclude that their measurements agree.

c. Since the thickness of a human fingernail is a very small number it is more appropriate to express it in milimeters than in meters (because a millimeter is 1000 times smaller than a meter).

Gridded Response

Question 14.
The square root of a number is -18. What is the other square root?

Answer:
A square root always has 2 numbers, one is positive and other is negative.
So, one number is -18 and the other number is 18

Hot Tip!
Underline key words given in the test question so you know for certain what the question is asking.

Question 15.
Jerome is writing a number in scientific notation. The number is greater than one million and less than ten million. What will be the exponent in the number Jerome writes?

Answer:
Given that Jerome is writing the number in the scientific notation.
The number is greater than one million and less than ten million.
The exponent in the number is
1 million = 10⁶
10 million = 10⁷
The number is > 10⁶ < 10⁷
The exponent number is 6.

Question 16.
Write the number 3.3855 × 10² in standard notation.

Answer:
3.3855 × 10² in the standard form is 3.3855 × 100 = 338.55

Texas Go Math Grade 8 Unit 1 Vocabulary Preview Answer Key

Use the puzzle to preview key vocabulary from this unit. Unscramble the circled letters to answer the riddle at the bottom of the page.

Question 1.
TCREEFP
SEAQUR

Answer:
PERFECT
SQUARE

Question 2.
NOLRATAI
RUNMEB

Answer:
RATIONAL
NUMBER

Question 3.
PERTIANEG
MALCEDI

Answer:
PERTAINGE
DECIMAL

Question 4.
LAER
SEBMNUR

Answer:
REAL
NUMBERS

Question 5.
NIISICFTCE
OITANTON

Answer:
SCIENTIFIC
NOTATION

1. Has integers as its square roots. (Lesson 1-1)
2. Any number that can be written as a ratio of two integers. (Lesson 1-1)
3. A decimal in which one or more digits repeat infinitely. (Lesson 1-1)
4. The set of rational and irrational numbers. (Lesson 1-2)
5. A method of writing very large or very small numbers by using powers of 10. (Lesson 2-1)

Q: What keeps a square from moving?
A: ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___!
Answer:
SQUARE ROOTS