Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 7 Quiz Answer Key.
Texas Go Math Grade 8 Module 7 Quiz Answer Key
Texas Go Math Grade 8 Module 7 Ready to Go On? Answer Key
7.1 Parallel Lines Cut b a Transversal
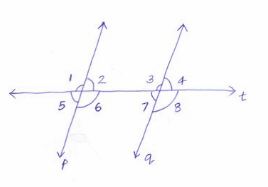
In the figure, line P|| line q. Find the measure of each angle if m∠8 = 115°.
Question 1.
m∠7 = ______________
Answer:
According to the Exterior Angle Theorem, we have:
m∠7 + m∠8 = 180°
m∠7 + 115° = 180°
m∠7 + 115° – 115° = 180° – 115°
m∠7 = 65°
Question 2.
m∠6 = ______________
Answer:

In the given figure, line P is parallel to line q. So, the angles given in line P is equal to the angles in line q.(corresponding angles)
so, m∠8 is parallel to m∠6
or m∠8 = m∠6 = 115°
Question 3.
m∠1 = ______________
Answer:
this is the given figure of the question
taking a section of a figure, we have
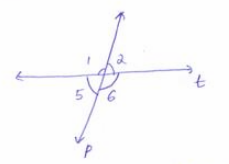
In the previous question, we got m∠6 = 115°
In the figure, ∠1 and ∠6 are alternate exterior angles
so, m∠1 = m∠6 = 115°
7.2 Angle Theorems for Triangles
Find the measure of each angle.
Question 4.
m∠A = ______________
Answer:
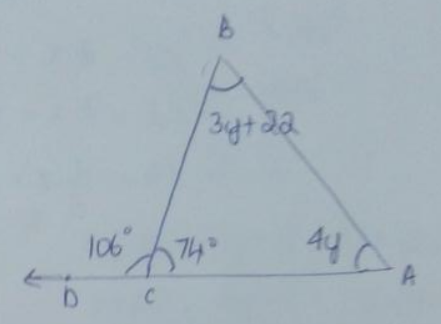
From the triangle sum theorem
sum of the angles of triangle is 180°
m∠A + m∠B + m∠C = 180°
4y + (3y + 22) + 74° = 180°
7y = 180 – 96 = 84
y = 12°
m∠A = 4y = 4 × 12 = 48°
and m∠B = 3y + 22 = 3 × 12 + 22
= 58°
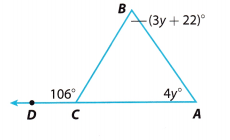
Question 5.
m∠B = ________
Answer:
Using the Exterior Angle Theorem we have:
m∠A + m∠B = m∠BCD
We substitute the given angle measures and we solve the equation for y.
(4y)° + (3y + 22)° = 106°
4y° + 3y° + 22° = 106°
7y° + 22° = 106°
7y° + 22° – 22° = 106° – 22°
7y° = 84°
\(\frac{7 y^{\circ}}{7^{\circ}}\) = \(\frac{84^{\circ}}{7^{\circ}}\)
y = 12
We use the value of y to find m∠B.
m∠B = (3y + 22)° = (3 . 12 + 22)° = 58°
m∠B = 58°
Question 6.
m∠BCA = ________
Answer:
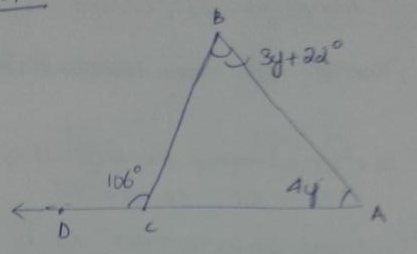
In the given triangle,
m∠A = 4y m∠B = 3y + 22°
and m∠BCD = 106°
using exterior angle theorem
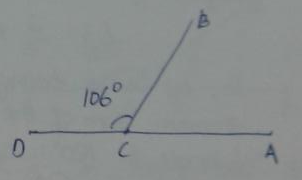
m∠BCD + m∠BCA = 180°
m∠BCA = 180° – 106°
= 74°
So, m∠BCA = 74°
∠BCA = 74 degrees
7.3 Angle-Angle Similarity
Triangle FEG is similar to triangle IHJ. Find the missing values.
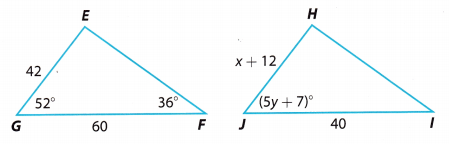
Question 7
x = ________
Answer:
In similar triangles, corresponding side lengths are proportional
\(\frac{H J}{E G}\) = \(\frac{I J}{F G}\)
\(\frac{x+12}{42}\) = \(\frac{40}{60}\)
\(\frac{x+12}{42}\) = \(\frac{4}{6}\)
6 . 42 . \(\frac{x+12}{42}\) = \(\frac{4}{6}\) . 6 . 42
6(x + 12) = 168
6x + 72 = 168
6x + 72 – 72 = 168 – 72
6x = 96
\(\frac{6 x}{6}\) = \(\frac{96}{6}\)
x = 16
Question 8.
y = ________
Answer:
In similar triangles, corresponding angles are congruent
m∠HJI = m∠EGF
(5y + 7)° = 52°
5y + 7° = 52°
5y° + 7° – 7° = 52° – 7°
5y° = 45
\(\frac{5 y^{\circ}}{5^{\circ}}\) = \(\frac{45^{\circ}}{5^{\circ}}\)
y = 9
Question 9.
m∠H = ___
Answer:
From the Triangle Sum Theorem we have:
m∠E + m∠F + m∠G = 180°
We substitute the given angle measures and we solve for m∠E.
m∠E + 36° + 52° = 180°
m∠E + 88° = 180°
m∠E + 88° – 88° = 180° – 88°
m∠E = 92°
In similar triangles, corresponding angles are congruent. Therefore,
m∠H = m∠E
m∠H = 92°
Essential Question
Question 10.
How can you use similar triangles to solve real-world problems?
Answer:
We know that if two triangles are similar, then their corresponding angles are congruent and the lengths of their
corresponding sides are proportional. We can use this to determine values that we cannot measure directly. For example, we can calculate the length of the tree if we measure its shadow and our shadow in a sunny day.
Texas Go Math Grade 8 Module 7 Mixed Review Texas Test Prep Answer Key
Selected Response
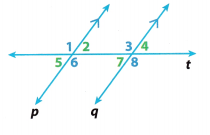
Use the figure for Exercises 1 and 2.
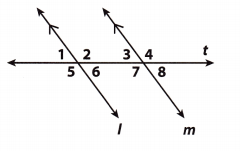
Question 1.
Which angle pair is a pair of alternate exterior angles?
(A) ∠5 and ∠6
(B) ∠6 and ∠7
(C) ∠5 and ∠4
(D) ∠5 and ∠2
Answer:
(C) ∠5 and ∠4
Explanation:
∠5 and ∠4 are alternate exterior angles
Question 2.
Which of the following angles is not congruent to ∠3?
(A) ∠1
(B) ∠2
(C) ∠6
(D) ∠8
Answer:
(B) ∠2
Explanation:
∠2 and ∠3 are same-side interior angles. They are not congruent; instead their sum is equal to 180°
Question 3.
The measures of the three angles of a triangle are given by 2x + 1, 3x – 3, and 9x. What is the measure of the smallest angle?
(A) 13°
(B) 27°
(C) 36°
(D) 117°
Answer:
(B) 27°
Explanation:
From the Triangle Sum Theorem we have:
m∠1 + m∠2 + m∠3 = 180°
We substitute the given angle measures and we solve for X.
(2x + 1)° + (3x – 3)° + (9x)° = 180°
2x° + 1 + 3x° – 3° + 9x° = 180°
14x° – 2° = 180°
14x° – 2° + 2° = 180° + 2°
14x° = 178°
\(\frac{14 x^{\circ}}{14^{\circ}}\) = \(\frac{182^{\circ}}{14^{\circ}}\)
x = 13
We use the value of x to find m∠1, m∠2 and m∠3.
m∠1 = (2x + 1)° = (2 . 13 + 1)° = 27°
m∠1 = 27°
m∠2 = (3x – 3)° = (3 . 13 – 3)° = 36°
m∠2 = 36°
m∠3 = (9x)° = (9 . 13)° = 117°
m∠3 = 117°
The smallest angle is 27°
Question 4.
Which is a possible measure of ∠DCA in the triangle below?
(A) 36°
(B) 38°
(C) 40°
(D) 70°
Answer:
(D) 70°
Explanation:
Using the Exterior Angle Theorem we have:
m∠A + m∠B = m∠DCA
m∠A + 40° = m∠DCA
As we can see, m∠DCA will be greater than 40°. The only suitable option is D, 70°.
Question 5.
Kaylee wrote in her dinosaur report that the Jurassic period was 1.75 × 108 years ago. According to Kaylee’s report, how many years ago was the Jurassic period?
(A) 1,750,000
(B) 17,500,000
(C) 175,000,000
(D) 17,500,000,000
Answer:
(C) 175,000,000
Explanation:
The Jurassic period was 1.75 × 108 years ago. In standard form
108 = 100, ooo, 000 (Ten with eight zeros) (1)
1.75 × 108 = 1.75 × 100, 000,000 (Substitute) (2)
= 175,000,000 (3)
Correct answer is C 175, 000, 000
Question 6.
Given that y varies directly with x, what is the equation of direct variation if y is 16 when x is 20?
(A) y = 1\(\frac{1}{5}\)x
(B) y = \(\frac{5}{4}\)x
(C) y = \(\frac{4}{5}\)x
(D) y = 0.6x
Answer:
(C) y = \(\frac{4}{5}\)x
Explanation:
Given that y is proportional to x, and if y is 16, and x is 20 we can write proportion
\(\frac{y}{x}\) = \(\frac{16}{20}\) (1)
\(\frac{y}{x}\) = \(\frac{4}{5}\)x (simplify the fraction) (2)
x × \(\frac{4}{5}\) = \(\frac{4}{5}\) × x (Use properties of equality to get y by itself.) (3)
y = \(\frac{4}{5}\)x (4)
Correct answer is C
Gridded Response
Question 7.
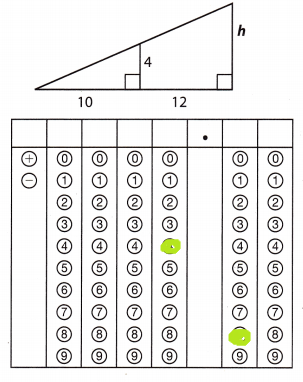
What is the value of h in the triangle below?
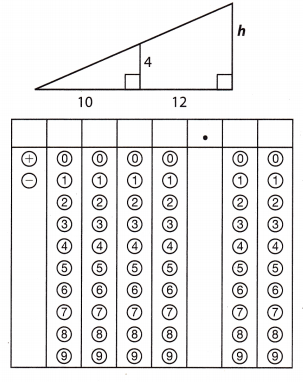
Answer:
In similar triangles the corresponding sides and lengths are proportional.
4/10 = h/12
4 × 12 = h × 10
48/10 = h
h = 4.8