Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 7.3 Answer Key Using Ratios and Rates to Solve Problems.
Texas Go Math Grade 6 Lesson 7.3 Answer Key Using Ratios and Rates to Solve Problems
Reflect
Question 1.
Explain the Error Marisol makes the following claim: “Bailey’s lemonade is stronger because it has more lemonade concentrate. Bailey’s lemonade has 3 cups of lemonade concentrate, and Anna’s lemonade has only 2 cups of lemonade concentrate” Explain why Marisol is incorrect.
Answer:
The strength of the Lemonade also depends on the amount of water
Question 2.
In the science club, there are 2 sixth graders for every 3 seventh graders. At this year’s science fair, there were 7 projects by sixth graders for every 12 projects by seventh graders. Is the ratio of sixth graders to seventh graders in the science club equivalent to the ratio of science fair projects by sixth graders to projects by seventh graders? Explain.
Answer:
The ratio of sixth-graders to seventh-graders in the science club is given by 2 : 3 or \(\frac{2}{3}\)
Reflect
Question 3.
In fifteen minutes, Lena can finish 2 math homework problems. How many math problems can she finish in 75 minutes? Use a double number line to find the answer.
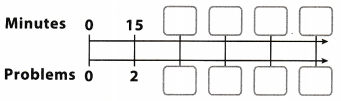
Answer:
Find the unit rate. How long does Leny need to solve the problem?
Divide to find the unit rate
\(\frac{15 \text { minutes }}{2 \text { problems }}=\frac{7.5 \text { minutes }}{1 \text { problems }}\)
Lena solves one prob1em in 7.5 minutes
Divide
75 minutes ÷ 7.5 minutes = 10 problems
In 75 minutes, Lena solves 10 problems
Final solution = 10
Texas Go Math Grade 6 Lesson 7.3 Guided Practice Answer Key
Question 1.
Celeste is making fruit baskets for her service club to take to a local hospital. The directions say to fill the boxes using 5 apples for every 6 oranges. Celeste is filling her baskets with 2 apples for every 3 oranges.
a. Complete the tables to find equivalent ratios.

Answer:

b. Compare the ratios. Is Celeste using the correct ratio of apples to oranges?
Answer:
No, Celeste is not using the correct ratio of apples to oranges. It can be seen that when there are 6 oranges in the 2nd table, there are 4 apples white the direction is of 5 apples.
Question 2.
Neha used 4 bananas and 5 oranges in her fruit salad. Daniel used 7 bananas and 9 oranges. Did Neha and Daniel use the same ratio of bananas to oranges? If not, who used the greater ratio of bananas to oranges?
Answer:
The ratio of bananas to oranges is Neha’s salad is 4 : 5 or \(\frac{4}{5}\) = 0.8.
The ratio of bananas to oranges is Daniel’s salad is 7 : 9 or \(\frac{7}{9}\) = 0.\(\overline{7}\)
Since 0.8 > 0. bar 7, it can be said that the banana to oranges ratio was more in Neha’s salad
Banana to oranges ratio was more in Neha’s salad.
Question 3.
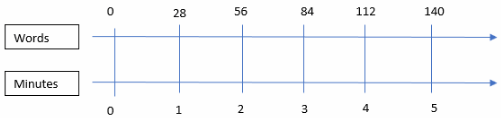
Tim is a first grader and reads 28 words per minute. Assuming he maintains the same rate, use the double number line to find how many words he can read in 5 minutes.
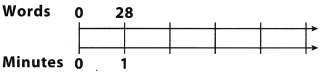
Answer:
He can read 140 words in 5 minutes.
Question 4.
A cafeteria sells 30 drinks every 15 minutes. Predict how many drinks the cafeteria sells every hour.
Answer:
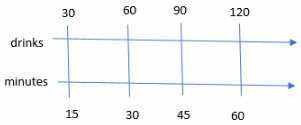
120 drinks are sold every hour.
Essential Question Check-In
Question 5.
Explain how to compare two ratios.
Answer:
Decimal value: The decimal value of the 2 given ratios is evaluated and their values are compared. If the decimal value of both is equal then this implies that they are equivalent, otherwise not.
Same denominator: The 2 given ratios are converted to an equivalent denominator and then their numerators are compared. If the numerators are equal, then this implies that they are equivalent, otherwise not.
Comparing the decimals values or using the same denominator method
Question 6.
Last week, Gina’s art teacher mixed 9 pints of red paint with 6 pints of white paint to make pink. Gina mixed 4 pints of red paint with 3 pints of white paint to make pink.
a. Did Gina use the same ratio of red paint to white paint as her teacher? Explain.
Answer:
To compare this to ratios, find the decjmaL value of both fractions.
Gina’s teacher:
\(\frac{9}{6}=\frac{3}{2}\) = 1.5
Gina:
\(\frac{4}{3}\) = 1.33
They did not use the same ratio of red to white paint
b. Yesterday, Gina again mixed red and white paint and made the same amount of paint, but she used one more pint of red paint than she used last week. Predict how the new paint color will compare to the paint she mixed last week.
Answer:
To compare this to ratios, find the decimal value of both fraction&
Gina’s last week:
\(\frac{4}{3}\) = 1.33
Gina’s current week:
\(\frac{5}{3}\) = 1.33
The new paint has more red paint.
Question 7.
The Suarez family paid $15.75 for 3 movie tickets. How much would they have paid for 12 tickets?
Answer:
Given rate is $ 15.75 for 3 movie tickets. This implies that the cost of 1 ticket is \(\frac{15.75}{3}\) = $5.25. Therefore the cost of 12 tickets will be 12 × $5.25 = $63.
Suarez family will have to pay $63 for 12 tickets.
Question 8.
A grocery store sells snacks by weight. A six-ounce bag of mixed nuts costs $3.60. Predict the cost of a two-ounce bag.
Answer:
Given rate is $:3.60 for 6 ounces bag. This implies that the cost of 1 ounce of snacks is \(\frac{3.60}{6}\) = $ 0.60. Therefore, the cost of 2 ounces will be 2 × $ 0.6 = $ 1.20
The cost of the 2-ounce bag is $1.20
Question 9.
The Martin family’s truck gets an average of 25 miles per gallon. Predict how many miles they can drive using 7 gallons of gas.
Answer:
Given rate is 25 miles per gallon so the truck will travel 25 × 7 = 175 miles on 7 gallons of gas.
The truck will travel 175 miles on 7 gallons of gas.
Question 10.
Multistep The table shows two cell phone plans that offer free minutes for each given number of paid minutes used. Pablo has Plan A and Sam has Plan B.
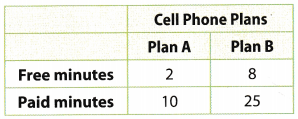
a. What is Pablo’s ratio of free to paid minutes? Cell Pl
Answer:
Pablo’s ratio of free to paid minutes is 2 : 10 or \(\frac{2}{10}\) = 0.2
b. What is Sam’s ratio of free to paid minutes? ________
Answer:
Sam’s ratio of free to paid minutes is 8: 25 or \(\frac{8}{25}\) = 0.32
c. Does Pablo s cell phone plan offer the same ratio of free to paid minutes as Sam’s? Explain.
Answer:
It can be seen that 0.2 ≠ 0.32 this implies that the 2 ratios are not equivalent and that Pablo’s cell phone plan does not offer the same ratio of free to paid minutes as Sam’s.
Question 11.
Consumer Math A store has apples on sale for $3.00 for 2 pounds.
a. If an apple is approximately 5 ounces, how many apples can you buy for $9? Explain.
Answer:
There are 16 ounces in 1 pound.
For $9 dollars we can buy
3. $3 = $9 ⇒ 3. 2 pounds = 6 pounds
Therefore, 6 pounds equals to
6 ∙ 16 = 96 ounces
If an apple is approximately 5 ounces,
\(\frac{96}{5}\) = 19.2
We can buy 19 apples.
b. If Dabney paid less per pound for the same number of apples at a different store, what can you predict about the total cost of the apples?
Answer:
The price of the apples at the other store will be cheaper.
Question 12.
Sophie and Eleanor are making bouquets using daisies and tulips. Each bouquet will have the same total number of flowers. Eleanor uses fewer daisies in her bouquet than Sophie. Whose bouquet will have the greater ratio of daisies to total flowers? Explain.
Answer:
If Eleanor uses fewer daisies, that means she uses more tulips. Therefore, hers bouquet will have the greater ratio of daisies to total flowers (both ratios have the same denominator (number of total flowers) but Eleanor’s has greater denominator).
Question 13.
A town in east Texas received 10 inches of rain in two weeks. If it kept raining at this rate for a 31-day month, how much rain did the town receive?
Answer:
There are 7 days in a week so the given rate becomes \(\frac{10}{14}\) inches per day. This means that in 31 days, it would have rained \(\frac{10}{14}\) × 31 = 22.143 inches.
The town received 22.143 inches of rain in the month.
Question 14.
One patterned blue fabric sells for $15.00 every two yards, and another sells for $37.50 every 5 yards. Do these fabrics have the same unit cost? Explain.
Answer:
The unit cost of the first fabric is \(\frac{\$ 15}{2}\) = $ 7.50 per yard.
The unit cost of the second fabric is \(\frac{\$ 37.5}{5}\) = $ 7.50 per yard.
It can be seen that the unit cost of both the fabrics is same and equal to $7.50 per yard.
These fabrics have the same unit cost.
H.O.T. Focus On Higher Order Thinking
Question 15.
Problem Solving Complete each ratio table.

Answer:
Table a: The table is completed using the ratio \(\frac{24}{18}\) = \(\frac{4}{3}\)
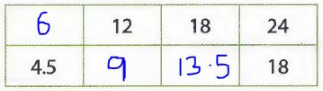
Table b: The table is completed using the ratio \(\frac{40.4}{512}\)

Question 16.
Represent Real-World Problems Write a real-world problem that compares the ratios 5to 9 and 12 to 15.
Answer:
Juice A is made of 5 cups of concentrate mixed with 9 cups of water whiLe Juice B is made of 12 cups of concentrate mixed with 15 cups of water Which of the 2 is more concentrated?
Question 17.
Analyze Relationships Explain how you can be sure that all the rates you have written on a double number line are correct.
Answer:
A double number line consists of 2 different quantities on both sides of the double number line. It can be seen that the a double number line is made correctly by checking the interval between each successive entry on both sides of the number line. This interval should be constant.