Texas Go Math Grade 8 Lesson 9.3 Answer Key Volume of Spheres

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 9.3 Answer Key Volume of Spheres.

Texas Go Math Grade 8 Lesson 9.3 Answer Key Volume of Spheres

Texas Go Math Grade 8 Lesson 9.3 Explore Activity Answer Key

Modeling the Volume of a Sphere

A sphere is a three-dimensional figure with all points the same distance from the center. The radius of a sphere is the distance from the center to any point on the sphere.

You have seen that a cone fills \(\frac{1}{3}\) of a cylinder of the same radius and height h. If you were to do a similar experiment with a sphere of the same radius, you would find that a sphere fills \(\frac{2}{3}\) of the cylinder. The cylinder’s height is equal to twice the radius of the sphere.

Reflect

Question 1.
Analyze Relationships A cone has a radius of r and a height of 2r. A sphere has a radius of r. Compare the volume of the sphere and cone.
Answer:
The volume of the cone with radius of r and a height of 2r is
V_cone = \(\frac{1}{3}\)πr²h
V_cone = \(\frac{1}{3}\) ∙ π ∙ r² ∙ (2r)
V_cone = \(\frac{2}{3}\) ∙ π ∙ r³
The volume of the sphere with radius of r is
V_sphere = \(\frac{4}{3}\)πr³
As we can see, the volume of the sphere is twice the volume of the cone.

Example 1

Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Your Turn

Find the volume of each sphere. Round your answers to the nearest tenth. Use 3.14 for π.

Question 2.
A sphere has a radius of 10 centimeters. __________________
Answer:
It is given that the radius of the sphere is 10 centimeters. Therefore, the volume of the sphere is:
V_sphere = \(\frac{4}{3}\)πr³
V_sphere = \(\frac{4}{3}\) ∙ (3.14) ∙ (10)³
V_sphere ≈ 4186.7 cm³

Question 3.
A sphere has a diameter of 3.4 meters. __________________
Answer:
It is given that the diameter of the sphere is 3.4 meters, which means that the radius is 1.7 meters. Therefore, the volume of the sphere is:
V_sphere = \(\frac{4}{3}\)πr³
V_sphere = \(\frac{4}{3}\) ∙ (3.14) ∙ (1.7)³
V_sphere ≈ 20.6 m³

Example 2

Soccer balls come in several different sizes. One soccer ball has a diameter of 22 centimeters. What is the volume of this soccer ball? Round your answer to the nearest tenth. Use 3.14 for π.

Reflect

Question 4.
What is the volume of the soccer ball in terms of π, to the nearest whole number multiple? Explain your answer.
Answer:
V_sphere = \(\frac{4}{3}\)πr³
V_sphere = \(\frac{4}{3}\) ∙ π ∙ (11)³
V_sphere = \(\frac{4}{3}\) ∙ π ∙ 1331
V_sphere = \(\frac{5324}{3}\) ∙ π
V_sphere ≈ 1775 π
The volume of the soccer ball in terms of π, to the nearest whole number multiple, is 1775 πcm³.

Question 5.
Analyze Relationships The diameter of a basketball is about 1.1 times that of a soccer ball. The diameter of a tennis ball is about 0.3 times that of a soccer ball. How do the volumes of these balls compare to that of a soccer ball? Explain.
Answer:
The volume of the soccer ball is
V_soccer = \(\frac{4}{3}\)πr³
Since the diameter of a basketball is about 1.1 times that of a soccer ball, its radius is also 1.1 times that of a soccer ball. Therefore, the volume of the basketball is
V_basketball = \(\frac{4}{3}\) ∙ π ∙ (1.1 r)³
V_basketball = \(\frac{4}{3}\) ∙ π ∙ 1.331 ∙ r³
V_basketball = 1.331 V_soccer
Since the diameter of a tennis ball is about 0.3 times that of a soccer ball, its radius is also 0.3 times that of a soccer ball. Therefore, the volume of the basketball is
V_tennis = \(\frac{4}{3}\) ∙ π ∙ (0.3r)³
V_tennis = \(\frac{4}{3}\) ∙ π ∙ 0.027 ∙ r³
V_tennis = 0.027 V_soccer

Your Turn

Question 6.
Val measures the diameter of a ball as 12 inches. How many cubic inches of air does this ball hold, to the nearest tenth? Use 3.14 for π.
Answer:
Here, the diameter of the ball = 12 inch
so,the radius of the ball = 6 inch
Volume of the sphere = \(\frac{4}{3}\) × π × r³
= \(\frac{4}{3}\) × 3.14 × 6³
= 904.3 in³

Texas Go Math Grade 8 Lesson 9.3 Guided Practice Answer Key

Question 1.
Vocabulary A sphere is a three-dimensional figure with all points ___________ from the center. (Explore Activity)
Answer:
A sphere is a three-dimensional figure with all points the same distance from the center.

Question 2.
Vocabulary The _____________ is the distance from the center of a sphere to a point on the sphere. (Explore Activity)
Answer:
The radius is the distance from the center f the sphere to a point on the sphere.

Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π. (Example 1)

Question 3.

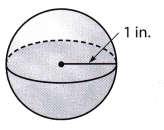
Answer:
Radius r = 1 in
Volume of the sphere = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ 1³
V = 4.1867 in³
V ≈ 4.12 in³

Question 4.

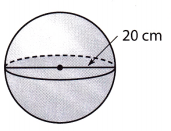
Answer:
Diameter = 20 cm
Radius r = \(\frac{20}{2}\) cm
Radius r = 10 cm
Volume of sphere = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 10³
Volume = 4186.66 cm³
Volume ≈ 4186.7 cm³

Question 5.
A sphere has a radius of 1.5 feet. ___________
Answer:
Radius r = 1.5 ft
Volume of sphere = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 1.5³
Volume = 14.13 ft³
Volume ≈ 14.1 ft³

Question 6.
A sphere has a diameter of 2 yards. ___________
Answer:
Diameter = 2 yards
Radius r = \(\frac{2}{2}\) yards
Radius r = 1 yd
Volume of sphere = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 1³
Volume = 4.1866 yd³
Volume ≈ 4.2 yd³

Question 7.
A baseball has a diameter of 2.9 inches. Find the volume of the baseball. Round your answer to the nearest tenth if necessary. Use 3.14 for π. (Example 2)
Answer:
Diameter of baseball = 2.9 in
Radius r = \(\frac{2.9}{2}\) in
Radius of baseball = 1.45 in
Volume of sphere = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 1.45³
Volume = 12.763 in³
Volume ≈ 12.8 in³

Question 8.
A basketball has a radius of 4.7 inches. What is its volume to the nearest cubic inch? Use 3.14 for π. (Example 2)
Answer:
Radius of basketball r = 4.7 in
Volume of sphere = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 4.7³
Volume = 434.6723 in³
Volume ≈ 434.67 in³

Question 9.
A company is deciding whether to package a ball in a cubic box or a cylindrical box. In either case, the ball will touch the bottom, top, and sides.
(Explore Activity)

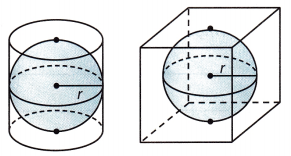
a. What portion of the space inside the cylindrical box is empty? Explain.
Answer:
The volume of the cylinder is
V_cylinder = πr²h
Since the ball touches the bottom, top, and sides, then the height of the cylinder will be equal to 2r.
V_cylinder = π ∙ r² ∙ (2r)
V_cylinder = 2πr³
On the other hand, the voLume of the sphere is
V_sphere = \(\frac{4}{3}\)πr³
The volume of the empty space inside the cylindrical box is found by subtracting the volume of the sphere from the volume of the cylinder:
V_cylinder – V_sphere = 2πr³ – \(\frac{4}{3}\)πr³
= (2 – \(\frac{4}{3}\))πr³
= (\(\frac{6}{3}-\frac{4}{3}\))πr³
= \(\frac{2}{3}\)πr³

b. Find an expression for the volume of the cubic box.
Answer:
The volume of a cube with side a is
V_cube = a³
Since the ball touches the bottom, top, and sides, then the side of the cube will be equal to 2r.
V_cube = (2r)³
V_cube = 8r³

c. About what portion of the space inside the cubic box is empty? Explain.
Answer:
The volume of the empty space inside the cubical box is found by subtracting the volume of the sphere from the volume of the cube:
V_cube – V_sphere = 8r³ – \(\frac{4}{3}\)πr³
= (8 – \(\frac{4}{3}\)π)r³
= (8 – \(\frac{4}{3}\) ∙ 3.14)r³
≈ (8 – 4.2)r³
≈ 3.8r³

Essential Question Check-In

Question 10.
Explain the steps you use to find the volume of a sphere.
Answer:
Step 1: The radius of the sphere is found out
Step 2: The volume of the sphere is \(\frac{4}{3}\)πR³; where R stands for the radius.
Step 3: Put the value of radius in the equation of volume.
Step 4 : Calculate the volume.

Texas Go Math Grade 8 Lesson 9.3 Independent Practice Answer Key

Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 11.
radius of 3.1 meters ____________
Answer:
The voLume of the sphere with a radius of 3.1 meters is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (3.1)³
V ≈ 124.7 m³

Question 12.
diameter of 18 inches __________
Answer:
The diameter of the sphere is 18 inches, which means that its radius is 9 inches. The volume of this sphere is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (9)³
V = 3052.08
V ≈ 3052.1 inches³

Question 13.
r = 6 in. _____________
Answer:
The volume of the sphere with a radius of 6 inches is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (6)³
V = 904.32
V ≈ 904.3 inches³

Question 14.
d = 36 m _____________
Answer:
Diameter d = 36 m
Radius r = \(\frac{36}{2}\) = 18 m
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (18)³
V = 24416.64 m³

Question 15.

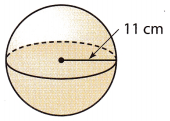
Answer:
The volume of the sphere with a radius of 11 centimeters is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (11)³
V ≈ 5572.5 cm³

Question 16.

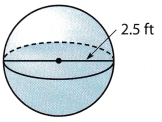
Answer:
The diameter of the sphere is 2.5 feet, which means that its radius is 1.25 feet. The volume of this sphere is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (1.25)³
V ≈ 8.2 feet³

The eggs of birds and other animals come in many different shapes and sizes. Eggs often have a shape that is nearly spherical. When this is true, you can use the formula for a sphere to find their volume.

Question 17.
The green turtle lays eggs that are approximately spherical with an average diameter of 4.5 centimeters. Each turtle lays an average of 113 eggs at one time. Find the total volume of these eggs, to the nearest cubic centimeter.
Answer:
The diameter of an egg (sphere) is 4.5 centimeters, which means that its radius is 2.25 centimeters. The volume of a single egg is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (2.25)³
V ≈ 47.68875 cm³
Therefore, the total volume of 113 eggs is
113 ∙ V = 113 ∙ 47.68875
= 5388.82875
≈ 5389 cm³
The total volume of 113 eggs is approximately 5388.8 cm³

Question 18.
Hummingbirds lay eggs that are nearly spherical and about 1 centimeter in diameter. Find the volume of an egg. Round your answer to the nearest tenth.
Answer:
The diameter of the egg (sphere) is 1 centimeter, which means that its radius is 0.5 centimeters. The volume of a single egg is
V = \(\frac{4}{3}\)πr³
V = \(\frac{4}{3}\) ∙ 3.14 ∙ (0.5)³
V ≈ 0.5233
V ≈ 0.5 cm³

Question 19.
Fossilized spherical eggs of dinosaurs called titanosaurid sauropods were found in Patagonia. These eggs were 15 centimeters in diameter. Find the volume of an egg. Round your answer to the nearest tenth.
Answer:
Diameter of an egg (d) = 15 cm
Radius (r) = \(\frac{15}{2}\) = 7.5 cm
Volume = \(\frac{4}{3}\)πr³
Volume = \(\frac{4}{3}\) × 3.14 × 7.5³
Volume = 1766.25 cm³
Volume ≈ 1766.3 cm³

Question 20.
Persevere in Problem Solving An ostrich egg has about the same volume as a sphere with a diameter of 5 inches. If the eggshell is about \(\frac{1}{12}\) inch thick, find the volume of just the shell, not including the interior of the egg. Round your answer to the nearest tenth.
Answer:
The diameter of the egg, including the eggshell, is
d = 5 + (2 ∙ \(\frac{1}{12}\))
d = 5 + \(\frac{1}{6}\)
d = \(\frac{31}{6}\) inches
Therefore, the radius of the egg, including the eggshell, is
r = \(\frac{d}{2}\)
r = \(\frac{31}{12}\)
r ≈ 2.583 inches
The volume of the egg, including the eggshell, is
V₁ = \(\frac{4}{3}\)πr³
V₁ = \(\frac{4}{3}\) ∙ 3.14 ∙ (2.583)³
V₁ ≈ 72.2 inches³
The diameter of the egg, excluding the eggshell, is 5 inches, which means that its radius ¡s 25 inches The volume of the egg, excluding the eggshell, is
V₂ = \(\frac{4}{3}\)πr³
V₂ = \(\frac{4}{3}\) ∙ 3.14 ∙ (2.5)³
V₂ ≈ 65.4 inches³
To find the volume of just the shell, we subtract the volume of the egg excluding the shell from the volume of the egg including the shell.
V₁ – V₂ = 72.2 – 65.4
V₁ – V₂ = 6.8 inches³
The volume of just the eggshell is approximately 6.8 inches³.

Question 21.
Multistep Write the steps you would use to find a formula for the volume of the figure at right. Then write the formula.

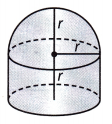
Answer:
Radius of hemisphere = r
Radius of cyLinder = r
Height of cylinder = r
Step 1: Find the formula for volume of hemisphere.
Volume of hemisphere = \(\frac{\frac{4}{3} \pi r^{3}}{2}=\frac{2}{3} \pi r^{3}\)

Step 2: Find the formula for the volume of a cylinder.
Volume of cylinder = πr²h
Height of cylinder is equal to radius, so
Volume of cylinder = πr³

Step 3: Add both the volume expressions:
Total volume = \(\frac{2}{3}\)πr³ + πr³ = \(\frac{5}{3}\)πr³

Question 22.
Critical Thinking Explain what happens to the volume of a sphere if you double the radius.
Answer:
Let radius = r
Volume V₁ = \(\frac{4}{3}\)πr³
Let radius = 2r
Volume V₂ = \(\frac{4}{3}\)π(2r)³
= 8 × \(\frac{4}{3}\)πr³
= 8V₁
= 8 (initial volume)
By doubling the radius of sphere we make the volume 8 times the initial value.

Question 23.
Multistep A cylindrical can of tennis balls holds a stack of three balls so that they touch the can at the top, bottom, and sides. The radius of each ball is 1.25 inches. Find the volume inside the can that is not taken up by the three tennis balls.

Answer:
Radius of a tennis ball = 1.25 in
Diameter of one ball = 2 × 1.25 = 2.5 in
Height of the cylinder = 2.5 × 3 = 7.5 in
Radius of base of cylinder = 125 in
Volume of cylinder (V₁)= πr²h
V₁ = 3.14 × 1.25² × 7.5
V₁ = 36.796875 in³
V₁ ≈ 36.8 in³
Volume of a ball (all three) (V₂) 3 × \(\frac{4}{3}\)πr³
V₂ = 4 × 3.14 × 1.25³
V₂ = 24.53125 in³
V₂ ≈ 24.5 in³
Volume of empty space = Volume of cylinder – Volume of a ball (all three)
= 36.8 – 24.5 = 12.3 in³

H.O.T. Focus on Higher Order Thinking

Question 24.
Critique Reasoning A sphere has a radius of 4 inches, and a cube-shaped box has an edge length of 7.5 inches. J.D. says the box has a greater volume, so the sphere will fit in the box. Is he correct? Explain.
Answer:
Radius of sphere 4 in
Volume of sphere = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)π4³ = 267.9467 in³
Volume of sphere ≈ 267.9 in³
Volume of cube-shaped box = 7.5 ³ = 421.875 in³
Volume of cube-shaped box ≈ 421.9 in³
Volume of cube > Volume of sphere
But the base of the cube has an area of (7.5 × 7.5) = 56.25 in² while the cross-action area of the sphere is:
πr² = 3.14 × 4² = 50.24 in²
The cross-section area of the sphere is less than that of a cube. J.D. is right and the ball (sphere) will fit in the cube.

Question 25.
Critical Thinking Which would hold the most water: a bowl in the shape of a hemisphere with radius r, a cylindrical glass with radius r and height r, or a cone-shaped drinking cup with radius r and height r? Explain.
Answer:
The volume of a sphere with radius r is
V_sphere = \(\frac{4}{3}\)πr³
Therefore, the volume of a hemisphere is
V_hemisphere = \(\frac{V_{\text {sphere }}}{2}\)
V_hemisphere = \(\frac{2}{3}\)πr³
The volume of a cylinder with radius r and height r is
V_cylinder = πr²h
V_cylinder = πr³
The volume of a cone with radius r and height r is
V_cone = \(\frac{1}{3}\)πr²h
V_cone = \(\frac{1}{3}\)πr³
As we can notice
V_cone < V_hemisphere < V_cylinder
Therefore, the cylindrical glass with radius r and height r will hold the most water.

Question 26.
Analyze Relationships Hari has models of a sphere, a cylinder, and a cone. The sphere’s diameter and the cylinder’s height are the same, 2r. The cylinder has radius r. The cone has diameter 2r and height 2r. Compare the volumes of the cone and the sphere to the volume of the cylinder.
Answer:
Diameter of sphere = 2r
Radius r = \(\frac{d}{2}\) = \(\frac{2r}{2}\) = r
Volume of sphere = \(\frac{4}{3}\)πr³
Radius of cylinder = r
Height of cylinder 2r
Volume of cylinder = πr²h = πr²(2r) = 2πr³
Diameter of cone = 2r
Radius of cone r = \(\frac{d}{2}\) = \(\frac{2r}{2}\) = r
Height of cone 2r
Volume of cone = \(\frac{1}{3}\)πr²h = \(\frac{2}{3}\)πr²r = \(\frac{2}{3}\)πr³
Volume of cylinder > Volume of sphere > Volume of cone
2πr³ > \(\frac{4}{3}\)πr³ > \(\frac{2}{3}\)πr³

Question 27.
A spherical helium balloon that is 8 feet in diameter can lift about 17 pounds. What does the diameter of a balloon need to be to lift a person who weighs 136 pounds? Explain.
Answer:
Diameter of heAium balloon = 8 ft
Radius = r = \(\frac{8}{2}\) = 4 ft
Weight it can lift = 17 pounds
Volume of a spherical helium balloon = \(\frac{4}{3}\)πr³ = 4³(\(\frac{4}{3}\)π)

Volume of balloon which can lift 136 pounds is equal to \(\frac{4}{3}\)π8³.
Radius of that balloon = 8 ft
Diameter = 8 × 2 = 16 ft
Diameter of helium balloon = 16 ft