Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Unit 2 Study Guide Review Answer Key.
Texas Go Math Grade 6 Unit 2 Study Guide Review Answer Key
Module 3 Multiplying and Dividing Fractions
Multiply, Write the answer in simplest form.
Question 1.
\(\frac{1}{7} \times \frac{4}{5}\)
Answer:
Solution to this example is given below

Question 2.
\(\frac{5}{6} \times \frac{2}{3}\)
Answer:
Solution to this example is given below

Question 3.
\(\frac{3}{7} \times \frac{14}{15}\)
Answer:
Solution to this example is given below

Question 4.
\(1 \frac{1}{3} \times \frac{5}{8}\)
Answer:
Solution to this example is given below

Question 5.
\(1 \frac{2}{9} \times 1 \frac{1}{2}\)
Answer:
Solution to this example is given below

Question 6.
\(2 \frac{1}{7} \times 3 \frac{2}{3}\)
Answer:
Solution to this example is given below

Divide. Write answer in simplest form.
Question 7.
\(\frac{3}{7} \div \frac{2}{3}\)
Answer:
Solution to this example is given below

Question 8.
\(\frac{1}{8} \div \frac{3}{4}\)
Answer:
Solution to this example is given below

Question 9.
\(1 \frac{1}{5} \div \frac{1}{4}\)
Answer:
Solution to this example is given below

Question 10.
Ron had 20 apples. He used \(\frac{2}{5}\) of the apples to make pies. How many apples did Ron use for pies?
Answer:
Solution to this example is given below

Question 11.
The area of a rectangular garden is 38\(\frac{1}{4}\) square meters. The width of the garden is 4\(\frac{1}{2}\) meters. Find the length of the garden. (Lesson 3.4)
Answer:
Solution to this example is given below

Module 4 Multiplying and Dividing Decimals
Multiply
Question 1.
![]()
Answer:
Solution to this example is given below

Question 2.
![]()
Answer:
Solution to this example is given below

Question 3.
![]()
Answer:
Solution to this example is given below

Divide.
Question 4.
![]()
Answer:
Solution to this example is given below
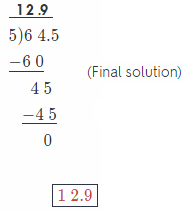
Question 5.
![]()
Answer:
The divisor has one decimal place, so multiply both the dividend and the divisor by 10 so that the divisor is a whole number
0.6 × 10 = 6
25.2 × 10 = 252
Divide
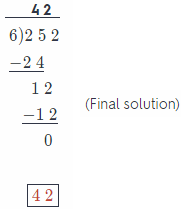
Question 6.
![]()
Answer:
The divisor has one decimal place, so multiply both the dividend and the divisor by 10 so that the divisor is a whole number
2.1 × 10 = 21
36.75 × 10 = 367.5
Divide

Question 7.
Olga worked 37.5 hours last week at the library and earned $12.50 an hour. If she gets a $2.50 per hour raise, how many hours will she have to work to make the same amount of money as she did last week?
Answer:
First, calculate the amount of money that she earned last week:
37.5 × 12.5 = 468.75
She earned $ 468.75.
Now, divide 468.75 by 12.5 + 2.5 to find how many ¡tours site will have to work to make t he same amount of money:
468.75 ÷ (12.5 + 2.5)
Find the stun in the brackets:
468.75 ÷ 15
Use rules for dividing decimals to find the final result:
468.75 ÷ 15 = 31.25
Olga will have to work 31.25 hours to make the same amount of money.
Olga will have to work 3125 hours to make the same amount of money like last week.
Calculate the amount of money she earned last week and divide it by new hourly rate to find the number of hours she will have to work.
Question 8.
A pound of rice crackers costs $2.88. Matthew purchased pound of crackers. How much did he pay for the crackers? (Lesson 4.3)
Answer:
Solution to this example is given below
\(\frac{1}{4}\) = 0.25

For the crackers he pay 0.72 dollars
Module 5 Adding and Subtracting Integers
Add.
Question 1.
– 10 + (- 5)
Answer:
First find absolute values of given integers:
|- 10| = 10 and |- 5| = 5
Then, sum that absolute values
10 + 5 = 15
Final result would be 15 or – 15, depending on sign of given integers (both positive then +, both negative then -).
Given integers are negative so final result is – 15.
Find absolute values, sum them and add minus if both integers were negative.
Question 2.
9 + (- 20)
Answer:
Find absolute values and subtract lesser absolute value from greater:
|9| = 9 and |- 20| = 20
20 – 9 = 11
Final result would be 11 or – 11, depending on signs of given integers.
To find the final result, use the sign of number with greater absolute value:
9 + (- 20) = – 11
The sum is – 11.
Find absolute values, subtract them and add minus if the integer with the greater absolute value was negative.
Question 3.
– 13 + 32
Answer:
Find absolute values and subtract lesser absolute value from greater:
|- 13| = 13 and |32| = 32
32 – 13 = 19
Final result would be 19 or – 19, depending on signs of given integers.
To find the final result use the sign of number with greater absolute value:
– 13 + 32 = – 19
The sum is – 19.
Find absolute values, subtract them and add minus if the integer with the greater absolute value was negative.
Subtract.
Question 4.
– 12 – 5
Answer:
Subtracting 5 is equal to adding its additive inverse – 5 so you can find sum:
– 12 + (- 5)
To calculate sum, find absolute values of given integers:
|- 12| = 12 and |- 5| = 5
Then, sum that absolute values:
12 + 5 = 17
Result would be 17 or – 17. depending on sign of given integers.
Given integers are negative so final result is – 17
Since finding difference – 12 – 5 is the same as finding sum – 12 + (- 5), the difference is – 17.
The difference is – 17
To subtract 5, add its additive inverse – 5 and find sum using rules for adding integers.
Question 5.
25 – (- 4)
Answer:
Subtracting – 4 is equal to adding its additive inverse 4 so you can find sum:
25 + 4
The sum S:
25 + 4 = 29
Since finding difference 25 – (- 4) is the same as finding sum 25 + 4, the difference is 29.
The difference is 29.
To subtract – 4, add its additive inverse 4 and find sum using rules for adding integers.
Question 6.
– 3 – (- 40)
Answer:
Subtracting – 40 is equal to adding its additive inverse 40 so you can find sum:
– 3 + 40
To calculate sum, subtract lesser absolute value from greater:
|40| – |- 3| = 37
Result would be 37 or – 37, depending on signs of given integers.
Use the sign of integer with greater absolute value to find the sum:
– 3 + 40 = 37
Since finding difference – 3 – (- 40) is the same as finding sum – 3 + 40, the difference is 37.
The difference is 37
To subtract – 40, add its additive inverse 40 and find sum using rules for adding integers.
Question 7.
Antoine has $13 in his savings account. He buys some school supplies and ends up with $5 in his account. What was the overall change in Antoine’s account? (Lesson 5.4)
Answer:
The difference:
5 – 13
represents the change in his account
Subtracting 13 is equal to adding its additive inverse – 13 so you can find sum:
5 + (- 13)
To calculate sum, subtract lesser absolute value from greater:
|- 13| – |5| = 8
Result would be 8 or – 8, depending on signs of given integers.
Use the sign of integer with greater absolute value to find the sum:
5 + (- 13) = – 8
Since finding difference
5 – 13
is the same as finding sum
5 + (- 13)
the difference is – 8.
The overall change in his account was – $ 8.
To subtract 13, add its additive inverse – 13 and find sum using rules for adding integers.
Question 8.
Steve finds the value of – 12 + 18. Marion finds the value of – 10 – (- 15). Whose expression has the greater value? (Lesson 5.4)
Answer:
Calculate value of Steve’s expression first
Find absolute values and subtract lesser absolute value from greater:
|18| – |- 12| = 6
Result would be 6 or – 6, depending on signs of given integers.
To find the result use the sign of number with greater absolute value
– 12 + 18 = 6
The value of Steve’s expression is 6.
Then, calculate value of Marion’s expression.
Subtracting – 15 is equal to adding its additive inverse 15 so you can find sum:
– 10 + 15
To calculate sum, subtract lesser absolute value from greater:
|15| – |- 10| = 5
Result would be 5 or – 5, depending on signs of given integers.
Use the sign of integer with greater absolute value to find the sum:
– 10 + 15 = 5
Since finding difference – 10 – (- 5) is the same as finding sum -10 + 5, the difference is 5.
The value of Marion’s expression is 5.
Compare values:
6 > 5
Steve’s expression has greater value.
Use rules for subtracting integers and rules for adding integers to find values and compare them.
Module 6 Multiplying and Dividing Integers
Multiply or divide.
Question 1.
– 9 × (- 5) ____________
Answer:
First, determine if the product will be positive or negative
Since – 9 is negative and – 5 is negative (they have the same sign), the product will, be positive.
Then, multiply absolute values of given integers:
|- 9| = 9 and |- 5| = 5
9 × 5 = 45
The result is 45 or – 45, depending on signs of given integers.
Product is positive so final result is 45.
Result is 45.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus ().
Question 2.
0 × ( – 10) ____________
Answer:
The result is 0.
When you multiply any integer with 0, the result you get is 0.
Question 3.
12 × (- 4) ____________
Answer:
First, determine if the product will be positive or negative
Since 12 is positive and – 4 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|12| = 12 and |- 4| = 4
12 × 4 = 48
The result is 48 or – 48, depending on signs of given integers.
Product is negative so final result is – 48.
Result is – 48
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 4.
– 32 ÷ 8 ____________
Answer:
First, determine if the quotient will be positive or negative
Since – 32 is negative and 8 is positive (they have opposite signs), the quotient will be negative.
Divide given integers:
– 32 ÷ 8 = – 4
Result is – 4.
Find the sign of the quotient (opposite signs of integers then -, the same sign of integers then +) and divide given integers.
Question 5.
– 9 ÷ (- 1) ____________
Answer:
First determine if the quotient will be positive or negative
Since – 9 is negative and – 1 is negative (they have the same sign), the quotient will be positive.
Divide given integers:
(- 9) ÷ (- 1) = 9
Result is 9.
Find the sign of the quotient (opposite signs of integers then -, the same sign of integers then +) and divide given integers.
Question 6.
– 56 ÷ 8 ____________
Answer:
First determine if the quotient will be positive or negative
Since – 56 is negative and 8 is positive (they have the opposite sign), the quotient will be negative.
Divide given integers:
– 56 ÷ 8 = – 7
Result is – 7.
Find the sign of the quotient (opposite signs of integers then -, the same sign of integers then +) and divide given integers.
Simplify.
Question 7.
– 14 ÷ 2 – 3 ____________
Answer:
The expression you want to simplify is:
– 14 ÷ 2 – 3
First, calculate the quotient using rules for dividing integers:
– 7 – 3
Then, find the difference using rules for subtracting integers:
– 7 – 3 = – 10
The expression is equal to – 10
The expression – 14 ÷ 2 – 3 is equal to – 10.
Use rules for dividing integers and rules for subtracting integers to simplify it.
Question 8.
8 + (- 20) × 3 ____________
Answer:
The expression you want to simplify is:
8 + (- 20) × 3
First calculate the product using rules for multiplying integers:
8 + (- 60)
Then, find the sum using rules for adding integers:
8 + (- 60) = – 52
The expression is equal to – 52
The expression 8 + (-20) 3 is equal to – 52.
Use rules for multiplying integers and rules for adding integers to simplify it.
Question 9.
36 ÷ (- 6) – 15 ____________
Answer:
The expression you want to simplify is:
36 ÷ (-6) – 15
First calculate the quotient using rules for dividing integers:
– 6 – 15
Then, find the difference using rules for subtracting integers:
– 6 – 15 = – 21
The expression is equal to – 21
The expression 36 ÷ (- 6) – 15 is equal to – 21.
Use rules for dividing integers and rules for subtracting integers to simplify it
Write an expression to represent the situation. Evaluate the expression and answer the question.
Question 10.
Steve spent $24 on dog grooming supplies. He washed 6 dogs and charged the owners $12 per dog wash. How much money did Steve earn? (Lesson 6.3)
Answer:
Use negative integer to represent the money he spent and positive integer to represent the money he earned for each dog wash
The expression you get is:
– 24 + 6 × 12
First calculate the product using rules for multiplying integers:
– 24 + 72
Then, find the sum using rules for adding integers:
– 24 + 72 = 48
Steve earned $48.
Write an expression that represents his earnings and use rules for multiplying and adding integers to find its value.
Question 11.
Tony and Mario went to the store to buy school supplies. Tony bought 3 packs of pencils for $4 each and a pencil box for $7. Mario bought 4 binders for $6 each and used a coupon for $6 off. Who spent more money? (Lesson 6.3)
Answer:
Calculate how much money spent Tony and how much money spent Mario and compare results to find who spent more money.
The expression that represents Tony’s costs is:
3 × 4 + 7
First calculate the product using rules for multiplying integers:
12 + 7
Then, find the sum using rules for adding integers:
12 + 7 = 19
Tony spent
$ 19.
The expression that represents Mario’s costs is:
4 × 6 – 6
First calculate the product using rules for multiplying integers:
24 – 6
Then, find the difference using rules for subtracting integers:
24 – 6 = 18
Mario spent
$ 18.
Compare their costs
19 > 18
Therefore, Tony spent more money.
Tony spent more money for school supplies.
Use rules for multiplying, adding and subtracting integers to calculate their costs and compare that costs to find who spent more money.
Texas Go Math Grade 6 Unit 2 Performance Task Answer Key
Question 1.
CAREERS IN MATH Chef Chef Alonso is creating a recipe called Spicy Italian Chicken with the following ingredients: \(\frac{3}{4}\) pound chicken, 2\(\frac{1}{2}\) cups tomato sauce, 1 teaspoon oregano, and \(\frac{1}{2}\) teaspoon of his special hot sauce.
a. Chef Alonso wants each serving of the dish to include \(\frac{1}{2}\) pound of chicken. How many \(\frac{1}{2}\) pound servings does this recipe make?
Answer:
The expression that represents number of servings is:
\(\frac{3}{4} \div \frac{1}{2}\)
Use the reciprocal of the divisor to rewrite that expression as multiplication:
\(\frac{3}{4} \times \frac{2}{1}\)
Then, multiply the numerators and multiply the denominators to find the result:
\(\frac{3}{4} \times \frac{2}{1}=\frac{6}{4}\)
Simplify the answer and write ¡tin simplest form:
\(\frac{6 \div 2}{4 \div 2}=\frac{3}{2}\)
Therefore:
\(\frac{3}{4} \div \frac{1}{2}=\frac{3}{2}\), or 1\(\frac{1}{2}\)
That recipe makes 1\(\frac{1}{2}\) servings that each includes \(\frac{1}{2}\) pound of chicken.
b. What is the number Chef Alonso should multiply the amount of chicken by so that the recipe will make 2 full servings, each with \(\frac{1}{2}\) pound of chicken?
Answer:
Calculate the product
2 × \(\frac{1}{2}\)
to find the amount of chicken that is used for 2 servings.
Use rules for multiplying fractions to find that product:
2 × \(\frac{1}{2}\) = \(\frac{2}{2}\)
Simplify the answer and write it in simplest form:
\(\frac{2 \div 2}{2 \div 2}\) = 1
Then, divide the amount of chicken that is used for 2 servings by the amount of chicken from the recipe:
1 ÷ \(\frac{3}{4}\)
Use rules for dividing fractions to find that quotient:
1 × \(\frac{4}{3}\) = \(\frac{4}{3}\)
Therefore:
1 ÷ \(\frac{3}{4}\) = \(\frac{4}{3}\)
Chef should multiply the amount of chicken in recipe by \(\frac{4}{3}\).
c. Use the multiplier you found in part b to find the amount of all the ingredients in the new recipe.
Answer:
Use rules for multiplying fractions to find the solution.
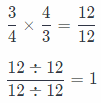
The amount of chicken ¡n new recipe is 1 pound.
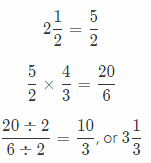
The amount of tomato sauce in new recipe is 3\(\frac{1}{3}\) cups.
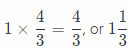
The amount of oregano in new recipe is 1\(\frac{1}{3}\) teaspoons.
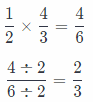
The amount of Chef’s special hot sauce in new recipe is \(\frac{2}{3}\) teaspoon.
d. Chef Alonso only has three measuring spoons: 1 teaspoon, \(\frac{1}{2}\) teaspoon, and \(\frac{1}{4}\) teaspoon. Can he measure the new amounts of oregano and hot sauce exactly? Explain why or why not.
Answer:
New amounts of oregano and hot sauce are 1\(\frac{1}{3}\) teaspoons and \(\frac{2}{3}\) teaspoon.
Convert the amounts of oregano and hot sauce to a decimals You get:
1\(\frac{1}{3}\) = 1,33333…. = 1,\(\dot{3}\)
\(\frac{2}{3}\) = 0,66666… = 0, \(\dot{6}\)
Convert \(\frac{1}{4}\) and \(\frac{1}{2}\) to a decimals:
\(\frac{1}{4}\) = 0,25
\(\frac{1}{2}\) = 0, 5
Numbers that represent the amounts of oregano and hot sauce are not finite and numbers 1, \(\frac{1}{4}\) and \(\frac{1}{2}\) are finite so Chef Alonso cannot measure that amounts exactly with the measuring spoons he has.
Question 2.
Amira is painting a rectangular banner 2\(\frac{1}{4}\) yards wide on a wall in the cafeteria. The banner will have a blue background. Amira has enough blue paint to cover 1\(\frac{1}{2}\) square yards of wall.
a. Find the height of the banner If Amira uses all of the blue paint. Show your work.
Answer:
Write mixed numbers as fractions:
2\(\frac{1}{4}\) = \(\frac{9}{4}\)
1\(\frac{1}{2}\) = \(\frac{3}{2}\)
Since the formula for calculating area of rectangle is:
area = width × height,
the quotient
area ÷ width
represents the height of rectangle.
Therefore, quotient
\(\frac{3}{2} \div \frac{9}{4}\)
represents the height of the banner.
Use the reciprocal of the divisor to rewrite that exDression as multiplication:
\(\frac{3}{2} \times \frac{4}{9}\)
Then, multiply the numerators and multiply the denominators to find the result:
\(\frac{3}{2} \times \frac{4}{9}=\frac{12}{18}\)
Simplify the answer and write it in simplest form:
\(\frac{12 \div 6}{18 \div 6}=\frac{2}{3}\)
The height of the banner is \(\frac{2}{3}\) yards.
b. The school colors are blue and yellow, so Amira wants to add yellow rectangles on the left and right sides of the blue rectangle. The yellow rectangles will each be \(\frac{3}{4}\) yard wide and the same height as the blue rectangle. What will be the total area of the two yellow rectangles? Explain how you found your answer.
Answer:
The height of the yellow rectangles will be \(\frac{2}{3}\) yards.
Find the area of one yellow rectangle and multiply it by 2 to find the total area.
The expression you get is:
\(\left(\frac{3}{4} \times \frac{2}{3}\right)\) × 2
First multiply the numerators and multiply the denominators to find the product in the brackets:
\(\frac{6}{12}\) × 2
Then, use rules for multiplying fractions to find the final result:
\(\frac{6}{12}\) × 2 = \(\frac{12}{12}\)
Simplify the answer and write it in simplest form:
\(\frac{12 \div 12}{12 \div 12}\) = 1
The total area of two yellow rectangles will be 1 square yard.
c. What are the dimensions of the banner plus yellow rectangles? What is the total area? Show your work.
Answer:
Width of blue banner is \(\frac{9}{4}\) yards and width of each yellow rectangle is \(\frac{3}{4}\) yard so total width is:
\(\frac{9}{4}\) + 2 × \(\frac{3}{4}\)
Use rules for multiplying fractions and rules for adding fractions to find the result:
\(\frac{9}{4}+\frac{6}{4}\)
\(\frac{9}{4}+\frac{6}{4}=\frac{15}{4}\)
Total width is \(\frac{15}{4}\) yards.
Height of blue banner is the same as height of yellow rectangles so
total height is \(\frac{2}{3}\) yard
Multiply total width and total height using rules for multiplying fractions to find the total area:
\(\frac{15}{4} \times \frac{2}{3}=\frac{30}{12}\)
Simplify the answer and write it in simplest form:
\(\frac{30 \div 6}{12 \div 6}=\frac{5}{2}\) or 2\(\frac{1}{2}\)
The total area is 2\(\frac{1}{2}\) square yards.
Texas Go Math Grade 6 Unit 1 Texas Test Prep Answer Key
Selected Response
Question 1.
Which of the following statements is correct?
(A) The product of \(\frac{5}{6}\) and \(\frac{9}{10}\) is greater than.
(B) The product of 1\(\frac{3}{4}\) and \(\frac{3}{4}\) is less than 1\(\frac{1}{5}\).
(C) The product of \(\frac{6}{7}\) and \(\frac{5}{6}\) is greater than \(\frac{5}{6}\).
(D) The product of 1\(\frac{3}{4}\) and \(\frac{2}{5}\) is less than \(\frac{2}{5}\).
Answer:
(B) The product of 1\(\frac{3}{4}\) and \(\frac{3}{4}\) is less than 1\(\frac{1}{5}\).
Explaination:
(A) Calculate the product:
\(\frac{5}{6} \times \frac{9}{10}\)
Multiply the numerators and multiply the denominators to find the result:
\(\frac{5}{6} \times \frac{9}{10}=\frac{45}{60}\)
Write in form in which it has the same denominator as previous product, \(\frac{45}{60}\):
\(\frac{9 \times 6}{10 \times 6}=\frac{54}{60}\)
Compare the product with that fraction:
\(\frac{45}{60}<\frac{54}{60}\)
The product is less than \(\frac{9}{10}\).
Therefore, statement A) is incorrect.
(B) Write mixed number as fraction:
1 \(\frac{1}{5}\) = \(\frac{6}{5}\)
Calculate the product:
\(\frac{6}{5} \times \frac{6}{7}\)
Multiply the numerators and multiply the denominators to find the result:
\(\frac{6}{5} \times \frac{6}{7}=\frac{36}{35}\)
Write \(\frac{6}{5}\) in form in which it has the same denominator as previous product, \(\frac{36}{35}\):
\(\frac{6 \times 7}{5 \times 7}=\frac{42}{35}\)
Compare the product with that fraction:
\(\frac{36}{35}<\frac{42}{35}\)
The product is less than 1\(\frac{1}{5}\) so the correct answer is B.
Use same rules to check statements C and D:
(C)
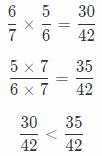
The product is less than \(\frac{5}{6}\).
(D)
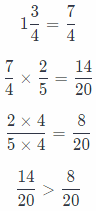
The product is greater than \(\frac{2}{5}\).
Therefore, statements (C) and (D) are incorrect.
Question 2.
Which of these is the same as \(\frac{8}{9} \div \frac{2}{3}\)
(A) \(\frac{8}{9} \div \frac{3}{2}\)
(B) \(\frac{2}{3} \div \frac{8}{9}\)
(C) \(\frac{8}{9} \times \frac{2}{3}\)
(D) \(\frac{8}{9} \times \frac{3}{2}\)
Answer:
(D) \(\frac{8}{9} \times \frac{3}{2}\)
Explaination:
Given expression:
\(\frac{8}{9} \div \frac{2}{3}\)
Convert the divide sign to a multiply sign by taking the reciprocal of the fraction after the divide sign, therefore:
= \(\frac{8}{9} \times \frac{3}{2}\)
Question 3.
A rectangular tabletop has a length of 4\(\frac{3}{4}\) feet and an area of 11\(\frac{7}{8}\) square feet. What is the width of the tabletop?
(A) 1\(\frac{1}{16}\) feet
(B) 2\(\frac{1}{2}\) feet
(C) 4\(\frac{1}{4}\) feet
(D) 8\(\frac{1}{2}\) feet
Answer:
(B) 2\(\frac{1}{2}\) feet
Exaplaination:
Write mixed numbers as fractions:
4\(\frac{3}{4}\) = \(\frac{19}{4}\)
11\(\frac{7}{8}\) = \(\frac{95}{8}\)
Since the formula for calculating the area of rectangle is:
area = length × width,
the quotient
area ÷ length
represents the width of rectangle.
Therefore, the quotient
\(\frac{95}{8} \div \frac{19}{4}\)
represents me width of the tabletop.
Use the reciprocal of the divisor to rewrite that expression as multiplication:
\(\frac{95}{8} \times \frac{4}{19}\)
Then, multiply the numerators and multiply the denominators to find the result:
\(\frac{95}{8} \times \frac{4}{19}=\frac{380}{152}\)
Simplify the answer and write it in simplest form:
\(\frac{380 \div 76}{152 \div 76}=\frac{5}{2}\), or 2\(\frac{1}{2}\)
The width of the rectangular tabletop is 2\(\frac{1}{2}\) feet.
Question 4.
Dorothy types 120 words per minute. How many words does Dorothy type in 1.75 minutes?
(A) 150 words
(B) 180 words
(C) 200 words
(D) 210 words
Answer:
(D) 210 words
Explaination:
Solution to this example is given below

Question 5.
What is the opposite of 17?
(A) – 17
(B) –\(\frac{1}{17}\)
(C) \(\frac{1}{17}\)
(D) 17
Answer:
(A) – 17
Explaination:
Solution to this example is given below
17 × (- 1)
– 17 × 1 (Remove parentheses)
– 17 (Multiply the numbers)
Question 6.
Each paper clip is of an inch long and costs $0.03. Exactly enough paper clips are laid end to end to have a total length of 56 inches. What is the total cost of these paper clips?
(A) $0.49
(B) $0.64
(C) $1.47
(D) $1.92
Answer:
(D) $1.92
Explaination:
The number of paper clips required to make a length of 56 inches is evaluated as \(\frac{56}{\frac{7}{8}}=\frac{56 \times 8}{7}\) = 64.
Total cost to buy these 64 clips is 64 × $0.03 = $1.92.
Question 7.
Which expression simplifies to 5?
(A) \(\frac{27}{3}\) – 14
(B) \(\frac{27}{3}\) + 14
(C) \(\frac{-27}{3}\) – 4
(D) \(\frac{-27}{3}\) + 14
Answer:
(D) \(\frac{-27}{3}\) + 14
Explaination:
(A) \(\frac{27}{3}\) – 14
Calculate the quotient using rules for dividing integers:
9 – 14
Find the difference using rules for subtracting integers:
9 – 14 = – 5
The expression is equal to – 5 so it is not the answer.
(B) \(\frac{27}{3}\) + 4
Calculate the quotient using rules for dividing integers:
9 + 4
Find the difference using rules for subtracting integers:
9 + 4 = 13
The expression is equal to 13 so it is not the answer.
(C) \(\frac{-27}{3}\) – 4
Calculate the quotient using rules for dividing integers:
– 9 – 4
Find the difference using rules for subtracting integers:
– 9 – 4 = – 13
The expression is equal to – 13 so it is not the answer.
(D) \(\frac{-27}{3}\) + 14
Calculate the quotient using rules for dividing integers:
– 9 + 14
Find the difference using rules for subtracting integers:
– 9 + 14 = 5
The expression is equal to 5 so the correct answer is D.
Question 8.
What is the absolute value of – 36?
(A) -36
(B) 0
(C) 6
(D) 36
Answer:
(D) 36
Exaplaination:
Solution to this example is given below
|- 36| = 36 (This option is correct answer)
Apply absolute rule: |- a| = a
Question 9.
Which number can you add to 13 to get a sum of 0?
(A) – 26
(B) – 13
(C) 0
(D) 13
Answer:
(B) – 13
Explaination:
Add each number to 13 using rules for adding integers to find the result of 0.
(A) 13 + (- 26)
Find absolute values and subtract lesser absolute value from greater:
|- 26| – |13| = 13
Final result would be 13 or – 13, depending on signs of given integers.
Use the sign of the number with the greater absolute value to find the result:
13 + (- 26) = – 13
– 13 is not equal to 0 so A) is not the answer
(B) 13 + (- 13)
Find absolute values and subtract lesser absolute value from greater:
|- 13| – |13| = 0
Final result is 0 so the correct answer is B.
Question 10.
Joseph owes his older brother $15, so he has a balance of – $15 with his brother. Joseph borrows some more money from his brother, bringing his balance to 5 times the previous amount. What is Joseph’s new balance with his brother?
(A) – $ 90
(B) – $ 75
(C) – $ 10
(D) $ 60
Answer:
(B) – $ 75
Multiply Josephs balance of – $15 by 5 to find bis new balance.
The expression you get is:
5(- 15)
First, determine if the product will be positive or negative.
Since 5 is positive and – 15 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|5| = 5 and |- 15| = 15
5 × 15 = 75
The result is 75 or – 75. depending on signs of given integers.
Product is negative so final result is – 75.
he answer is B. His new balance with his brother is – $ 75.
Question 11.
Which expression simplifies to a positive answer?
(A) a negative number divided by a positive number
(B) a positive number divided by a negative number
(C) a negative number multiplied by a negative number
(D) a positive number multiplied by a negative number
Answer:
(C) a negative number multiplied by a negative number
Explaination:
The product of two integers with the same sign is positive so the correct answer is C.
The quotient of two integers with different signs is negative as well as the product of two integers with different signs so results of expressions A), B) and D) are negative.
Question 12.
Which expression has the least value?
(A) (- 9) ÷ 3 – 2
(B) (- 24) ÷ 6 + 2
(C) 36 ÷ (- 4) + 7
(D) (- 32) ÷ 8 – 4
Answer:
(D) (- 32) ÷ 8 – 4
Exaplaination:
Find value of each expression and compare results you get
(A) (- 9) ÷ 3 – 2
Calculate the quotient using rules for dividing integers:
– 3 – 2
Find the difference using rules for subtracting integers:
– 3 – 2 = – 5
(- 9) ÷ 3 – 2 = – 5
(B) (- 24) ÷ 6 + 2
Calculate the quotient using rules for dividing integers:
– 4 + 2
Find the sum using rules for adding integers:
– 4 + 2 = – 2
(- 24) ÷ 6 + 2 = – 2
(C) 36 ÷ (-4) + 7
Calculate the quotient using rules for dividing integers:
– 9 + 7
Find the sum using rules for adding integers:
– 9 + 7 = – 2
36 ÷ (- 4) + 7 = – 2
(D) (- 32) ÷ 8 – 4
Calculate the quotient using rules for dividing integers:
– 4 – 4
Find the difference using rules for subtracting integers:
– 4 – 4 = -8
(- 32) ÷ 8 – 4 = – 8
Compare results:
– 8 < – 5 < – 2
The expression D) has the least value.
Gridded Response
Hot Tip! Make sure that your answer makes sense before marking it as your response. Reread the question and determine whether your answer is reasonable.
Question 13.
A fish is 73 feet below sea level. It then swims 14 feet toward the surface. How many feet below sea level is the fish now?
Answer:
Use negative integer to represent where fish was at the beginning and positive integer to represent the distance it moves toward the surface.
The expression you get is:
– 73 + 14
Find absolute values and subtract lesser absolute value from greater:
|- 73| – |14| = 59
Final result would be 59 or – 59, depending on signs of given integers.
Use sign of number with greater absolute value to find the final result:
– 73 + 14 = – 59
The fish is 59 feet below the surface.
Use rules for adding integers to find how many feet below sea level the fish is now.
Question 14.
A box contained 162 matches. A bigger box contained 1\(\frac{4}{9}\) times as many matches. How many matches did the bigger box contain?
Answer:
Multiply 162 by 1\(\frac{4}{9}\) to find how many matches the bigger box contained.
The expression you get is:
162 × 1\(\frac{4}{9}\)
First, write 1\(\frac{4}{9}\) as a fraction:
1\(\frac{4}{9}\) = \(\frac{13}{9}\)
Then, multiply the numerators and multiply the denominators to find the result:
\(\frac{162}{1} \times \frac{13}{9}=\frac{2106}{9}\)
Simplify the answer and write it in simplest form:
\(\frac{2106 \div 9}{9 \div 9}\) = 234
The bigger box contained 234 matches.
Use rules for multiplying fractions to find the result.
Question 15.
Colby and his 3 friends buy lunch. The total is $30.60. If they share the cost equally, how much, in dollars, should each person pay?
Answer:
Divide 30.60 by 4 to find how much money each person should pay.
The expression you get is:
30.60 ÷ 4
Use rules for dividing decimals to find the final result:
30.60 ÷ 4 = 7.65
Each person should pay $7.65.
Use rules for dividing decimals to calculate how much money each person should pay.