Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 12.3 Answer Key Properties of Rotations.
Texas Go Math Grade 8 Lesson 12.3 Answer Key Properties of Rotations
Texas Go Math Grade 8 Lesson 12.3 Explore Activity Answer Key
Explore Activity 1
Exploring Rotations
A rotation is a transformation that turns a figure around a given point called the center of rotation. The image has the same size and shape as the preimage.

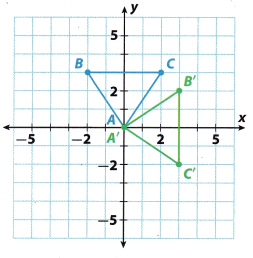
The triangle shown on the grid is the preimage. You will use the origin as the center of rotation.
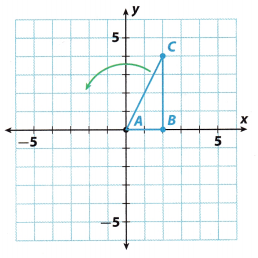
A. Trace triangle ABC onto a piece of paper. Cut out your traced triangle.
B. Rotate your triangle 90° counterclockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.
C. Sketch the image of the rotation. Label the images of points A, B, and C as A’, B’, and C’.
D. Describe the motion modeled by the rotation.
Rotate ________________ degrees ____________________ about the origin.
E. Check that the motion you described in, D is the same motion that maps point A onto A’, point B onto B’, and point C onto C’.
Reflect
Question 1.
Communicate Mathematical Ideas How are the size and the orientation of the triangle affected by the rotation?
Answer:
A rotation is a transformation that turns a figure around a given point called the center of rotation.
The image has the same size and shape as the preimage, but different orientation.
For example, the side \(\overline{\mathrm{BC}}\) was vertical and on the image, it will be horizontal.
Question 2.
Rotate triangle ABC 90° clockwise about the origin. Sketch the result on the coordinate grid above. Label the image vertices A”, B”, and C”.
Answer:
After a 900 cLockwise rotation, the vertices of the triangle wilL be:
A(0, 0) → A”(0, 0)
B(2, 0) → B”(0, -2)
C(2, 4) → C”(4, -2)
Explore Activity 2
Properties of Rotations
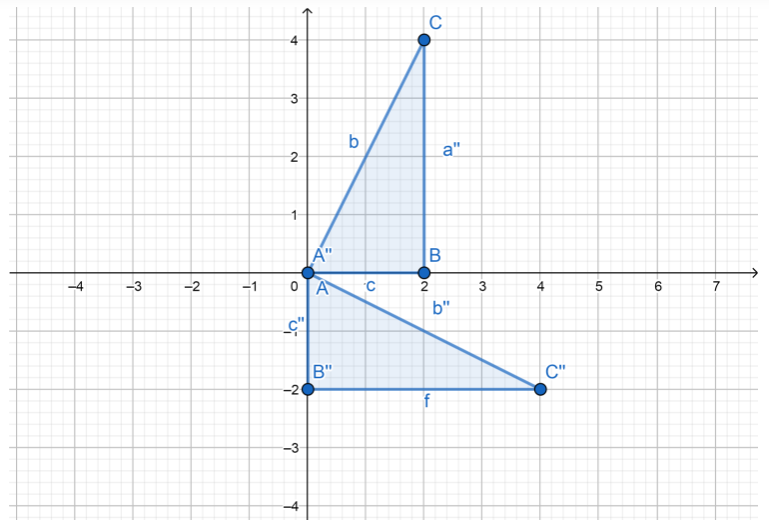
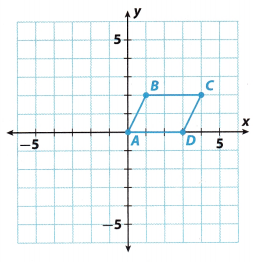
Use trapezoid TRAP to investigate the properties of rotations.
A. Trace the trapezoid onto a piece of paper. Include the portion of the x- and y-axes bordering the third quadrant. Cut out your tracing.
B. Place your trapezoid and axes on top of those in the figure. Then use the axes to help rotate your trapezoid 180° counterclockwise about the origin. Sketch the image of the rotation of your trapezoid in this new location. Label the vertices of the image T’, R’ A’, and P’.
C. Use a ruler to measure the sides of trapezoid TRAP in centimeters.
TR = ____________ RA = ____________ AP = ____________ TP = ____________
D. Use a ruler to measure the sides of trapezoid T’R’A’P’ in centimeters.
T’R’ = ____________ R’A’ = ____________ A’P’ = ____________ T’P’ = ____________
E. What do you notice about the lengths of corresponding sides of the two figures?
F. Use a protractor to measure the angles of trapezoid TRAP.
m∠J = ____________ m∠R = ____________ m∠A = ____________ m∠P = ____________
G. Use a protractor to measure the angles of trapezoid T’R’A’P’.
m∠T’ = ____________ m∠R’ = ____________ m∠A’ = ____________ m∠P’ = ____________
H. What do you notice about the measures of corresponding angles of the two figures?
I. Which sides of trapezoid TRAP are parallel?
Which sides of trapezoid T’R’A’P’ are parallel?
What do you notice?
Reflect
Question 3.
Make a Conjecture Use your results from E, H, and I to make a conjecture about rotations.
Answer:
The image of a figure and its preimage have the same length of sides and the same interior angles, that means that two figures are congruent.
Question 4.
Place your tracing back in its original position. Then perform a 180° clockwise rotation about the origin. Compare the result.
Answer:
The image will be the same after a 180° clockwise rotation and after a 180° counterclockwise rotation.
Question 5.
Is the image congruent to the preimage? How do you know?
Answer:
The image of a figure and its preimage have the same size and shape, so this means that two figures are congruent.
Your Turn
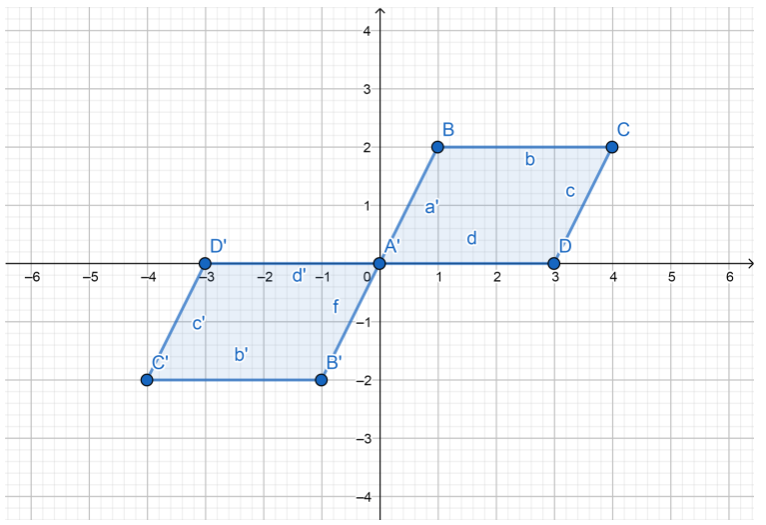
Graph the image of quadrilateral ABCD after each rotation.
Question 6.
180°
Answer:
Step 1: Rotate the figure clockwise from y-axis to the x-axis. Point A will still be at (0, 0).
Plot point; B'(- 1, 2).
Plot point; C'(- 4, 2).
Plot point; D'(- 3, 0)
Step 2: Connect A’, B’, C’ and D’ to form the image quadrilateraL A’B’C’D’.
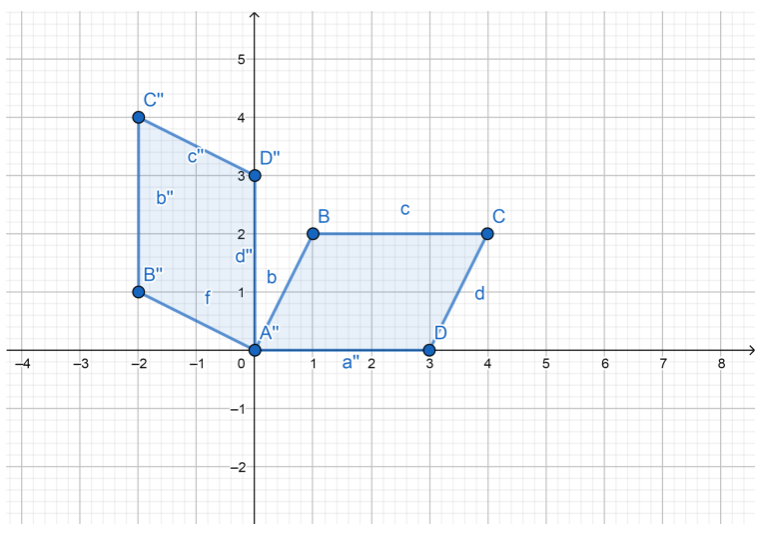
Question 7.
270° clockwise
Answer:
Step 1: Rotate the figure clockwise from y-axis to the x-axis. Point A will still be at (0,0).
Plot point B”(-2, 1).
Plot point C”(-2, 4).
Plot point D”(0, 3).
Step 2: Connect A”, B”, C” and D” to form the image quadrilateral A”B”C”D’.
Question 8.
Find the coordinates of Point C after a 90° counterclockwise rotation followed by a 180° rotation.
Answer:
Coordinates of point C after a 90° counterclockwise rotation followed by a 180° rotation are (2, -4).
Texas Go Math Grade 8 Lesson 12.3 Guided Practice Answer Key
Question 1.
Vocabulary A rotation is a transformation that turns a figure around a given _____________________ called the center of rotation.
Answer:
A rotation is a transformation that turns a figure around a given point called the center of rotation.
Siobhan rotates a right triangle 90° counterclockwise about the origin.
Question 2.
How does the orientation of the image of the triangle compare with the orientation of the preimage? (Explore Activity 1)
Answer:
The image has the same size and shape as the preimage. but different orientation.
Question 3.
Is the image of the triangle congruent to the preimage? (Explore Activity 2)
Answer:
The image of the figure and its preimage have the same size and shape, so this means that two figures are congruent.
Draw the image of the figure after the given rotation about the origin. (Example 1)
Question 4.
90° counterclockwise
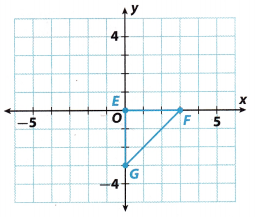
Answer:
Step 1: Rotate the figure counterclockwise from the x-axis to the y-axis. Point E will still be (0, 0)
Plot point F'(0, 3).
Plot point G'(3, 0).
Step 2: Connect E’, F’ and G’ to form the image triangle E’F’G’.
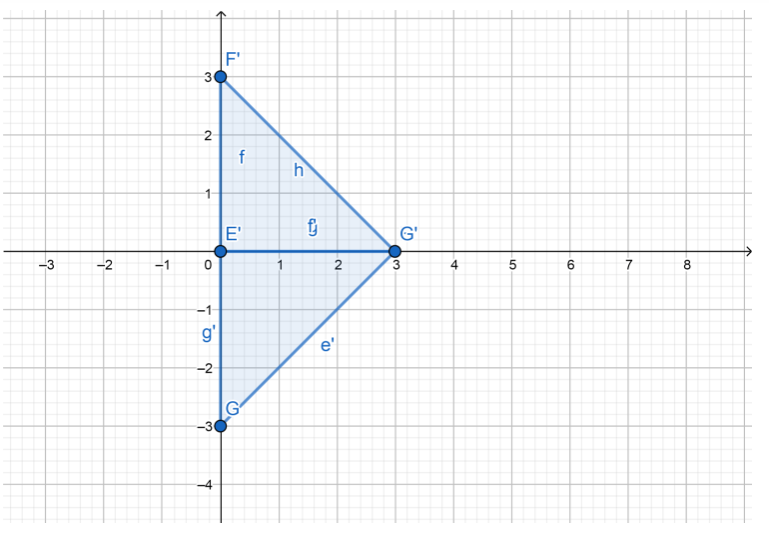
Question 5.
180°
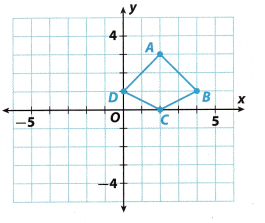
Answer:
Step 1: Points will be A'(-2, -3).
B'(-4, -1)
C'(-2, 0)
D'(0, -1)
Step 2: Connect A’, B’, C’ and D’ to form the image quadrilateral A’B’C’D’.
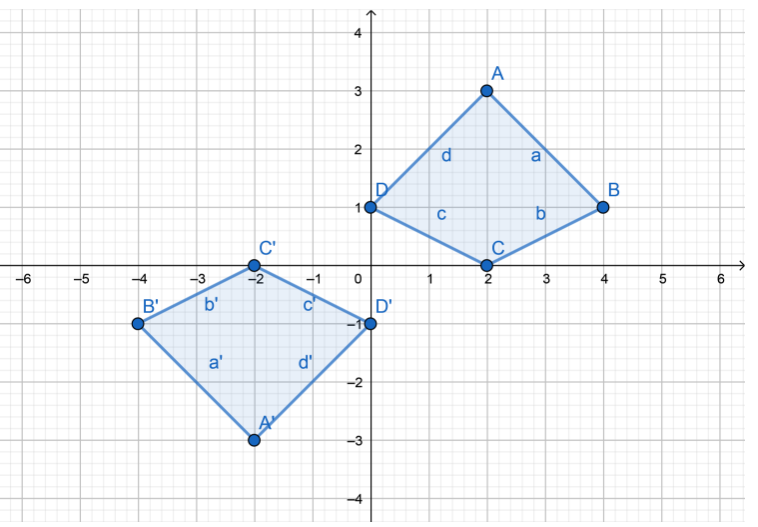
Essential Question Check-In
Question 6.
What are the properties of rotations?
Answer:
The image and its preimage have the same size and shape, but different orientation.
Texas Go Math Grade 8 Lesson 12.3 Independent Practice Answer Key
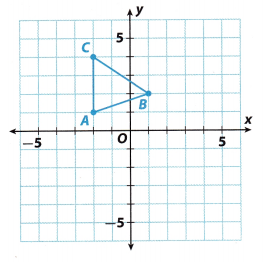
Question 7.
The figure shows triangle ABC and a rotation of the triangle about the origin.
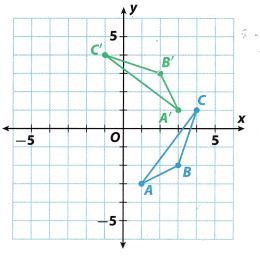
a. How would you describe the rotation?
Answer:
The triangle was rotated 90° counterclockwise about the origin.
b. What are the coordinates of the image?
Answer:
The coordinates of the image are:
A'(3, 1), B'(2, 3) and C'(-1, 4).
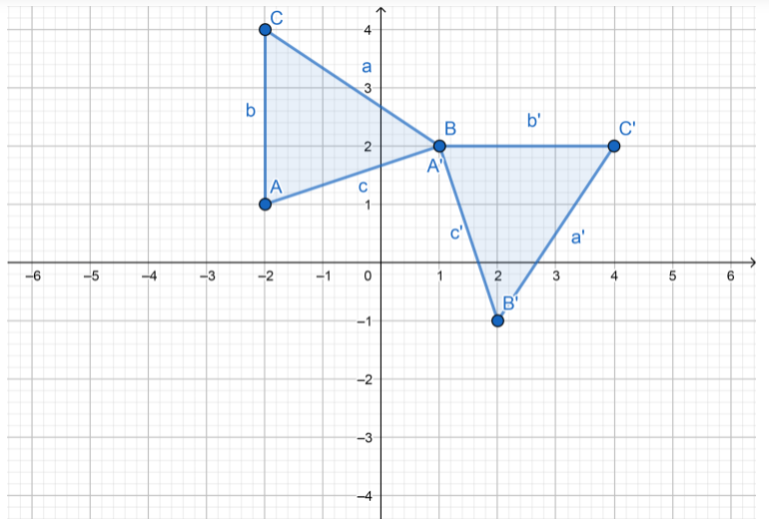
Question 8.
The graph shows a figure and its image after a transformation.
a. How would you describe this as a rotation?
Answer:
The figure was rotated 180° about the origin.
b. Can you describe this as a transformation other than a rotation? Explain.
Answer:
Yes, this transformation also can be a reflection across the y-axis.
Question 9.
What type of rotation will preserve the orientation of the H-shaped figure in the grid?
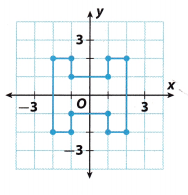
Answer:
A 180° rotation about the origin will preserve the orientation of the H-shaped figure in the grid.
Question 10.
A point with coordinates (-2, -3) is rotated 90° clockwise about the origin. What are the coordinates of its image?
Answer:
The coordinates of its image are (-3, 2).
Complete the table with rotations of 180° or less. Include the direction of rotation for rotations of less than 180°.
Question 11.

Answer:
If the shape is in quadrant I and the image is in quadrant IV, the rotation is 90° clockwise.
Question 12.

Answer:
If the shape is in quadrant III and the image in quadrant I, the rotation is 180°.
Question 13.

Answer:
If the shape is in IV quadrant and the image is in III quadrant, the rotation is 90° clockwise.
Draw the image of the figure after the given rotation about the origin.
Question 14.
180°
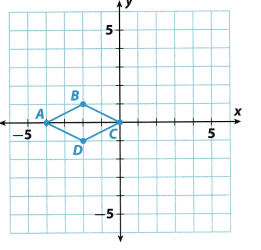
Answer:
Step 1: After the 180° rotation about the origin, points will be;
A'(4, 0).
B'(2, -1)
C'(0, 0)
D'(2, 1)
Step 2: Connect A’, B’, C’ and D’ to form the image quadrilateral A’B’C’D’.
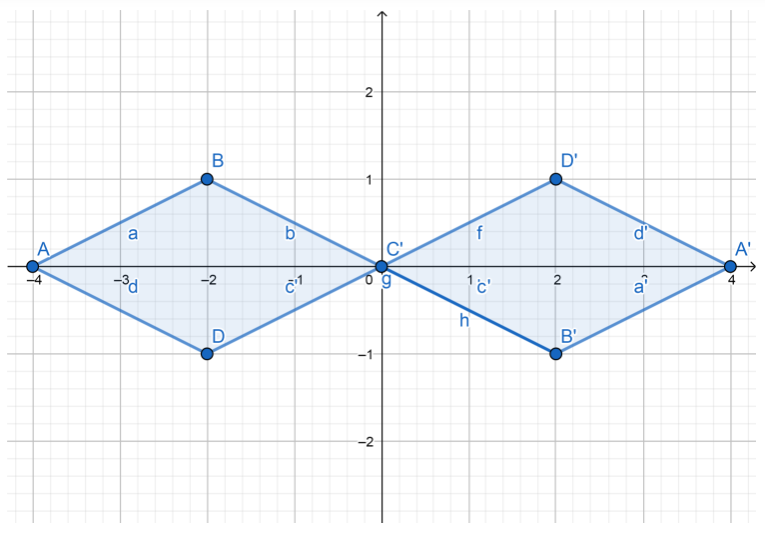
Question 15.
270° counterclockwise
Answer:
Step 1: After the 270° counterclockwise rotation, the points will be:
A'(1, 2)
B'(2, -1)
C'(4, 2)
Step 2: Connect points A’, B’ and C’ to form image triangle A’B’C’.
Question 16.
Is there a rotation for which the orientation of the image is always the same as that of the preimage? If so, what?
Answer:
Yes, there is 360° rotation With that rotation the orientation of the image is always the same as that of the preimage.
H.O.T. Focus on Higher Order Thinking
Question 17.
Problem Solving Lucas is playing a game where he has to rotate a figure for it to fit in an open space. Every time he clicks a button, the figure rotates 90 degrees clockwise. How many times does he need to click the button so that each figure returns to its original orientation?
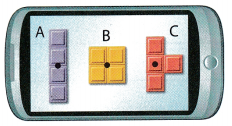
Figure A _______________
Figure B _______________
Figure C _______________
Answer:
Figure A – 2 times to return to original orientation
Figure B – 1 times to return to original orientation
Figure B – 4 times to return to original orientation
Question 18.
Make a Conjecture Triangle ABC is reflected across the y-axis to form the image A’B’C’. Triangle A’B’C’ is then reflected across the x-axis to form the image A”B”C”. What type of rotation can be used to describe the relationship between triangle A”B”C” and triangle ABC?
Answer:
Triangle A’B’C’ is a 90° rotation of triangle ABC
Triangle A”B”C” is a 90° rotation of triangle A’B’C’.
Therefore,
Triangle A”B”C” is a 180° rotation of triangle ABC
Question 19.
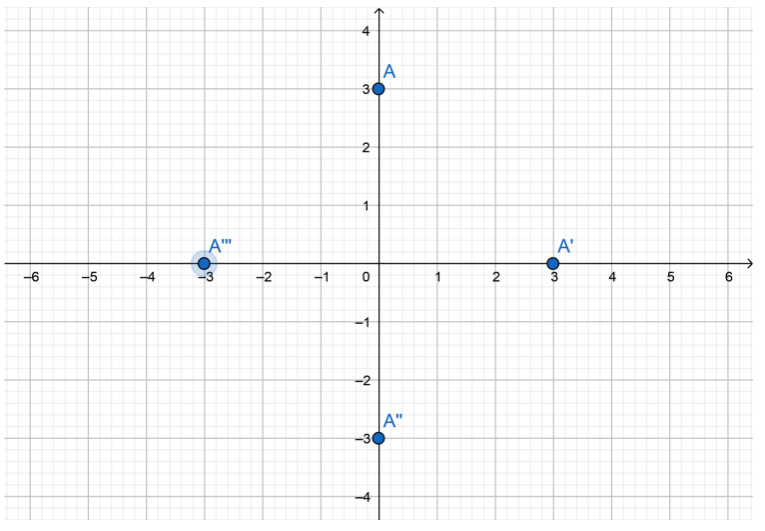
Communicate Mathematical Ideas Point A is on the y-axis. Describe all possible locations of image A’ for rotations of 90°, 180°, and 270°. Include the origin as a possible location for A.
Answer:
If point A is on the y-axis, for 90° clockwise rotation and for the 90° counterclockwise rotation, the image will be on the x-axis.
If point A is on the y-axis, for 270° clockwise rotation and for the 270° counterclockwise rotation, the image will be on the x-axis.
If point A is on the y-axis, for 180° rotation the image will still be on the y-axis.
If point A is at the origin, A’ is at the origin for any rotation about the origin.
For example, for point A(0, 3), possible locations are:
A'(3, 0) after a 90° clockwise rotation;
A”(0, -3) after a 180° rotation;
A”(-3, 0) after a 270° clockwise rotation.