Texas Go Math Grade 6 Module 16 Quiz Answer Key

Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Module 16 Quiz Answer Key.

Texas Go Math Grade 6 Module 16 Quiz Answer Key

Texas Go Math Grade 6 Module 16 Ready to Go On? Answer Key

16.1 Area of Quadrilaterals

Question 1.
Find the area of the figure.

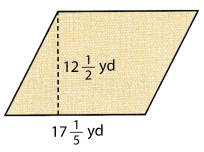
Answer:
Data:
b = 17\(\frac{1}{5}\) = 17.2
h = 12\(\frac{1}{2}\) = 12.5
Write equation of area of a parallelogram:
Area = b × h
Substitute values:
Area = 17.2 × 12.5
Evaluate:
Area = 215
Area of the given parallelogram is 215 square yards.

16.2 Area of Triangles

Question 2.
Find the area of the triangle.

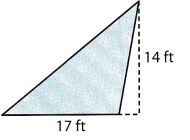
Answer:
Find the area of the triangle.
b = 17 feet; h = 14 feet
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (17 feet) (14 feet) Substitute
= 119 square feet Multiply
= 119 ft²

16.3 Solving Area Equations

Question 3.
A triangular pane of glass has a height of 30 inches and an area of 270 square inches. What is the length of the base of the pane?
Answer:
What is the base of the triangular?
A = \(\frac{1}{2}\) bh Write the formula
270 = \(\frac{1}{2}\) b (30) Use the formula to write an equation
270 = 15b Multiply \(\frac{1}{2}\) and 30
\(\frac{270}{15}=\frac{15 b}{15}\) Divide both sides of the equation by 15
18 = b
The base of the triangular is 18 inches long.

Question 4.
A tabletop in the shape of a trapezoid has an area of 6,550 square centimeters. Its longer base measures 115 centimeters, and the shorter base is 85 centimeters. What is the height?
Answer:
What is the height of the trapezoid?
A = \(\frac{1}{2}\) h(b₁ + b2) Write the formula
6550 = \(\frac{1}{2}\) h(85 + 115) Use the formula to write an equation
6550 = \(\frac{1}{2}\) h(200) Add inside parentheses
6550 = 100h Multiply \(\frac{1}{2}\) and 200
\(\frac{6550}{100}=\frac{100 h}{100}\) Divide both sides of the equation by 100
65.5 = h
The height of the trapezoid is 65.5 centimeters

16.4 Solving Volume Equations

Question 5.
A rectangular shoebox has a volume of 728 cubic inches. The base of the shoebox measures 8 inches by 6.5 inches. How long is the shoebox?
Answer:
Determine the volume of the box.
V = lwh formula for the volume of a box
728 = l ∙ 8 ∙ 6 ∙ 5 substitute for the given values
728 = 52l simplify
\(\frac{728}{52}=\frac{52 l}{52}\) divide both sides by 52
14 inches = l Length of the shoebox
The shoebox is 14 inches long.

Essential Question

Question 6.
How can you use equations to solve problems involving area and volume?
Answer:
Equations will help in solving problems involving area and volume. Identify the dimensions of the figure then substitute for the given values in the equation.
Area of a Rectangle = l × W
Area of a Parallelogram = b × h
Area of aTriangle = \(\frac{1}{2}\)bh
Area of a Trapezoid = \(\frac{1}{2}\)h (b₁ + b₂)
Area of a Rhombus = \(\frac{1}{2}\)d₁d₂
Volume of a Rectangular Prism = l × w × h
Identify the dimensions then substitute for the given equations.

Texas Go Math Grade 6 Module 16 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
What is the area of the rhombus shown below?

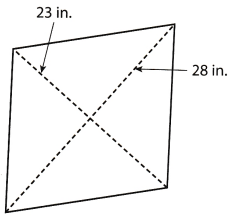
(A) 161 in²
(B) 322 in²
(C) 644 in²
(D) 966 in²
Answer:
(B) 322 in²

Explanation:
Determine the area of the rhombus.
A = \(\frac{1}{2}\) ∙ 23 ∙ 28 substitute for the given values
A = \(\frac{644}{2}\) simplify
A = 322 in² area of the rhombus
The area of the rhombus is 322 in².

Question 2.
What is the area of the triangle shown below?

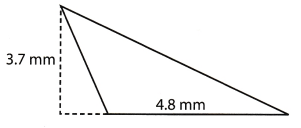
(A) 4.44mm²
(B) 5.92 mm²
(C) 8.88 mm²
(D) 17.76 mm²
Answer:
(C) 8.88 mm²

Explanation:
Determine the area of the triangle
A = \(\frac{1}{2}\) ∙ 4.8 ∙ 3.7 substitute for the given values
A = \(\frac{17.76}{2}\) simplify
A = 8.88 mm² area of the triangle
The area of the triangle is 8.88 mm².

Question 3.
A rectangular prism has a volume of 912 cubic meters. It has a length of 19 meters and a width of 12 meters. Which equation could be solved to find the height of the rectangular prism?
(A) 114h = 912
(B) 228h = 912
(C) 15.5h = 912
(D) 31h = 912
Answer:
(B) 228h = 912

Explanation:
Determine the height of the rectangular prism.
V = lwh formula for the volume of the rectangular prism
912 = 19 ∙ 12 ∙ h substitute for the given values
912 = 228h simplify
4 meters = h volume of the rectangular prism
The equation to be used in solving the height of the rectangular prism is 228h = 912.

Question 4.
The trapezoid below has an area of 1,575 cm².

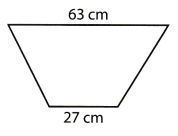
Which equation could you solve to find the height of the trapezoid?
(A) 45h = 1,575
(B) 90h = 1,575
(C) 850.5h = 1,575
(D) 1,70h = 1,575
Answer:
(A) 45h = 1,575

Explanation:
What is the height of the trapezoid?
A = \(\frac{1}{2}\)h(b₁ + b₂) Write the formula
1575 = \(\frac{1}{2}\) h(63 + 27) Use the formula to write an equation
1575 = \(\frac{1}{2}\) h(90) Add inside parentheses
1575 = 45h Multiply \(\frac{1}{2}\) and 90

Gridded Response

Question 5.
Cindy is designing a rectangular fountain in a courtyard. The rest of the courtyard will be covered in stone.

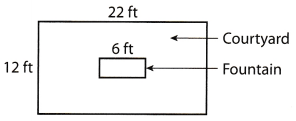
The part of the courtyard that will be covered in stone has an area of 246 ft². What is the width of the fountain in feet?

Answer:
Determine the area of the whole courtyard.
A = l × w formula for the area of a rectangle
A = 22 × 12 substitute for the given values
A = 264 ft² area of the whole courtyard
Subtract the area of the courtyard covered in stone from the whole courtyard.
A = 264 – 246 substitute for the given values
A = 18 ft² area of the fountain

Determine the width of the fountain.
A = l × w formula for the area of a rectangle
18 = 6w substitute for the given values
\(\frac{18}{6}=\frac{6 w}{6}\) divide both sides of the equation by 6
3 ft = w width of the fountain
The gridded response is 3.00 ft which is the width of the fountain.