Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 17.1 Answer Key Measures of Center.
Texas Go Math Grade 6 Lesson 17.1 Answer Key Measures of Center
Essential Question
How can you use measures of center to describe a data set?
Texas Go Math Grade 6 Lesson 17.1 Explore Activity Answer Key
Explore Activity 1
Finding the Mean
A measure of center is a single number used to describe a set of numeric data. A measure of center describes a typical value from the data set.
One measure of center is the mean. The mean, or average, of a data set is the sum of the data values divided by the number of data values in the set.
Tami surveyed five of her friends to find out how many brothers and sisters they have. Her results are shown in the table.

A. Model each person’s response as a group of counters.

B. Now rearrange the counters so that each group has the same number of counters.
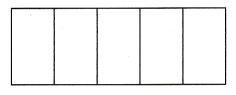
Each group now has ________ counter(s). This value is the mean. This model demonstrates how the mean “evens out” the data values.
C. Use numbers to calculate the mean.
The sum of the data values is 
How many data values are in the set? ________

Math Talk
Mathematical Processes
Suppose you have a data set in which all of the values are 2. What is the mean?
Reflect
Question 1.
Can the mean be greater than the greatest value in a data set? Why or why not?
Answer:
No, because the group with the greatest amount will share its counters to ‘even out’ the data
Reflect
Question 2.
What If? Which units are used for the data in A ? if the coach had recorded some distances in kilometers and some in miles, can you still find the median of the data? Explain.
Answer:
The unit used for recording the distance is miles.
If the coach had recorded some distances in kilometers and some in miles, then the median could not be evaluated because the unit of the data set must be same.
Your Turn
Question 3.
Charlotte recorded the number of minutes she spent exercising in the past ten days: 12, 4, 5, 6, 8, 7, 9, 8, 2, 1. Find the median of the data.
Answer:
Data set:
12, 4, 5, 6, 8, 7, 9, 8, 2, 1
Arrarge the data set in ascending order:
= 1, 2, 4, 5, 6, 7, 8, 8, 9, 12
Determine the average/mean of the middle values of the data set arranged in ascending order, therefore:
Median = \(\frac{6+7}{2}\) = 6.5
Median = 6.5 minutes
Explore Activity 2
Comparing the Mean and the Median
The mean and median of a data set may be equal, very close to each other, or very different from each other. For data sets where the mean and median differ greatly, one likely describes the data set better than the other.
The monthly earnings of several teenagers are $200, $320, $275, $250, $750, $350, and $310.

A. Find the mean.

B. Write the data values in order from least to greatest and find the median.
C. The mean and the median differ by about $__. why?
D. Which measure of center better describes the typical monthly earnings for this group of teenagers—the mean or the median? Explain.
Reflect
Question 4.
Communicate Mathematical Ideas Luka’s final exam scores for this semester are 70, 72, 99, 72, and 69. Find the mean and median. Which is a better description of Luka’s typical exam score? Explain your thinking.
Answer:
70, 72, 99, 72, 69
Arrange the data set in ascending order:
= 69, 70, 72, 72, 99
Determine the middle value of the data set arranged in ascending order, therefore:
Median = 72
Evaluate the mean of the data set:
Median = \(\frac{69+70+72+72+99}{5}\) = 76.4
Median is a better representation of the data set because 4 out of his 5 scores are around the 69 to 72 range.
Texas Go Math Grade 6 Lesson 17.1 Guided Practice Answer Key
Question 1.
Spencer surveyed five of his friends to find out how many pets they have. His results are shown in the table. What is the mean number of pets? (Explore Activity 1)

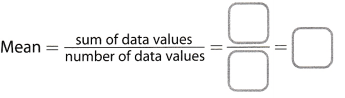
The mean number of pets is ___
Answer:
Evaluate mean of the given data:
Mean = \(\frac{3+5+2+4+1}{5}\) = 3
The mean number of pets is 3.
Question 2.
The following are the weights, in pounds, of some dogs at a kennel: 36,45, 29, 39, 51,49. (Example 1)
a. Find the median. ____
Answer:
Data set:
36, 45, 29, 39, 51, 49
Arrange the data set in ascending order:
= 29, 36, 39, 45, 49, 51
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
Median = \(\frac{39+45}{2}\) = 42
Median weight is 42 pounds.
b. Suppose one of the weights were given in kilograms. Can you still find the median? Explain.
Answer:
The unit of the data set must be same. If 1 value was in kilograms, then it should be converted to an equivalent weight in pounds before the evaluation of the mean. The mean in this case can not directly be calculated.
Question 3.
a. Find the mean and the median of this data set: 9, 6, 5, 3, 28, 6, 4, 7. (Explore Activity 2)
Answer:
Ascending order of the data: 3, 4, 5, 6, 6, 7, 9, 28.

The mean is 8.5 whiLe the median is 6.
b. Which better describes the data set, the mean or the median? Explain.
Answer:
Median describes the data set better because the values are much nearer to the value of the median than the mean.
Median
Essential Question Check-In
Question 4.
How can you use measures of center to describe a data set?
Answer:
Measures of center is used to describe the trend in a certain data set. The 2 types of measures are mean and median. Median is usually a better representation of a data set because mean is affected by extreme values.
Texas Go Math Grade 6 Lesson 17.1 Independent Practice Answer Key
Several students in Ashton’s class were randomly selected and asked how many text messages they sent yesterday. Their answers were 1, 0, 10, 7, 13, 2, 9, 15, 0, 3.
Question 5.
How many students were asked? How do you know?
Answer:
The number of responses are 10. This implies that 10 students were asked.
10 students were asked.
Question 6.
Find the mean and the median for these data. Mean = ____ Median = ____
Answer:
Data set:
1, 0, 10, 7, 13, 2, 9, 15, 0, 3
Arrange the data set in ascending order:
= 0, 0, 1, 2, 3, 7, 9, 10, 13, 15
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
Median = \(\frac{3+7}{2}\) = 5
Median number of texts is 5.
Evaluate mean of the data:
Mean = \(\frac{0+0+1+2+3+7+9+10+13+15}{10}\)
Evaluate:
Mean = 6
Mean number of texts is 6
Median = 5
Mean = 6
The points scored by a basketball team in its last 6 games are shown. Use these data for 7 and 8.
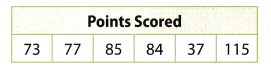
Question 7.
Find the mean score and the median score.
Mean = ___ Median = ___
Answer:
Data set:
73, 77, 85, 84, 37, 115
Arrange the data set in ascending order:
= 37, 73, 77, 84, 85, 115
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
Median = \(\frac{77+84}{2}\) = 80.5
Evaluate mean of the data:
Mean = \(\frac{73+77+85+84+37+115}{6}\)
Evaluate:
Mean = 78.5
Question 8.
Which measure better describes the typical number of points scored? Explain.
Answer:
Median = 80.5 is a better representation of the points scored as this is closest to most of the numbers in the data set, because the extreme values of 37 and 115 have affected the central tendency of the data set.
Median.
Some people were asked how long it takes them to commute to work. Use the data for 9-11.
Question 9.
What units are used for the data? What should you do before finding the mean and median number of minutes?

Answer:
2 different units are used here. Therefore, convert the times given in hours to minutes for the evaluation of mean and median, so 0.5 hours = 0.5 × 60 = 30 minutes and 1 hour = 60 minutes.
Question 10.
Find the mean and median number of minutes.
Mean = ___ Median = ____
Answer:
Data set:
16, 7, 14, 30, 5, 8, 12, 60
Arrange the data set in ascending order:
= 5, 7, 8, 12, 14, 16, 30, 60
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
Median = \(\frac{12+14}{2}\) = 13
Evaluate mean of the data:
Mean = \(\frac{16+7+14+30+5+8+12+60}{8}\)
Evaluate
Mean = 19
Question 11.
Which measure do you think is more typical of the data?
Answer:
It can be seen that most members of the data set are less than or equal to 16, therefore, 13 = median is a more typical measure of the data set. It can also be seen that mean here is affected by the commutes of 30 and 60 minutes, increasing it to 19 minutes, which in this scenario, does not make sense.
Median.
Texas Go Math Grade 6 Lesson 17.1 H.O.T. Focus On Higher Order Thinking Answer Key
Question 12.
Critique Reasoning For two weeks, the school librarian recorded the number of library books returned each morning. The data are shown in the dot plot. The librarian found the mean number of books returned each morning.

\(\frac{8+6+10+5+9+8+3+6}{8}\) = \(\frac{55}{8}\) = 6.9
Is this the correct mean of this data set? If not, explain and correct the answer.
Answer:
The number of entries recorded are 10 so the divisor during mean calculation should also be 10. This is the error made here. The correct mean in this context is \(\frac{55}{10}\) = 5.5
Question 13.
Critical Thinking Lauren’s scores on her math tests are 93, 91, 98, 100, 95, 92, and 96. What score could Lauren get on her next math test so that the mean and median remain the same? Explain your answer.
Answer:
Data set:
93, 91, 98, 100, 95, 92, 96
Arrange the data set in ascending order:
= 91, 92, 93, 95, 96, 98, 100
Determine the middle value of the data set arranged in ascending order, therefore:
Median = 95
The next test will be the 8th test so let her score in this test be x, then equation of mean here becomes:

Solve for x:
x + 665 = 8(95)
Evaluate:
x = 760 – 665 = 95
She must score 95 on her 8th test
Question 14.
Persevere in Problem Solving Yuko wants to take a job selling cars. Since she will get a commission for every car she sells, she finds out the sale price of the last four cars sold at each company.
Company A: $16,000; $20,000; $25,000; $35,000;
Company B: $21,000, $23,000, $36,000, $48,000
a. Find the mean selling price at each company.
Answer:
Evaluate mean of the data for A:
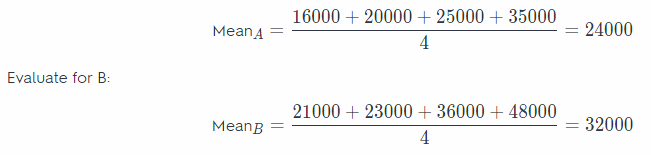
b. Find the median selling price at each company.
Answer:
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
MedianA = \(\frac{20000+25000}{2}\) = 22500
Determine the mean of the 2 middle values of the data set arranged in ascending order, therefore:
MedianB = \(\frac{23000+36000}{2}\) = 29500
c. Communicate Mathematical Ideas At either company, Yuko will get paid a commission of 20% of the sale price of each car she sells. Based on the data, where do you recommend she take a job? Why?
Answer:
She should work in company B because both the median and mean price of cars sold there are more than that of A. The more the amount of cars sold, the greater is the commission.