Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 16.3 Answer Key Solving Area Equations.
Texas Go Math Grade 6 Lesson 16.3 Answer Key Solving Area Equations
Example 1
The Hudson High School wrestling team just won the state tournament and has been awarded a triangular pennant to hang on the wall in the school gymnasium. The base of the pennant is 1.5 feet long. It has an area of 2.25 square feet. What is the height of the pennant?

The height of the pennant is 3 feet.
Your Turn
Question 1.
Renee is sewing a quilt whose pattern contains right triangles. Each quilt piece has a height of 6 in. and an area of 24 in2. How long is the base of each quilt piece? ___________
Answer:
Data:
Area = 24
h = 6
Write equation of area of a triangle:
Area = \(\frac{1}{2}\) × b × h
Solve for b:
b = \(\frac{2 \times \text { Area }}{h}\)
Substitute values:
b = \(\frac{2 \times 24}{6}\)
Evaluate:
b = 8
The base of the quilt is 8 inches long.
Example 2
A garden in the shape of a trapezoid has an area of 44.4 square meters. One base is 4.3 meters and the other base is 10.5 meters long. The height of the trapezoid is the width of the garden. How wide is the garden?

The garden is 6 meters wide.
Reflect
Question 2.
Communicate Mathematical Ideas Explain why the first step after substituting is addition.
Answer:
The numbers in the parentheses are added because parentheses simplification has the highest priority and that rule is followed after substitution.
Your Turn
Question 3.
The cross section of a water bin is shaped like a trapezoid. The bases of the trapezoid are 18 feet and 8 feet long. It has an area of 52 square feet. What is the height of the cross section?
Answer:
What is the height of the cross section?
A = \(\frac{1}{2}\) h(b1 + b2) Write the formula
52 = \(\frac{1}{2}\)h(18 + 8) Use the formula to write an equation
52 = \(\frac{1}{2}\)h(26) Add inside parentheses
52 = 13h Multiply \(\frac{1}{2}\) and 26
\(\frac{52}{13}=\frac{13 h}{13}\) Divide both sides of the equation by 13
4 = h
The height of the cross section is 4 feet long
Question 4.
A parallelogram-shaped field in a park needs sod. The parallelogram has a base of 21.5 meters and a height of 18 meters. The sod is sold in pallets of 50 square meters. How many pallets of sod are needed to fill the field?
Answer:
Data:
b = 21.5
h = 18
Write equation of area of a paralLelogram:
Area = b × h
Substitute values:
Area = 21.5 × 18
Evaluate:
Area = 387
Evaluate the number of pallets of sods, therefore: n = \(\frac{387}{50}\) = 7.74
7.74 ≈ 8 pallets of sods are needed.
Texas Go Math Grade 6 Lesson 16.3 Guided Practice Answer Key
Question 1.
A triangular bandana has an area of 70 square inches. The height of the triangle is 8\(\frac{3}{4}\) inches. Write and solve an equation to find the length of the base of the triangle. (Example 1)
Answer:
Data:
Area = 70
h = 8\(\frac{3}{4}\) = 8.75
Write equation of area of a triangle:
Area = \(\frac{1}{2}\) × b × h
Solve for b:
b = \(\frac{2 \times \text { Area }}{h}\)
Substitute values:
b = \(\frac{2 \times 70}{8.75}\)
Evaluate:
b = 16
Base of the triangle is 16 inches.
Question 2.
The top of a desk is shaped like a trapezoid. The bases of the trapezoid are 26.5 and 30 centimeters long. The area of the desk is 791 square centimeters. The height of the trapezoid is the width of the desk. Write and solve an equation to find the width of the desk. (Example 2)
Answer:
Data:
Area = 791
b1 = 26.5
b2 = 30
Write equation of area of a trapezoid:
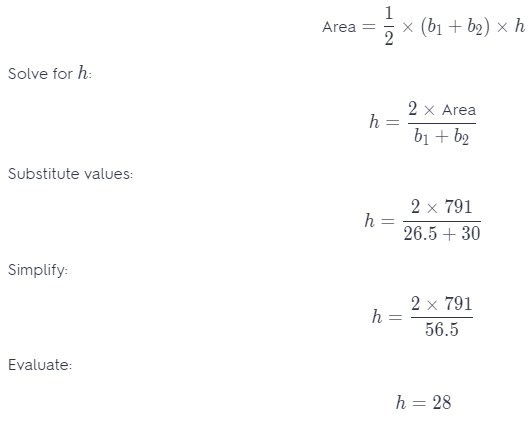
The desk is 28 centimeters wide.
Question 3.
Taylor wants to paint his rectangular deck that is 42 feet long and 28 feet wide. A gallon of paint covers about 350 square feet. How many gallons of paint will Taylor need to cover the entire deck? (Example 3)
Write an equation to find the ______________ of the deck.
Write and solve the equation.
Write an equation to find the ______________.
Write and solve the equation.
Taylor will need ________ gallons of paint.
Answer:
Data:
l = 42
w = 28
Write equation of area of a rectangle:
Area = l × w
Substitute values:
Area = 42 × 28
Evaluate:
Area = 1176
Area of the deck is 1176 square feet.
Evaluate the total number of gallons of paint required by dividing the total area with the area covered by 1 gallon, therefore:
n = \(\frac{1176}{350}\) = 3.364 ≈ 4
Taylor will need 4 gallons of paint.
Essential Question Check-In
Question 4.
How do you use equations to solve problems about area of rectangles, parallelograms, trapezoids, and triangles?
Answer:
Depending on the type of figure given, the respective formula of parallelogram, trapezoid, triangle or rectangle is used to solve such problems.
Texas Go Math Grade 6 Lesson 16.3 Independent Practice Answer Key
Question 5.
A window shaped like a parallelogram has an area of 18\(\frac{1}{3}\) square feet. The height of the window is 3\(\frac{1}{3}\) feet. How long is the base of the window?
Answer:
Data:
h = 3\(\frac{1}{3}\) = \(3 . \overline{3}\)
Area = 18\(\frac{1}{3}\) = \(18 . \overline{3}\)
Write equation of area of a parallelogram:
Area = b × h
Solve for b:
b = \(\frac{\text { Area }}{h}\)
Substitute values:
b = \(\frac{18 . \overline{3}}{3 . \overline{3}}\)
Evaluate:
b = 5.5
The base of the window is 5.5 feet.
Question 6.
A triangular sail has a base length of 2.5 meters. The area of the sail is 3.75 square meters. How tall is the sail?
Answer:
Data:
b = 2.5
Area = 3.75
Write equation of area of a triangle:
Area = \(\frac{1}{2}\) × b × h
Solve for h:
h = \(\frac{2 \times \text { Area }}{b}\)
Substitute values:
h = \(\frac{2 \times 3.75}{2.5}\)
Evaluate:
h = 3
The sail is 3 meters high.
Question 7.
A section in a stained glass window is shaped like a trapezoid. The top base is 4 centimeters and the bottom base is 2.5 centimeters long. If the area of the section of glass is 3.9 square centimeters, how tall is the section?
Answer:
Data:
b1 = 2.5
b2 = 4
Area = 3.9
Write equation of area of a trapezoid:

The section is 1.2 centimeters high.
Question 8.
Multistep Amelia wants to paint three walls in her family room. Two walls are 26 feet long by 9 feet wide. The other wall is 18 feet long by 9 feet wide.
a. What is the total area of the walls that Amelia wants to paint?
Answer:
Data for rectangle 1:
l = 26
w = 9
Data for rectangle 2:
l = 18
w = 9
The totaL area to be painted is the sum of the 3 rectangles out of which 2 are identical so the equation becomes:
Area = 2(l × w) + (l × w)
Substitute values:
Area = 2(26 × 9) + (18 × 9)
Simplify:
Area = 468 + 162
Evaluate:
Area = 630
Total area to be painted in 630 square feet.
b. Each gallon of paint covers about 250 square feet. How many gallons of paint should Amelia buy to paint the walls?
Answer:
For the total number of gallons of paint needed by dividing the total area by the area covered by 1 gallon, therefore:
n = \(\frac{630}{250}\) = 2.52 ≈ 3
Question 9.
Critical Thinking The area of a triangular block is 64 square inches. If the base of the triangle is twice the height, how long are the base and the height of the triangle?
Answer:
Data:
h = x
b = 2x
Area = 64
Write equation of area of a triangle:
Area = \(\frac{1}{2}\) × b × h
Substitute values:
64 = \(\frac{1}{2}\) × 2x × x
Simplify:
64 = x2
Solve for x:
x = \(\sqrt {64}\)
Evaluate:
x = 8
The height of the triangle is 8 inches while its base is 2 × 8 = 16 inches long.
Question 10.
Multistep Alex needs to varnish the top and the bottom of a dozen rectangular wooden planks. The planks are 8 feet long and 3 feet wide. Each pint of varnish covers about 125 square feet and costs $3.50.
a. What is the total area that Alex needs to varnish?
Answer:
Data:
l = 8
w = 3
Write equation for area of a triangle:
Area = l × w
Substitute values:
Area = 8 × 3
Evaluate:
Area = 24
The area of 1 side is 24 square feet Both sides of the planks are to be painted and there are 12 planks so the total area to be painted is 24 × 2 × 12 = 576.
b. How much will it cost Alex to varnish all the wooden planks?
Answer:
For the total number of pints of varnish needed by dividing the total area by the area covered by 1 pint. therefore:
n = \(\frac{576}{125}\) = 4.608 ≈ 5
5 pints of varnish are needed so the total cost of varnish is 5 × $3.5 = $17.50
Question 11.
Multistep Leia cuts congruent triangular patches with an area of 45 square centimeters from a rectangular piece of fabric that is 18 centimeters long and 10 centimeters wide. How many of the patches can Leia cut from 32 pieces of the fabric?
Answer:
Evaluate the total area of the rectangular piece of fabric, therefore:
Area = l × w = 18 × 10 = 180
There are 32 such pieces, so the total area is 180 × 32 = 5760 square centimeters.
Evaluate the number of triangles that can be made dividing the total area by the area of 1 triangular piece, therefore:
n = \(\frac{5760}{45}\) = 128
128 triangles can be made.
Question 12.
Multistep A farmer needs to buy fertilizer for two fields. One field is shaped like a trapezoid, and the other is shaped like a triangle. The trapezoidal field has bases that are 35 and 48 yards and a height of 26 yards. The triangular field has the same height and a base of 39 yards. Each bag of fertilizer covers 150 square yards. Use a problem solving model to find how many bags of fertilizer the farmer needs to buy.
Answer:
Data of the triangular field:
b = 39
h = 26
Data of the trapezoidal field:
b1 = 35, b2 = 48
h = 26
The total area to be covered with fertilizers is the sum of the 2 areas of the triangle and the trapezoid so write respective formulas:
Area = (\(\frac{1}{2}\) × b × h)+(\(\frac{1}{2}\) × (b1 + b2) × h)
Substitute vaLues:
Area = (\(\frac{1}{2}\) × 39 × 26) + (\(\frac{1}{2}\) × (35 + 48) × 26)
Simplify:
Area = 507 + 1079
Evaluate:
Area = 1586
Total area to be covered with fertiLizer is 1586 square yards.
The total number of bags of fertilizer needed is evaluated by dividing the total area by the area covered by 1 bag, therefore:
n = \(\frac{1586}{150}\) = 10.57 ≈ 11
11 bags of fertilizers are needed.
Question 13.
A tennis court for singles play is 78 feet long and 27 feet wide.
a. The court for doubles play has the same length but is 9 feet wider than the court for singles play. How much more area is covered by the tennis court used for doubles play?
Answer:
Area of a regular sized tennis court is 78 × 27 = 2106 square feet. The doubLes court is 9 feet wider so the area of the doubles court is 78 × (27 + 9) = 2808 square feet Therefore, the area of this court is 2808 – 2106 = 702 square feet more than that of the regular court.
b. The junior court for players 8 and under is 36 feet long and 18 feet wide. How much more area is covered by the tennis court used for singles play than by the junior court?
Answer:
Area of a regular sized tennis court is 78 × 27 = 2106 square feet The area of the juniors court is 36 × 18 = 648 square feet. Therefore, the area of this court is 2106 – 648 = 1458 square feet less than that of the regular court.
c. The court for players 10 and under has the same width but is 18 feet shorter than the court for singles play. How much more area is covered by the tennis court used for singles play?
Answer:
Area of a regular-sized tennis court is 78 × 27 = 2106 square feet. The court for 10 and under is 18 feet shorter so the area of this court is (78 – 18) × 27 = 1620 square feet. Therefore, the area of this court is 2106 – 1620 = 486 square feet less than that of the regular court.
Question 14.
Draw Conclusions The cross-section of a metal ingot is a trapezoid. The cross-section has an area of 39 square centimeters. The top base of the cross-section is 12 centimeters. The length of the bottom base is 2 centimeters greater than the top base. How tall is the metal ingot? Explain.
Answer:
Data:
b1 = 12
b2 = 12 + 2 = 14
Area = 39
Write equation of the area of a trapezoid:

The metal ingot is 3 centimeters tall.
H.O.T. Focus on Higher Order Thinking
Question 15.
Analyze Relationships A mirror is made of two congruent parallelograms as shown in the diagram. The parallelograms have a combined area of 9\(\frac{1}{3}\) square yards. The height of each parallelogram is 1\(\frac{1}{4}\) yards.

a. How long is the base of each parallelogram?
Answer:
Data:
h = 1\(\frac{1}{3}\) = \(1 . \overline{3}\)
Area of 1 parallelogram is therefore:
Area = \(\frac{9 \frac{1}{3}}{2}=4 . \overline{6}\)
Write equation of area of a parallelogram:
Area = b × h
Solve for b;
b = \(\frac{\text { Area }}{h}\)
Substitute values:
b = \(\frac{4 . \overline{6}}{1 . \overline{3}}\)
Evaluate:
b = 3.5
The base of the parallelogram shown is 3.5 yards
b. What is the area of the smallest rectangle of wall that the mirror could fit on?
Answer:
The smallest rectangle of wall that the mirror could fit on must have the width equal to the base of the parallelogram and length equal to the height of the parallelogram plus the extra \(\frac{1}{2}\) = 0.5 yards so the length becomes: \(1 . \overline{3}\) + 0.5 = \(1.8 \overline{3}\) so the area of the wall is 3.5 × \(1.8 \overline{3}\) = 6.42 square yards.
Question 16.
Persevere in Problem Solving A watercolor painting is 20 inches long by 9 inches wide. Ramon makes a mat that adds a 1-inch-wide border around the painting. What is the area of the mat?
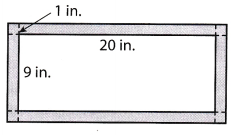
Answer:
The length of the mat plus the painting is 1 + 20 + 1 = 22 inches and its width is 1 + 9 + 1 = 11 inches so the area of the mat pLus the painting is 22 × 11 = 242 square inches.
The length of the painting is 20 inches and its width is inches so the area of the painting is 20 × 9 = 180 square inches. The area of the mat is therefore: 242 – 180 = 62 square inches.
The area of the mat is 62 square inches.