Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 15.1 Answer Key Determining When Three Lengths Form a Triangle.
Texas Go Math Grade 6 Lesson 15.1 Answer Key Determining When Three Lengths Form a Triangle
Essential Question
How can you use the relationship between side lengths to determine when three lengths form a triangle?
Texas Go Math Grade 6 Lesson 15.1 Explore Activity Answer Key
Explore Activity
Drawing Three Sides
Use geometry software to draw a triangle whose sides have the following lengths: 2 units, 3 units, and 4 units.
A. Draw three line segments of 2, 3, and 4 units of length.
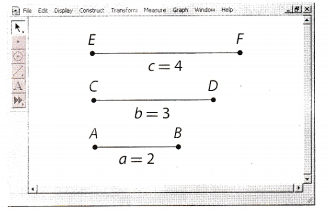
B. Let \(\overline{A B}\) be the base of the triangle. Place endpoint C on top of endpoint B and endpoint E on top of endpoint A. These will become two of the vertices of the triangle.
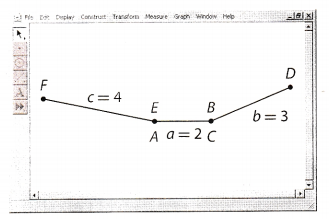
C. Using the endpoints C and E as fixed vertices, rotate endpoints F and D to see if they will meet in a single point.
The line segments of 2, 3, and 4 units  form a triangle.
form a triangle.
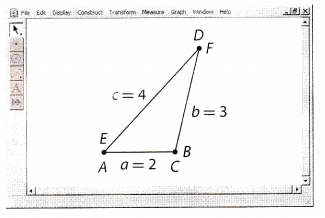
D. Repeat Steps 2 and 3, but start with a different base length. Do the line segments make the exact same triangle as the original?
The line segments  make the same triangle as the original.
make the same triangle as the original.
E. Draw three line segments of 2, 3, and 6 units. Can you form a triangle with the given segments?
The line segments of 2, 3, and 6 units  form a triangle.
form a triangle.
Reflect
Question 1.
Conjecture Try to make triangles using real world objects such as three straws of different lengths. Find three side lengths that form a triangle and three side lengths that do not form a triangle. What do you notice about the lengths that do not form a triangle?
Answer:
The lengths of the line segments of figure 2 triangle do not meet that it cannot form a triangle.

The lengths of the line segments do not meet to form a triangle.
Your Turn
Tell whether a triangle can have sides with the given lengths. Explain.
Question 2.
3 cm, 6 cm, 9 cm
Answer:
Find the sum of the two sides of the triangle then compare to the third side.
3 + 6 > 9 add the two sides and compare to the third side
9 ≯ 9 the sum of the two sides is NOT greater than the third side
6 + 9 > 3 add the two sides and compare to the third side
15 > 3 the sum of the two sides is greater than the third side
3 + 9> 6 add the two sides and compare to the third side
12 > 6 the sum of the two sides is greater than the third side
The given side lengths cannot form a triangle because the sum of two side lengths is not greater than the third side.
Question 3.
4m, 5m, 8m
Answer:
Find the sum of the two sides of the triangle then compare to the third side.
4 + 5 > 8 add the two sides and compare to the third side
9 > 8 the sum of the two sides is greater than the third side
5 + 8 > 4 add the two sides and compare to trie third side
13 > 4 the sum of the two sides is greater than the third side
4 + 8 > 5 add the two sides and compare to the third side
12 > 5 the sum of the two sides is greater than the third side
The given side lengths can form a triangle because the sum of two side lengths is greater than the third side.
Your Turn
Question 4.
Which value could be the length of x?
x = 35 x = 13
_______
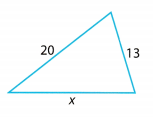
Answer:
Determine the value of x.

The length of the third side of the triangle must be 13.
Texas Go Math Grade 6 Lesson 15.1 Guided Practice Answer Key
Determine whether a triangle can have sides with the given length Explain. (Explore Activity and Example 1)
Question 1.
3 cm, 10 cm, 8 cm
Answer:
Find the sum of the two sides of the triangle then compare to the third side.
3 + 10> 8 add the two sides and compare to the third side
13 > 8 the sum of the two sides is greater than the third side
10 + 8 > 3 add the two sides and compare to the third side
18 > 3 the sum of the two sides is greater than the third side
3 + 8 > 10 add the two sides and compare to the third side
11 > 10 the sum of the two sides is greater than the third side
The given lengths can make up a triangle.
Question 2.
10 ft, 10 ft, 18 ft
Answer:
Find the sum of the two sides of the triangLe then compare to the third side.
10 + 10 > 18 add the two sides and compare to the third side
20 > 18 the sum of the two sides is greater than the third side
10 + 18 > 10 add the two sides and compare to the third side
28 > 10 the sum of the two sides is greater than the third side
10 + 18 > 10 add the two sides and compare to the third side
28 > 10 the sum of the two sides is greater than the third side
The given lengths can be used to make a triangle.
Question 3.
30 in., 20 in., 40 in.
Answer:
Find the sum of the two sides of the triangle then compare to the third side.
30 + 20> 40 add the two sides and compare to the third side
50 > 40 the sum of the two sides is greater than the third side
20 + 40> 30 add the two sides and compare to the third side
60 > 30 the sum of the two sides is greater than the third side
30 + 40 > 20 add the two sides and compare to the third side
70 > 20 the sum of the two sides is greater than the third side
The given lengths can be used to make a triangle.
Question 4.
16 cm, 12 cm, 3 cm
Answer:
Find the sum of the two sides of the triangle then compare to the third side.
16 + 12 > 3 add the two sides and compare to the third side
28 > 3 the sum of the two sides ¡s greater than the third side
12 + 3 > 16 add the two sides and compare to the third side
15 ≯ 16 the sum of the two sides is NOT greater than the third side
16 + 3 > 12 add the two sides and compare to the third side
19 > 12 the sum of the two sides is greater than the third side
The given lengths cannot be used to make a triangle.
Question 5.
Which value could be the length of x? (Example 2)
x = 29 x = 45
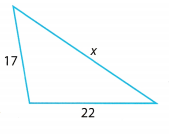
Answer:
Determine the value of x.

The length of the third side must be 29.
Essential Question Check-In
Question 6.
Explain how you can determine whether three metal rods can be joined to form a triangle.
Answer:
- Measure the Lengths of the given metal rods.
- Find the sum of the two lengths of the metal rods.
- Compare the sum of the two lengths to the third length.
- If the sum of the two lengths is greater than the third length, then it can be joined to form a triangle.
Get the lengths of the metal rods and find the sum of the two lengths. If the sum is greater than the third length, then it can be a triangle.
Texas Go Math Grade 6 Lesson 15.1 Independent Practice Answer Key
Question 7.
A map of a new dog park shows that it is triangular and that the sides measure 18.5 m, 36.9 m, and 16.9 m. Are the dimensions correct? Explain your reasoning.
Answer:
Find the sum of the two sides of the triangLe then compare to the third side.
18.5 + 36.9 > 16.9 add the two sides and compare to the third side
55.4 > 16.9 the sum of the two sides is greater than the third side
18.5 + 16.9 > 36.9 add the two sides and compare to the third side
35.4 ≯ 36.9 the sum of the two sides is NOT greater than the third side
36.9 + 16.9> 18.5 add the two sides and compare to the third side
53.8 > 18.5 the sum of the two sides is greater than the third side
The dimensions are not correct because the sum of two sides, 18.5 and 16.9 is not greater than the third side which is 36.9.
Question 8.
Choose a real world object that you can cut into three different lengths to form a triangle. Find three side lengths that form a triangle and three lengths that do not form a triangle. For each triangle, give the side lengths and explain why those lengths do or do not form a triangle.
Triangle 1: __________________________
Triangle 2: __________________________
Answer:
- Triangle 1: Cotton bud with side lengths of 2 mm, 3 mm, and 4 mm.
2 + 3 > 4 add the two sides and compare to the third side
5 > 4 the sum of the two sides is greater than the third side
2 + 4 > 3 add the two sides and compare to the third side
6 > 3 the sum of the two sides is greater than the third side
3 + 4 > 2 add the two sides and compare to the third side
7 > 2 the sum of the two sides is greater than the third side
- Triangle 2: Barbecue stick with side lengths of 5 cm,1 cm, and 3 cm.
5 + 3 > 1 add the two sides and compare to the third side
8 > 1 the sum of the two sides is greater than the third side
5 + 1 > 3 add the two sides and compare to the third side
6 > 3 the sum of the two sides is greater than the third side
3 + 1 > 5 add the two sides and compare to the third side
4 ≯ 5 the sum of the two sides is NOT greater than the third side
Triangle 1 with side lengths of 2 mm, 3 mm, and 4 mm can for a triangle.
Triangle 2 with side lengths of 5 cm, 1 cm, and 3 cm cannot form a triangle because the sum of the two sides, 3 and 1, is not greater than the third side, 5.
Question 9.
Could the three sides of a triangular shopping mall measure \(\frac{1}{2}\) mi, \(\frac{1}{3}\) mi and \(\frac{1}{4}\) mi? Show how you found your answer.
Answer:
Find the sum of the two sides of the triangle then compare to the third side

Yes, the side lengths can be the dimensions of a triangular shopping mall.
Question 10.
Geography The map shows the distance in air miles from Flouston to both Austin and San Antonio.
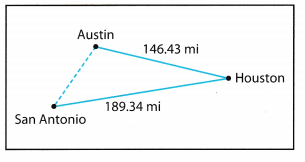
a. What is the greatest possible distance from Austin to San Antonio?
Answer:
b. How did you find the answer?
Answer:
c. What is the least possible distance from Austin to San Antonio?
Answer:
d. How did you find the answer?
Answer:
Question 11.
Critical Thinking Two sides of an isosceles triangle measure 3 inches and 13 inches respectively. Find the length of the third side. Explain your reasoning.
Answer:
Determine if the length of the third side is 3 inch or 13 inch.
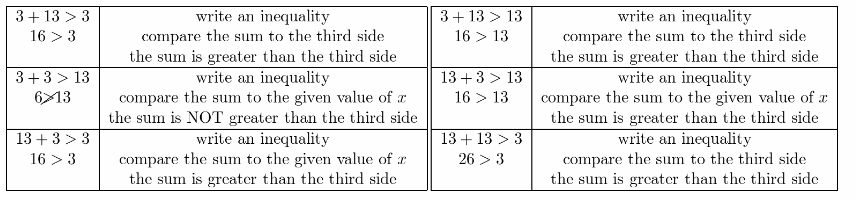
The length of the third side of an isosceles triangle is 13 inches.
Texas Go Math Grade 6 Lesson 15.1 H.O.T. Focus On Higher Order thinking Answer Key
Question 12.
Critique Reasoning While on a car trip with her family, Erin saw a sign that read, “Amarillo 100 miles, Lubbock 80 miles.” She concluded that the distance from Amarillo to Lubbock is 100 – 80 = 20 miles. Was she right? Explain.
Answer:
Question 13.
Make a Conjecture Is there a value of n for which there could be a triangle with sides of length n, 2n, and 3n? Explain.
Answer:
Find the sum of two sides of the triangle and compare to the third side.
n + 2n > 3n add the two sides and compare to the third side
3n ≯ 3n the sum of the two sides is NOT greater than the third side
2n + 3n> n add the two sides and compare to the third side
5n > n the sum of the two sides is greater than the third side
n + 3n > 2n add the two sides and compare to the third side
4n > 2n the sum of the two sides is greater than the third side
There is no value for n which can be a side for the length of the triangle based on the solution.
Question 14.
Persevere in Problem Solving A metalworker cut an 8-foot length of pipe into three pieces and welded them to form a triangle. Each of the 3 sections measured a whole number of feet in length. How long was each section? Explain your reasoning.
Answer:
Determine the sides of the triangle using an 8-foot length pipe.
3 + 2 > 3 add the two sides and compare to the third side
5 > 3 the sum of the two sides is greater than the third side
2 + 3 > 3 add the two sides and compare to the third side
5 > 3 the sum of the two sides is greater than the third side
3 + 3 > 2 add the two sides and compare to the third side
6 > 2 the sum of the two sides is greater than the third side
The length of each sections are 3 ft, 2 ft. and 3 ft because when the length of the two sides are added, the sum ¡s greater than the length of the third side.