McGraw Hill Math Grade 5 Chapter 10 Lesson 12 Answer Key Finding the Volume of Irregular Solids

by

All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 10 Lesson 12 Finding the Volume of Irregular Solids are as per the latest syllabus guidelines.

McGraw-Hill Math Grade 5 Answer Key Chapter 10 Lesson 12 Finding the Volume of Irregular Solids

Calculate

Find the volume of each object.

Question 1.
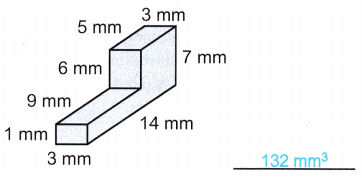
McGraw Hill Math Grade 5 Chapter 10 Lesson 12 Answer Key Finding the Volume of Irregular Solids 46

Question 2.
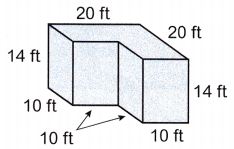
McGraw Hill Math Grade 5 Chapter 10 Lesson 12 Answer Key Finding the Volume of Irregular Solids 47
Answer:
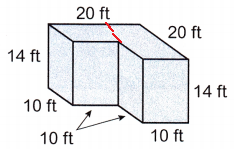
McGraw-Hill-Math-Grade-5-Chapter-10-Lesson-12-Answer-Key-Finding-the-Volume-of-Irregular-Solids-47
Explanation:
First we have to separate the given object into two solids then we have to find the volume of each solid.
Volume of one solid:
Length (l) = 10 feet
Width (w) = 10 feet
height (h) = 14 feet
Volume (v) = (l x w) x h
v = (10 ft x 10 ft) x 14 ft
v = 1,400 cubic feet
Volume of another solid:
Length (l) = 20 feet
Width (w) = 10 feet
height (h) = 14 feet
Volume (v) = (l x w) x h
v = (20 ft x 10 ft) x 14 ft
v =2,800 cubic feet
Now we have to add the two volumes.
1,400 cubic feet +2,800 cubic feet = 4,200 cubic feet
The volume of the object is 4,200 cubic feet.

Question 3.
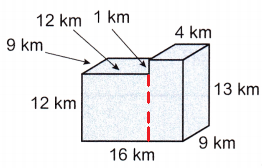
McGraw Hill Math Grade 5 Chapter 10 Lesson 12 Answer Key Finding the Volume of Irregular Solids 48
Answer:
McGraw-Hill-Math-Grade-5-Chapter-10-Lesson-12-Answer-Key-Finding-the-Volume-of-Irregular-Solids-48
Explanation:
First we have to separate the given object into two solids then we have to find the volume of each solid.
Volume of one solid:
Length (l) = 12 km
Width (w) = 9 km
height (h) = 12 km
Volume (v) = (l x w) x h
v = (12 km x 9 km) x 12 km
v = 1,296 cubic kilometer
Volume of another solid:
Length (l) = 4 km
Width (w) = 9 km
height (h) = 13 km
Volume (v) = (l x w) x h
v = (4 km x 9 km) x 13 km
v =468 cubic kilometer
Now we have to add the two volumes.
1,296 cubic kilometer + 468 cubic kilometer = 1,764 cubic kilometer
The volume of the object is 1,764 cubic kilometer.

Question 4.
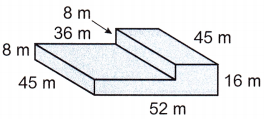
McGraw Hill Math Grade 5 Chapter 10 Lesson 12 Answer Key Finding the Volume of Irregular Solids 49
Answer:
McGraw-Hill-Math-Grade-5-Chapter-10-Lesson-12-Answer-Key-Finding-the-Volume-of-Irregular-Solids-49

Explanation:
First we have to separate the given object into two rectangular prisms then we have to find the volume of each solid.
Volume of one rectangular prism:
Length (l) = 45 m
Width (w) = 36 m
height (h) = 8 m
Volume (v) = (l x w) x h
v = (45 m x 36 m) x 8 m
v = 12,960 cubic meters
Volume of another rectangular prism:
Length (l) = 45 m
Width (w) = 16 m
height (h) = 16 m
Volume (v) = (l x w) x h
v = (45 m x 16 m) x 16 m
v = 11,520 cubic meters
Now we have to add the two volumes.
12,960 cubic meters + 11,520 cubic meters = 24,480 cubic meters
The volume of the object is 24,480 cubic meters.

Leave a Comment