Texas Go Math Grade 8 Lesson 9.2 Answer Key Volume of Cones

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 9.2 Answer Key Volume of Cones.

Texas Go Math Grade 8 Lesson 9.2 Answer Key Volume of Cones

Texas Go Math Grade 8 Lesson 9.2 Explore Activity Answer Key

Modeling the Volume of a Cone

A cone is a three-dimensional figure that has one vertex and one circular base.

To explore the volume of a cone, Sandi does an experiment with a cone and a cylinder that have congruent bases and heights. She fills the cone with popcorn kernels and then pours the kernels into the cylinder. She repeats this until the cylinder is full.

Sandi finds that it takes 3 cones to fill the volume of the cylinder.
STEP 1: What is the formula for the volume V of a cylinder with base area B and height h? __________
STEP 2: What is the area of the base of the cone? __________
STEP 3: Sandi found that, when the bases and height are the same, __________ times V_cone = V_cylinder.
STEP 4: How does the volume of the cone compare to the volume of the cylinder?
Volume of cone: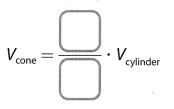

Reflect

Question 1.
Use the conclusion from this experiment to write a formula for the volume of a cone in terms of the height and the radius. Explain.
Answer:
From the experiment we found that:
V_cone = \(\frac{1}{3}\) V_cylinder
Therefore,
V_cone = \(\frac{1}{3}\)πr²h
where r is the radius of the base of the cone and h is the height of the cone.

Question 2.
How are the formulas for the volume of a cone and a pyramid similar?
Answer:
Find the simiLarity and difference between the pyramid and the cone and theirs voLumes. Also notice what type of a base have the pyramid and the cone. Make conclusions based on that.
Volume of Pyramid or Cones = \(\frac{1}{3}\) × Area of Base × height = \(\frac{1}{3}\)Bh
The volume of three cones is equal to the volume of one cylinder with the same base and height. Similarly, the volume of three pyramids is real to the volume of one prism with the same base and height.
Difference in the volume of pyramid and cone is in base.
The base of a cone is a circle which formula is B = πr²
The base of a pyramid is a square.
Formulas for the volume of a cone and a pyramid is \(\frac{1}{3}\)Bh

Example 1

Find the volume of each cone. Round your answers to the nearest tenth. Use 3.14 for π.

The volume is about 150.7 ft³.

Reflect

Question 3.
How can you rewrite the formula for the volume of a cone using the diameter d instead of the radius r?
Answer:
The volume of the cone is given as:
V = \(\frac{1}{3}\)πr²h ……….. (1)
On the other hand, the relation between the radius r and the diameter d can be expressed as:
r = \(\frac{d}{2}\) ………….. (2)
Substituting (2) into (1) so that we can rewrite the formula for the volume of a cone using the diameter d instead of the radius r:
V = \(\frac{1}{3}\)πr²h
V = \(\frac{1}{3}\) ∙ π ∙ (\(\frac{d}{2}\))² ∙ h
V = \(\frac{1}{3}\) ∙ π ∙ \(\frac{d^{2}}{4}\) ∙ h
V = \(\frac{1}{12}\) ∙ π ∙ d² ∙ h

Your Turn

Find the volume of each cone. Round your answers to the nearest tenth. Use 3.14 for π.

Question 4.

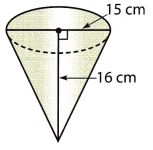
Answer:
The diameter d of the base of the cone is 15 cm, therefore the radius r is 75 cm. The height h of the cone is 16 cm.
V = \(\frac{1}{3}\)πr²h
V = \(\frac{1}{3}\) ∙ 3.14 ∙ (7.5)² ∙ 16
V = 942
The volume of the cone is 942 cm³

Question 5.

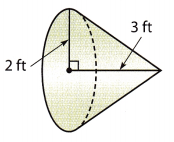
Answer:
Here, radius is 2ft and height is 3 ft.
volume of the cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 2² × 3
= 12.56 ft³

Example 2

For her geography project, Karen built a clay model of a volcano in the shape of a cone. Her model has a diameter of 12 inches and a height of 8 inches. Find the volume of clay in her model to the nearest tenth. Use 3.14 for π.

STEP 1: Find the radius.
r = \(\frac{12}{2}\) = 6 in.
STEP 2: Find the volume of clay.

The volume of the clay is about 301.4 in³.

Your Turn

Question 6.
The cone of the volcano Paricutin in Mexico had a height of 410 meters and a diameter of 424 meters. Approximate the volume of the cone.
Answer:
Here, height of the volcano = 410 meters and the diameter is 424 meters.
the radius of the volcano is 424/2 = 212 meters
volume of the cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 212² × 410
= 19286968.53 m³

Texas Go Math Grade 8 Lesson 9.2 Guided Practice Answer Key

Question 1.
The area of the base of a cylinder is 45 square inches and its height is 10 inches. A cone has the same area for its base and the same height. What is the volume of the cone? (Explore Activity)

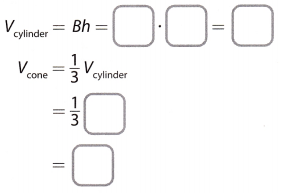
The volume of the cone is ___________ in³.
Answer:
The area of the base of a cylinder, B = 45 in²
Height of the cylinder, h = 10 inch
Volume of the cylinder, V_cylinder = B × h
= 45 × 10 = 450 inch³
Volume of the cone, V_cone = \(\frac{1}{3}\)V_cylinder
= \(\frac{1}{3}\)(450 inch³) = 150 inch³
So, the volume of the cone is
V_cone = 150 in³

Question 2.
A cone and a cylinder have congruent height and bases. The volume of the cone is 18 m³. What is the volume of the cylinder? Explain. (Explore Activity)
Answer:
The volume of the cone is 18 m³. We know that:
V_cone = \(\frac{1}{3}\)V_cylinder
V_cylinder = 3V_cone
V_cylinder = 3 ∙ 18
V_cylinder = 54 m³

Find the volume of each cone. Round your answer to the nearest tenth if necessary. Use 3.14 for π. (Example 1)

Question 3.

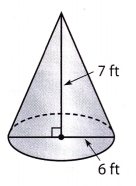
Answer:
The diameter of the cone is 6 ft.
so, the radius of the cone is 3 ft
the height of the cone is 7 ft.
the volume of cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 3² × 7
= 65.94 ft³

Question 4.

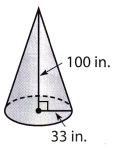
Answer:
Here, the radius is 33 inch and the height is 100 inch
volume of cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 33² × 100
= 113982 in³

Question 5.
Gretchen made a paper cone to hold a gift for a friend. The paper cone was 15 inches high and had a radius of 3 inches. Find the volume of the paper cone to the nearest tenth. Use 3.14 for π. (Example 2)
Answer:
Here, the radius is 3 inch and the height is 15 inch
volume of cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 3² × 15
= 141.3 in³

Question 6.
A cone-shaped building is commonly used to store sand. What would be the volume of a cone-shaped building with a diameter of 50 meters and a height of 20 meters? Round your answer to the nearest tenth. Use 3.14 for π. (Example 2)
Answer:
The diameter of the cone is 50 meters.
so, the radius of the cone is 25 meters.
the height of the cone is 20 meters.
the volume of cone = \(\frac{1}{3}\) × π × r² × h
= \(\frac{1}{3}\) × 3.14 × 25² × 20
= 13083.33 m³

Essential Question Check-In

Question 7.
How do you find the volume of a cone? For help, use the model in the Explore Activity.
Answer:
V_cone = \(\frac{1}{3}\)V_cylinder
V_cone = \(\frac{1}{3}\)πr²h

Texas Go Math Grade 8 Lesson 9.2 Independent Practice Answer Key

Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 8.

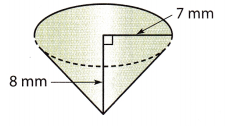
Answer:
Radius r = 7 mm
Height = 8 mm
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (7)² × 8
Volume = 410.29 mm³
Volume ≈ 410.3 mm³

Question 9.

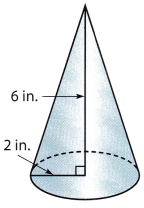
Answer:
Radius r = 2 in
Height = 6 in
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (2)² × 6
Volume = 25.12 in³
Volume ≈ 25.1 in³

Question 10.
A cone has a diameter of centimeters and a height of 11.5 centimeters.
Answer:
Diameter of base = 6 cm
Radius = \(\frac{6}{2}\) cm
Radius r = 3 cm
Height = 11.5 cm
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (3)² × 11.5
Volume = 108.33 cm³
Volume ≈ 108.3 cm³

Question 11.
A cone has a radius of 3 meters and a height of 10 meters.
Answer:
Radius r = 3 m
Height = 10 m
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (3)² × 10
Volume = 94.2 m³

Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 12.
Antonio is making mini waffle cones. Each waffle cone is 3 inches high and has a radius of inch. What is the volume of a waffle cone?
Answer:
Radius = \(\frac{3}{4}\) in
Radius r = 0.75 in
Height = 3 in
Volume of each waffle cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (0.75)² × 3
Volume = 1.76625 in³
Volume ≈ 1.8 in³

Question 13.
A snack bar sells popcorn ¡n cone-shaped containers. One container has a diameter of 8 inches and a height of 10 inches. How many cubic inches of popcorn does the container hold?
Answer:
Diameter of base = 8 in
Radius = \(\frac{8}{2}\) in
Radius r = 4 in
Height = 10 in
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (4)² × 10
Volume = 167.466 in³
Volume ≈ 167.5 in³

Question 14.
A volcanic cone has a diameter of 300 meters and a height of 150 meters. What is the volume of the cone?
Answer:
Diameter of a volcanic cone = 300 m
Radius = \(\frac{300}{2}\) = 150 m
Height = 150 m
Volume of cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (150)² × 150
Volume = 3532500 m³
Volume of a volcanic cone = 3532500 m³

Question 15.
Multistep Orange traffic cones come in a variety of sizes. Approximate the volume, in cubic inches, of a traffic cone that has a height of 2 feet and a diameter of 10 inches. Use 3.14 for π.
Answer:
Diameter of a traffic cone = 10 in
Radius = \(\frac{10}{2}\) = 5 in
Height = 2 ft
1 foot is equal to 12 inches, so 2 ft = 2 ∙ 12 = 24 in
Volume of the traffic cone = \(\frac{1}{3}\)πr²h
Volume = \(\frac{1}{3}\) × 3.14 × (5)² × 24
Volume = 628 in³
Volume of the traffic cone = 628 in³

Find the missing measure for each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 16.
radius= _________
height = 6 in.
volume = 100.48 in³
Answer:
Let radius be R.
Height = 6 in
Volume = 100.4 in³
Volume of cone = \(\frac{1}{3}\)πr²h
V = \(\frac{1}{3}\)πr²h
So, we have
\(\sqrt{\frac{3 V}{h \pi}}\) = R
\(\sqrt{\frac{3 \times 100.48}{6 \times 3.14}}\) = R
\(\sqrt{\frac{301.44}{18.84}}\) = R
R = \(\sqrt{16}\)
R = 4 in

Question 17.
diameter = 6cm
height = ____________
volume = 56.52 cm³
Answer:
Let height be h
Diameter 6 cm
Radius = \(\frac{6}{2}\) cm
Radius 3 cm
Volume = 56.52 cm³
Volume of cone = \(\frac{1}{3}\)πr²h
V = \(\frac{1}{3}\)πr²h
So, we have
\(\frac{3 V}{r^{2} \pi}\) = h
\(\frac{3 \times 56.52}{3^{2} \times 3.14}\) = h
\(\frac{169.56}{28.26}\) = h
h = 6 cm

Question 18.
The diameter of a cone-shaped container is 4 inches, and its height Is 6 inches. How much greater is the volume of a cylinder shaped container with the same diameter and height? Round your answer to the nearest hundredth. Use 3.14 for π.
Answer:
The diameter of a cone, d = 4 inch
radius of a cone, r = \(\frac{d}{2}\) = \(\frac{4}{2}\) = 2 inches
height of a cone, h = 6 inches
So, Volume of a cone, V_cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × 3.14 × (2)² × 6
= 25.12 in³
And, volume of a cylinder with same diameter and height, V_cylinder
V = πr²h = 3.14 × (2)² × 6
= 75.36 in³
The volume of the cylinder is 50.24 in³ greater than the volume of cone.
The volume of the cylinder is three times the volume of cone.

H.O.T. Focus on Higher Order Thinking

Question 19.
Alex wants to know the volume of sand in an hourglass. When all the sand is in the bottom, he stands a ruler up beside the hourglass and estimates the height of the cone of sand.

a. What else does he need to measure to find the volume of sand?
Answer:
To find the voLume of the sand, he also needs to measure the radius of the base of the hourglass.

b. Make a Conjecture If the volume of sand is increasing at a constant rate, is the height increasing at a constant rate? Explain.
Answer:
The volume of the cone is linearly proportional to the height of the cone. Therefore, if the volume is increasing at a constant rate, the height is also increasing at a constant rate.

Question 20.
Problem Solving The diameter of a cone is x cm, the height is 18 cm, and the volume is 301.44 cm³. What is x? Use 3.14 for π.
Answer:

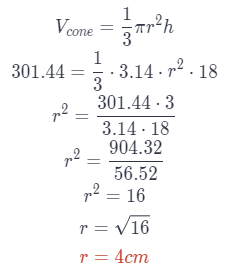
We know that the diameter of the circle is twice its radius, therefore
x = 2 ∙ r
x = 2 ∙ 4
x = 8 cm

Question 21.
Analyze Relationships A cone has a radius of 1 foot and a height of 2 feet. How many cones of liquid would it take to fill a cylinder with a diameter of 2 feet and a height of 2 feet? Explain.
Answer:
The diameter of the base of the cylinder is 2 feet, which means that its radius is 1 foot Its height is 2 feet. The volume of this cylinder is:
V_cylinder = πr²h
V_cylinder = 3.14 ∙ 1² ∙ 2
V_cylinder = 6.28
The radius of the base of the cone is 1 foot and the height of the cone is 2 feet The volume of the cone is:
V_cone = \(\frac{1}{3}\)πr²h
V_cone = \(\frac{1}{3}\) ∙ 3.14 ∙ 1² ∙ 2
V_cone = \(\frac{1}{3}\) ∙ 628
V_cone = \(\frac{1}{3}\) ∙ V_cylinder
V_cone ≈ 2.09
It would take 3 cones of liquid to fill the cylinder.

Question 22.
Critique Reasoning Herb knows that the volume of a cone is one third that of a cylinder with the same base and height. He reasons that a cone with the same height as a given cylinder but 3 times the radius should therefore have the same volume as the cylinder, since \(\frac{1}{3}\) ∙ 3 = 1. Is Herb correct? Explain.
Answer:
The volume of the given cylinder is:
V_cylinder = πr²h
The volume of the cone with the same height h as a given cyLinder but 3 times the radius r is:
V_cone = \(\frac{1}{3}\)π(3r)²h
V_cone = 3πr²h
V_cone = 3V_cylinder
As we can see, Herb is not correct. The volume of the cone is not equal to the volume of the cylinder, but it is three times the volume of the cylinder.