Texas Go Math Grade 8 Lesson 3.4 Answer Key Direct Variation

by

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 3.4 Answer Key Direct Variation.

Texas Go Math Grade 8 Lesson 3.4 Answer Key Direct Variation

Essential Question
How can you solve problems involving direct variation?

Your Turn

Question 1.
The table shows the widths and lengths of United States flags. Determine whether the data set shows direct variation. If so, write an equation that describes the relationship.
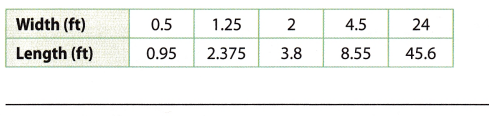
Texas Go Math Grade 8 Lesson 3.4 Answer Key 1
Answer:

Reflect

Question 2.
Does the equation y = \(\frac{3}{2}\)x – 5 show a direct variation? Why or why not?
Answer:

Your Turn

Question 3.
One brand of motorcycle uses an oil-to-gasoline ratio as shown in the graph. The amount of oil that should be added varies directly with the amount of gasoline. Write a direct variation equation that describes the relationship. Use your equation to determine the amount of oil that should be added to 6.5 gallons of gasoline.
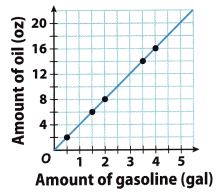
Texas Go Math Grade 8 Lesson 3.4 Answer Key 2
Answer:

Texas Go Math Grade 8 Lesson 3.4 Guided Practice Answer Key 

Determine whether the data sets show direct variation. If so, write an equation that describes the relationship. (Example 1)

Question 1.
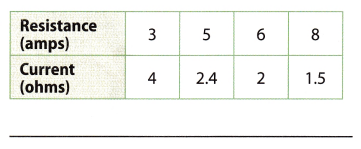
Texas Go Math Grade 8 Lesson 3.4 Answer Key 3
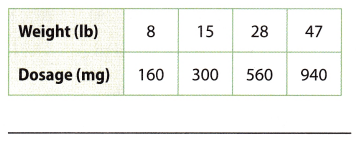
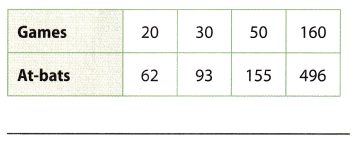
Answer:

Question 2.
Texas Go Math Grade 8 Lesson 3.4 Answer Key 4
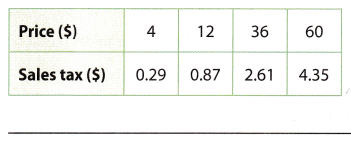
Answer:

Question 3.
Texas Go Math Grade 8 Lesson 3.4 Answer Key 5
Answer:

Question 4.
Texas Go Math Grade 8 Lesson 3.4 Answer Key 6
Answer:

Question 5.
The number of cups in a measure varies directly as the number of tablespoons. Write a direct variation equation that describes the relationship. Use your equation to determine the number of cups in 56 tablespoons. (Example 2)
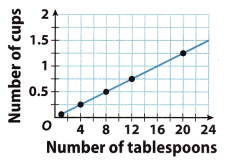
Texas Go Math Grade 8 Lesson 3.4 Answer Key 7
Answer:

Question 6.
The number of calories varies directly with the number of grams of protein. Write a direct variation equation that describes the relationship. Use your equation to determine the number of calories from 25 grams of protein. (Example 2)
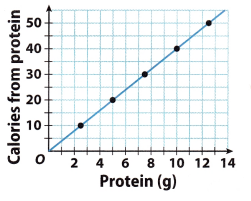
Texas Go Math Grade 8 Lesson 3.4 Answer Key 8
Answer:

Essential Question Check-In

Question 7.
How can you solve problems involving direct variation?
Answer:

Texas Go Math Grade 8 Lesson 3.4 Independent Practice Answer Key 

Question 8.
Vocabulary A _______ is a relationship that can written be as y = kx, where k is a ____.
Answer:

Question 9.
Which equation does NOT represent a direct variation?
(A) y = \(\frac{1}{4}\)
(B) y = -4x
(C) y = 5x + 1
(D) y = 6x
Answer:

Question 10.
Environment Mischa bought an energy-efficient washing machine. The amount of water she saves per wash load compared to her old washer is shown in the table.
Texas Go Math Grade 8 Lesson 3.4 Answer Key 9

a. Determine whether the relationship is a direct variation. If so, write an equation that describes the relationship.
Answer:

b. How much water will she save when washing 8 loads?
Answer:

Question 11.
Sandy wants to build a square garden. Complete the table for the different side lengths.
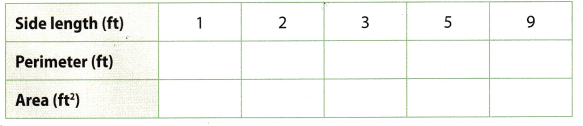
Texas Go Math Grade 8 Lesson 3.4 Answer Key 10

a. Does the perimeter of a square vary directly with the side length? If so, write an equation that describes the relationship. Explain your answer.
Answer:

b. Does the area of a square vary directly with the side length? Why or why not?
Answer:

c. Sandy decides to build her garden with a side length of 3 feet. The border she buys for the perimeter costs $1.99 for a 1.5 foot piece. The soil she buys covers an area of 3 square feet and costs $4.99 a bag. How much does Sandy spend on border and soil for her garden? Explain.
Answer:

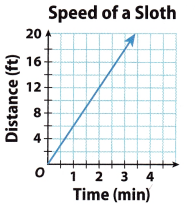
Question 12.
The three-toed sloth is an extremely slow animal. Use the graph to write a direct variation equation for the distance y a sloth will travel in x minutes. How long will it take the sloth to travel 24 feet?
Texas Go Math Grade 8 Lesson 3.4 Answer Key 11
Answer:

Texas Go Math Grade 8 Lesson 3.4 H.O.T. Focus On Higher Order Thinking Answer Key

Question 13.
Critique Reasoning Martin is told that a graph includes the points (2, 5) and (4, 10). He says that this is the graph of the direct variation y = 2.5x. Do you agree? Explain.
Answer:

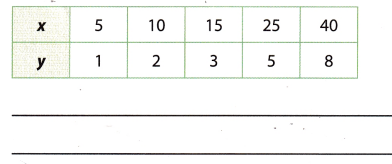
Question 14.
Make a Conjecture If you can write a direct variation equation that relates y to x,y = kx, then you can write a direct variation equation that relates x to y, x = k1y. Make a conjecture about how the constants of variation are related. Use the table to help you decide.
Texas Go Math Grade 8 Lesson 3.4 Answer Key 12
Answer:

Question 15.
Analyze Relationships One graph of a direct variation equation goes through a point A in Quadrant I that is not at the origin. A second graph of a different direct variation equation goes through a point that is one unit to the right of A. Which direct variation equation has a greater constant of variation? Explain.
Answer:

Leave a Comment