Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 2.1 Answer Key Scientific Notation with Positive Powers of 10.
Texas Go Math Grade 8 Lesson 2.1 Answer Key Scientific Notation with Positive Powers of 10
Essential Question
How can you use scientific notation to express very large quantities?
Using Scientific Notation
Scientific notation is a method of expressing very large and very small numbers as a product of a number greater than or equal to 1 and less than 10, and a power of 10.
The weights of various sea creatures are shown in the table. Write the weight of the blue whale in scientific notation.


A. Move the decimal point in 250,000 to the left as many places as necessary to find a number that is greater than or equal to 1 and less than 10.
What number did you find? ____
B. Divide 250,000 by your answer to A . Write your answer as a power of 10.
C. Combine your answers to
A and B to represent 250,000. 
Repeat steps A through C towrite the weight of the whale shark in scientific notation. 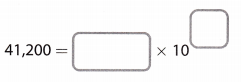
Reflect
Question 1.
How many places to the left did you move the decimal point to write 41,200 in scientific notation? ___________________________________
Answer:
We need to move the decimal point 4 places to the left to write 42,200 in scientific notation.
41,200 = 41,200.0 = 4.1200 × 104 = 4.12 × 104
Four places to the left.
Question 2.
What is the exponent on 10 when you write 41,200 in scientific notation?
Answer:
To write 41,200 in scientific notation, we move the decimal point 4 places to the right and we multiply by 104.
41,200 = 4.12 • 104
4 places to the left
Your Turn
Write each number in scientific notation.
Question 3.
6,400
Answer:
6,400 Given
6.400 Move the decimal point 3 places to the left.
6.4 Remove extra zeros
1000 Divide the original number by the result from above
103 Write the answer as power of 10.
6 × 103 Write the product of the results from above
6 × 103
Question 4.
570,000,000,000
Answer:
570,000,000,000 Given
5.70000000000 Move the decimal point $. Remove extra zeros.
100, 000, 000, 000 Divide the original number by the result from above.
1011 Write the answer as power of 10.
5.7 × 1011 Write the product of the results from above
5.7 × 1011
Question 5.
A light-year is the distance that light travels in a year and is equivalent to 9,461,000,000,000 km. Write this distance in scientific notation.
Answer:
9,461,000, 000,000 Given
9,461000000000 Move the decimal point 11 places to the left.
9.461 Remove extra zeros.
1, 000, 000, 000, 000 Divide the original number by the result from above.
1012 Write the answer as power of 10.
9.461 × 1012 km Write the product of the results from above
9.461 × 1012 km
Question 6.
3.5 × 106 means that decimal should be moved 6 decimals. Placeholders zeros. are added as necessary. Moving one decimal, gives 35 and the remaining five decimals are represented by placeholder zeros.
Question 7.
To express a number in scientific notation we follow some steps:
- We move the decimal point until we get a number that is greater than or equal to 1 and less than 10.
- We divide the original number with the one we got from Step 1.
- We write the product of the results from Step I and Step 2.
In our case. the given number is already greater than 1 and less than 10. So it can be written as:
5.3 = 5.3 100
The exponent on 10 is 0.
The exponent on 10 is 0
Question 8.
7.034 × 109 Given
9 places Use exponent of the power of 10 to determine the number places to move the decimal point
7,034 000000 Place the decimal point Since you are going to write a number greater than 7.035, move decimal point to the right. Add placeholder zeros if necessary. The number
7.034 × 109 in standard form is 7, 034,000,000
Question 9.
2.36 × 105 Given
5 places Use exponent of the power of 10 to determine the number places to move the decimal point
236,000 Place the decimal point Since you are going to write a number greater than 2.36, move decimal point to the right Add placeholder zeros if necessary.
The number 2.36 × 105 in standard form is 236,000
Question 10.
5 × 106 Given
6 places Use exponent of the power of 10 to determine the number places to move the decimal point
5, 000, 000 Place the decimal point Since you are going to write a number greater than 5, move decimal point to the right. Add placeholder zeros if necessary.
The number 5 × 106 grams in standard form is 5, 000, 000 grams
Texas Go Math Grade 8 Lesson 2.1 Guided Practice Answer Key
Question 1.
58,927 Given
5.8927 Move the decimal point 4 places to the Left.
10,000 Divide the original number by the result from above.
104 Write the answer as power of 10.
5.8927 × 104 Write the product of the results from above
5.8927 × 104
Question 2.
1, 304, 000,000 Given
1.304000000 Move me decimal point 9 places to the left.
1.304 Remove extra zeros.
1,000,000 Divide the original number by the result from above.
109 Write the answer as power of 10.
1.304 × 109 Write the product of the results from above
1.304 × 109
Question 3.
6,730,000 Given
6.730000 Move the decimal point 6 places to the left.
6.73 Remove extra zeros.
1,000,000 Divide the original number by the result from above.
106 Write the answer as power of 10.
6.73 × 106 Write the product of the results from above
6.73 × 106
Question 4.
13 300 Given (1)
1.3300 Move the decimal point L places to the left (2)
1.33 Remove extra zeroes (3)
10000 = 104 Divide the original number by 1.33 (4)
1.33 × 104 Multiply numbers from above
1.33 × 104
Question 5.
97, 700, 000, 000, 000, 000, 000, 000 Given
9.7700000000000000000000 Move the decimal point 22 places to the left
9.77 Remove extra zeros.
10,000, 000,000,000, 000,000,000 Divide the original number by the result from above.
1022 Write the answer as power of 10.
9.77 × 1022 Write the product of the results from above
Question 6.
384,000 Given
3.84000 Move the decimal point 5 places to the left
3.84 Remove extra zeros.
100,000 Divide the original number by the result from above.
105 Write the answer as power of 10.
3.84 × 105 Write the product of the results from above
3.84 × 105
Question 7.
4 × 105 Given
5 places Use exponent of the power of 10 to determine the number places to move the decimal point
400,000 Place the decimal point Since you are going to write a number greater than 4, move decimal point to the right. Add placeholder zeros if necessary.
The number 4 × 105 in standard form is 400, 000
Question 8.
1.8499 × 109 Given
9 places use exponent of the power of 10 to determine the number places to move the decimal point
1,849,900,000 Place the decimal point Since you are going to write a number greater than 1.8499, move decimal point to the right. Add placeholder zeros if necessary.
The number 1.8499 × 109 in standard form is 1, 849, 900, 000
Question 9.
6.41 × 103 Given
3 places use exponent of the power of 10 to determine the number places to move the decimal point
6,410 Place the decimal point Since you are going to write a number greater than 6.41, move decimal point to the right. Add placeholder zeros if necessary.
The number 6.41 × 103 in standard form is 6, 410
Question 10.
8.456 × 107 Given
7 places use exponent of the power of 10 to determine the number places to move the decimal point
84, 560, 000 Place the decimal point Since you are going to write a number greater than 8.456, move decimal point to the right. Add placeholder zeros if necessary.
The number
8.456 × 107 in standard form is 84, 560, 000
Question 11.
8 × 105 Given
5 places use exponent of the power of 10 to determine the number places to move the decimal point
800,000 Place the decimal point Since you are going to write a number greater than 8, move decimal point to the right. Add placeholder zeros if necessary.
The number
8 × 105 in standard form is 800, 000
Question 12.
9 × 1010 Given
10 places use exponent of the power of 10 to determine the number places to move the decimal point
90, 000, 000, 000 Place the decimal point Since you are going to write a number greater than 8, move decimal point to the right. Add placeholder zeros if necessary.
The number 9 × 1010 in standard form is 90, 000, 000, 000
Question 13.
5.4 × 104 Given
4 places use exponent of the power of 10 to determine the number places to move the decimal point
54, 000 Place the decimal point Since you are going to write a number greater than 5.4, move decimal point to the right. Add placeholder zeros if necessary.
The time in standard form is 54, 000 seconds
Question 14.
7.6 × 106 Given
6 places use exponent of the power of 10 to determine the number places to move the decimal point
7, 600, 000 Place the decimal point Since you are going to write a number greater than 7.6, move decimal point to the right. Add placeholder zeros if necessary.
The time in standard form is 7, 600, 000 cans
Question 15.
3,482,000.000 Given (1)
3.482000000 Move the decimal point 9 places to the left. (2)
3.482 Remove extra zeroes (3)
1000000000 = 109 Divide the original number by 3.482 (4)
3.482 × 109 Multiply numbers from steps (3) and (4) (5)
Rewrite the number as a decimal that has a whole between 1 and 10 (not including 10) multiplied by 109 where 9 is the number of places you moved the decimal. Click for details!
Texas Go Math Grade 8 Lesson 2.1 Independent Practice Answer Key
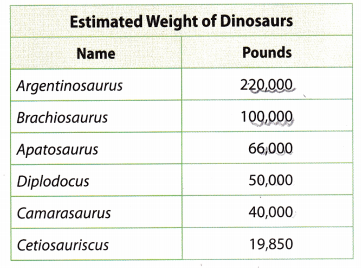
Paleontology Use the table for problems 16-21. Write the estimated weight of each dinosaur in scientific notation.
Question 16.
Apatosaurus
Answer:

6.6 × 104
Question 17.
Argentinosaurus _____
Answer:
The weight of Argentinosaurus is 220, 000 pounds. Write that number in a scientific notation.

2.2 × 105
Question 18.
Brachiosaurus _____
Answer:
The weight of Brachiosaurus is 100, 000 pounds. Write that number in a scientific notation.

1 × 105
Question 19.
Camarasaurus ____
Answer:
The weight of Camarasaurus is 40, 000 pounds. Write that number in a scientific notation.

4 × 104
Question 20.
Ceriosauriscus ________________________
Answer:
Estimated weight of Cetiosauriscus is 19,850 pounds. To express this number in scientific notation:
Move the decimal point 4 places to the left, so we get a number that is greater than or equal to 1 and less
than 10. We remove the extra zeros.
1.9800 = 1.98
Divide the original number by the result from above. Write the answer as a power of 10.
\(\frac{19,800}{1.98}\) = 10,000 = 104
Write the product of the results from above.
19,800 = 1.98 • 104
Question 21.
Diplodocus _____________________
Answer:
The weight of Diplodocus is 50,000 pounds. Write that number in a scientific notation.

5 × 104
Question 22.
A single little brown bat can eat up to 1000 mosquitoes in a single hour. Express in scientific notation how many
mosquitoes a little brown bat might eat in 10.5 hours.
Answer:
Since a Little brown bat can eat up to 1, 000 mosquitoes in an hour it can eat 10.5 times more in 10.5 hours, SO:
10.5 × 1,000 = 10,500
Write 10, 500 in a scientific notation.

1.05 × 104
Question 23.
Multistep Samuel can type nearly 40 words per minute. Use this information to find the number of hours it would take him to type 2.6 × 105 words.
Answer:
To find the member of hours N, we need to divide the total number of words by typing speed (words per minute). We have:
N = \(\frac{2.6 \cdot 10^{5}}{40}\)
To simplify, we write 40 in a scientific form as 4 • 101:
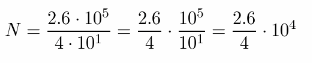
To write \(\frac{2.6}{4}\) as a decimal, we divide the numerator by the denominator until the remainder is zero or until the digits in the quotient begin to repeat.
We add as many zeros after the decimal point in the dividend as needed.
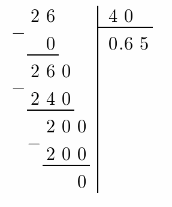
Therefore,
N = 0.65 . 104
N = 0.65 . 103 minutes
To convert from minutes to hours, we divide the result by 60:
N = \(\frac{6.5 \cdot 10^{3}}{60}\)
To simplify, we write 60 in a scientific form as 6 . 101:
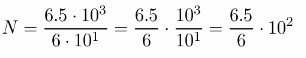
To write \(\frac{6.5}{6}\) as a decimal, we divide the numerator by the denominator until the remainder is zero or until the digits in the quotient begin to repeat.
We add as many zeros after the decimal point in the dividend as needed.

108.3 hours = 108 hours 20 minutes
Question 24.
Entomology A tropical species of mite named Archegozetes longisetosus is the record holder for the strongest insect in the world. It can lift up to 1.182 × 103 times its own weight.
a. If you were as strong as this insect, explain how you could find how many pounds you could lift.
Answer:
Number of pounds you can lift by multiplying 1.182 × 103 by your weight.
Since you are as strong as the ant which can lift up to 1.182 × 103 its own weight.
b. Complete the calculation to find how much you could lift, in pounds, if you were as strong as an Archegozetes longisetosus mite. Express your answer in both scientific notation and standard notation.
Answer:
Number of pounds = 100 * 1.182 × 103 Let weight = 100 pounds
102 * 1.182 × 103, Simplify
1.182 × 105 In scientific notation. Add the exponent of 10
118200 In standard notation. Move the decimal 5 places to the right. Add placeholder zeros if necessary.
Question 25.
During a discussion in science class, Sharon learns that at birth an elephant weighs around 230 pounds. In four herds of elephants tracked by conservationists, about 20 calves were born during the summer. In scientific notation, express approximately how much the calves weighed all together.
Answer:
Total weight of calves = 230 * 20 = 4600 where each elephant calves weight 230 pounds and 20 calves are born
4.600 Move the decimal point 4 places to the left
Remove extra zeros.
1, 000 Divide the original number by the result from above
103 Write the answer as power of 10.
4.6 × 103 Write the product of the results from above
The total weight is $4.6 \times
10^{3}$ pounds
4.6 × 103 pounds
Question 26.
Classifying Numbers Which of the following numbers are written in scientific notation?
0.641 × 103 9.999 × 104
2 × 101 4.38 × 510
Answer:
In order for a number to be written in scientific notation they must be of the format
c × 103
where c is a decimal number greater or equal to 1 and less than 10 and n is an integer, lets name that rule: Rule (1).
Using this rule we have to check which numbers are written in scientific notation:
0.641 × 103 Not in scientific notation, correct woud be 641 × 102
9.999 × 104 This is in scientific notation according to Rule (1)
2 × 101 This is in scientific notation according to Rule (1).
4.38 × 510 Not in scientific notation because it is not in a correct form according to Rule (1)
9.999 × 104 and 2 × 101 are written in scientific notation.
Question 27.
Explain the Error Polly’s parents’ car weighs about 3500 pounds. Samantha, Esther, and Polly each wrote the weight of the car in scientific notation. Polly wrote 35.0 × 102, Samantha wrote 0.35 × 104, and Esther wrote 3.5 × 104.
a. Which of these girls, if any, is correct?
Answer:
3500 pounds Given
None of the girls is correct Correct scientific notation: 3.5 × 103
b. Explain the mistakes of those who got the question wrong.
Answer:
Potty did not express the number such first part is greater than or equal to 1 and less than 10
Scientific notation is a way of expressing numbers as a product of number greater than or equal to 1 and
less than 10 and 10
Samantha did not express the number such first part is greater than or equal to $1$ and less than $10$ Esther did not express the exponent of $10$ correctly
Question 28.
Justify Reasoning If you were a biologist counting very large numbers of cells as part of your research, give several reasons why you might prefer to record your cell counts in scientific notation instead of standard notation.
Answer:
Reason 1
It is a standard way of writing resuLts in a scientific environment accepted and used by scientists all over the world.
Reason 2
It is easier to compare large numbers since you only have to compare the exponents on the power 10n or if they are the same number between 1 and 10 that are multiplied by 10’
Reason 3
It is much easier to write very large (or very small) numbers and take less space, for example:
15, 000, 000. 000, 000, 000, 000 = 1.5 × 1019
1) It is a notation accepted around the world and used in science.
2) It is easy to compare numbers.
3) It is easier to write large numbers.
Texas Go Math Grade 8 Lesson 2.1 H.O.T. Focus On Higher Order Thinking Answer Key
Question 29.
Draw Conclusions Which measurement would be least likely to be written in scientific notation: number of stars in a galaxy, number of grains of sand on a beach, speed of a car, or population of a country? Explain your reasoning.
Answer:
Scientific notation is used to express measurements that are extremely large or extremely small. Number of stars in a galaxy and number of grains of sand on a beach are extremely large, so we use scientific notation for those. Comparing speed of a car and population of a country, it is clear that the speed of a car is a smaller number. Therefore, the speed of a car is less likely to be written in scientific notation.
The speed of a car is less likely to be written in scientific notation.
Question 30.
Analyze Relationships Compare the two numbers to find which is greater. Explain how you can compare them without writing them in standard notation first.
4.5 × 106 2.1 × 108
Answer:
We can easily compare them by just comparing the exponents of the power 10n. In this case we have 106 and 108, since 108 > 106 every number greater or equal to 1 and less than 10 multiplied by 106 is smaller than any number greater or equal to 1 and less than 10 multiplied by 108
We can conclude: 4.5 × 106 < 2.1 × 108
Comparing the exponents we have: 4.5 × 106 < 2.1 × 108
Question 31.
Communicate Mathematical Ideas To determine whether a number is written in scientific notation, what test can you apply to the first factor, and what test can you apply to the second factor?
Answer:
Scientific notation is in the form of: c × 10n so c is the first factor and 10n is the second factor.
To the first factor we can apply the test: if it is a decimal number greater than or equal to 1 but less than 10 it can
be a first factor in a scientific notation.
To the second factor we can apply the test: if its a power of 10 it can be a second factor in a scientific notation.
First factor has to be greater or equal to 1 and less than 10.
Second factor must be a power of 10.