Texas Go Math Grade 7 Unit 4 Study Guide Review Answer Key

Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Unit 4 Study Guide Review Answer Key.

Texas Go Math Grade 7 Unit 4 Study Guide Review Answer Key

Linear Relationships

Essential Question
How can you use linear relationships to solve real-world problems?

Example
Ross earns a set rate of $10 for babysitting, plus $6 per hour. Represent the relationship using a table, an equation, and a graph of the linear relationship.


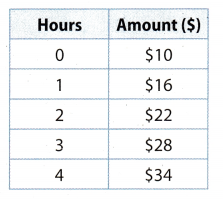
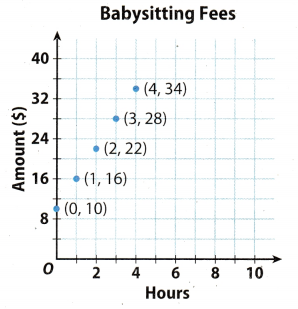
Write an equation for the amount y in dollars earned for x hours.
Amount = $10 + $6 per hour .
y = 10 + 6x

Texas Go Math Grade 7 Unit 4 Exercises Answer Key

Question 1.
The cost of a box of cupcakes is $1.50 per cupcake plus $3. Complete the table to represent the linear relationship. (Lesson 7.1)

Answer:

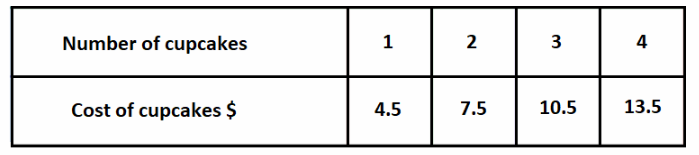
Box of cupcake + 1 cupcake = 1.5 + 1 . 3 = 4.5
Box of cupcake + 2 cupcake = 1.5 + 2 . 3 = 7.5
Box of cupcake + 3 cupcake = 1.5 + 3 . 3 = 10.5
Box of cupcake + 4 cupcake= 1.5 + 4 . 3 = 13.5

y = Box of cupcake + x cupcake

Question 2.
The score a student receives on a standardized test is based on the number of correct answers, as shown in the table. Use the table to give a verbal description of the relationship between correct answers and score. (Lesson 7.1)

Answer:
The relationship between the correct answers and score is:
The score is 200 plus an additional of the correct answer multiplied by 2.

Question 3.
Steve is saving for his daughter’s college education. He opens an account with $2,400 and deposits $40 per month. Represent the relationship using a table and an equation. (Lesson 7.2)
Answer:

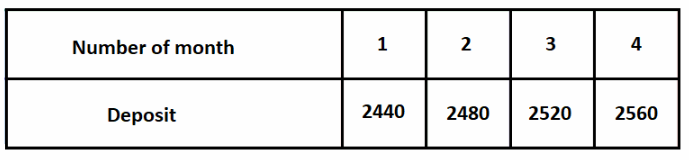
y = 2400 + 40x
1 month
y = 2400 + 40 . 1 = 2440
2 months
y = 2400 + 40 . 2 = 2480
3 months
y = 2400 + 40 . 3 = 2520
4 months
y = 2400 + 40 . 4 = 2560

y = 2400 + 40x

Question 4.
Tonya has a 2-page story she wants to expand. She plans to write 3 pages per day until it is done. Represent the relationship using a table, an equation, and a graph. (Les5on 7.2)

Answer:

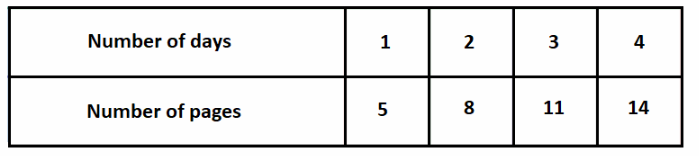
y = 2 + 3x
1 day
y = 2 + 3 . 1 = 5
2 days
y = 2 + 3 . 2 = 8
3 days
y = 2 + 3 . 3 = 11
4 days
y = 2 + 3 . 4 = 14

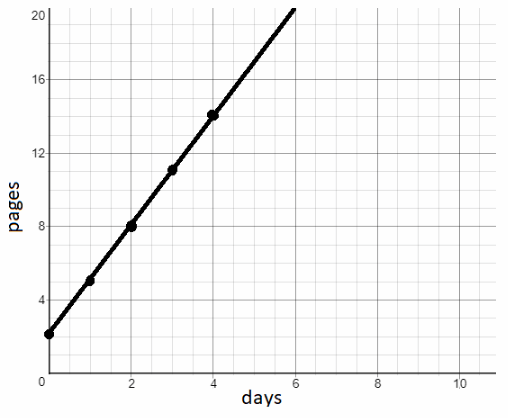
y = 2 + 3x

Equations and Inequalities

Essential Question
How can you use equations and inequalities to solve real-world problems?

Example 1
A clothing store sells clothing for 2 times the wholesale cost plus $10. The store sells a pair of pants for $48. How much did the store pay for the pants? Represent the solution on a number line.
Let w represent the wholesale cost of the pants, or the price paid by the store.

The store paid $19 for the pants.

Example 2
Determine which, if any, of these values makes the inequality
-7x + 42 ≤ 28 true: x = -1, x = 2, x = 5.

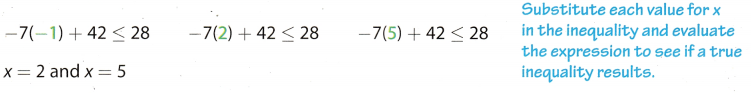
Texas Go Math Grade 7 Unit 4 Exercises Answer Key

Question 1.
The cost of a ticket to an amusement park is $42 per person. For groups of up to 8 people, the cost per ticket decreases by $3 for each person in the group. Marcos’s ticket cost $30. Write and solve an equation to find the number of people in Marcos’s group. (Lessons 8.1, 8.2)
Answer:
Assign a variable for the unknown value. Let x be the number of people in Marco’s group. The equation for the
given problem is:
42 – 3x = 30
Determine the number of people in Marco’s group.
42 – 3x = 30 Write the equation
42 – 3x – 42 = 30 – 42 Subtract 42 from both sides
-3x = -12 Simplify
\(\frac{-3 x}{-3}\) = \(\frac{-12}{-3}\) Divide both sides by -3
x = 4 Simplify
There are 4 people in Marco’s group.

Solve each equation. Graph the solution on a number line. (Lesson 8.2)

Question 2.
8x – 28 = 44

Answer:
Add 28 to both sides.
8x – 28 + 28 = 44 + 28
8x = 72 Divide both sides by 8.


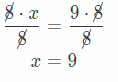
x = 9

Question 3.
-5z + 4 = 34

Answer:
Subtract 4 from both sides.
– 5z + 4 – 4 = 34 – 4
– 5z = 30 Divide both sides by (-5).


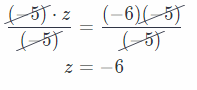
z = -6

Question 4.
Prudie needs $90 or more to be able to take her family out to dinner. She has already saved $30 and wants to take her family out to eat in 4 days. (Lesson 6.3)

a. Suppose that Prudie saves the same each day. Write an inequality to find how much she needs to save each day.
Answer:
a) Sum $30 Prudie already has and 1x, where r represent how much money
she needs to save each day to raise at least $90.
$30 + 4r ≥ 890 Subtract $30 from both sides.
-$30 + $30 + 4x ≥ -$30 + $90
4x ≥ $60 Divide both sides by 4.

x ≥ $15

b. Suppose that Prudie saves $18 each day. Will she have enough money to take her family to dinner in 4 days? Explain.
Answer:
Yes she will, because $18 satisfies the inequation. Lets check.

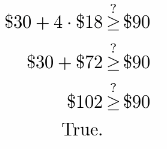
x ≥ $15

Solve each inequality. Graph and check the solution. (Lesson 8.4)

Question 5.
15 + 5y > 45

Answer:
Subtract 15 from both sides
-15 + 15 + 5y > – 15 + 45
5y > 30 Divide both sides by .

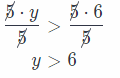
Check the solution for y > 6. For example, y = 7.

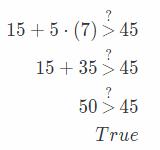
This inequality is shown in the picture.

y > 6

Question 6.
7x – 2 ≤ 61

Answer:
Add 2 to both sides
7x – 2 + 2 ≤ 61 + 2
7x ≤ 63 Divide both sides by 7.

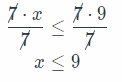
Check the solution for x ≤ 9. For example, x = 8.

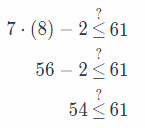
True
This inequality is shown in the picture.

x ≤ 9

Texas Go Math Grade 7 Unit 4 Performance Tasks Answer Key

Question 1.
Careers in Math Mechanical Engineer A mechanical engineer is testing the amount of force needed to make a spring stretch by a given amount. The force y is measured in units called Newtons, abbreviated N. The stretch x is measured in centimeters. Her results are shown in the graph.

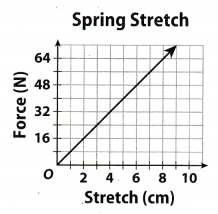
a. Write an equation for the line. Explain, using the graph and then using the equation, why the relationship is proportional.
Answer:
Based on the graph, use (2, 16). This point represents the force (16 N) with a stretch (2 cm). Using this point,
determine the value of k in k = \(\frac{y}{x}\).
k = \(\frac{y}{x}\) = \(\frac{16}{2}\) = 8
Substitute the value of k in the given form y = kx. The equation for the given graph 5:
y = 8x
The graph is said to be proportional because the graph is a straight line through the origin. Furthermore, the rate
of change is constant.

b. Identify the rate of change and the constant of proportionality.
Answer:
Based on the equation y = 8x, the rate of change and constant of proportionality is 8. This is because the comparison between the force and stretch in the given graph is constant for every point on the Line.

c. What is the meaning of the constant of proportionality in the context of the problem?
Answer:
The constant of proportionality in the problem showed that when there is an increase ¡n the stretch of the spring the force also increases by 8.

Question 2.
A math tutor charges $30 for a consultation, and then $25 per hour. An online tutoring service charges $30 per hour.

a. Does either service represent a proportional relationship? Explain.
Answer:
The online tutoring service represents a proportion relationship. This is because the relationship between the two
quantities is constant or the ratio of one quantity to the other is constant

b. Write an equation for the cost c of h hours of tutoring for each service. Which service charges less for 4 hours of tutoring? Show your work.
Answer:
The equation for the math tutor is:
30 + 25h = c
The equation for the online tutoring service is:
30h = c
Using the two equations, determine which service will charge less
Math tutor:
30 + 25h = c Write the equation
30 + 25(4) = c Substitute the value
30 + 1oo = c Multiply the values
130 = c Add the values
Online Tutoring
30h = c Write the equation
30(4) = c Substitute the value
120 = c Multiply the values
The online tutoring service will charge less compared to math tutor.

Texas Go Math Grade 7 Unit 4 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
Which description corresponds to the relationship shown in the table?

(A) earning $10 per hour
(B) earning $8 per hour plus $10 in tips
(C) earning $7 per hour plus $15 in tips
(D) earning $8.50 per hour
Answer:
(C) earning $7 per hour plus $15 in tips

Explanation:
y = 15 + 7x
x = number of hours
y = amount of pay
C. earning $7 per hours plus $15 in tips.

Question 2.
Timothy began the week with $35. He bought lunch at school, paying $2.25 for each meal. Let x be the number of meals he bought at school and y be the amount of money he had left at the end of the week. Which equation represents the relationship in the situation?
(A) y = 2.25x + 35
(B) y = 35 – 2.25x
(C) x = 35 – 2.25y
(D) y = 2.25x – 35
Answer:
(B) y = 35 – 2.25x

Explanation:
Timothy has $35 and spend $2.25 for each meal at school, hence amount of money he has decreases for each meal he buys.
y = 35 – 2.25x

Question 3.
Which table represents the linear relationship described by the equation y = 3x + 9?

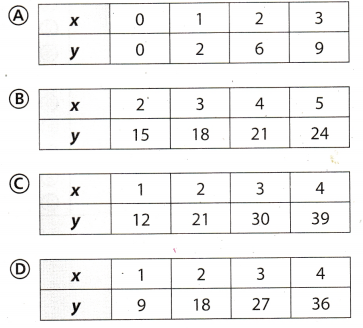
Answer:

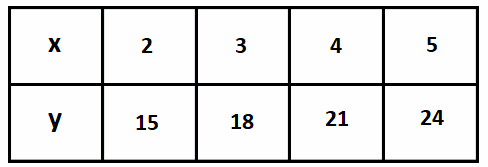
x = 2
y = 3(2) + 9 = 15
x = 3
y = 3(3) + 9 = 18
x = 4
y = 3(4) + 9 = 21
x = 5
y = 3(5) + 9 = 24

y = 3x + 9 = 15

Question 4.
A taxi costs $1.65 for the first mile and $0.85 for each additional mile. Which equation could be solved to find the number x of additional miles traveled in a taxi given that the total cost of the trip is $20?
(A) 1.65x + 0.85 = 20
(B) 0.85x + 1.65 = 20
(C) 1.65x – 0.85 = 20
(D) 0.85x – 1.65 = 20
Answer:
(B) 0.85x + 1.65 = 20

Explanation:
The equation will be:
the cost of the first mile plus number of miles multiplied by the cost of each mile equals to total cost of the trip.
Hence
0.85x + 1.65 = 20

Question 5.
A bag contains 7 purple beads, 4 blue beads, and 7 pink beads. What is the probability of not drawing a blue bead?
(A) \(\frac{4}{18}\)
(B) \(\frac{7}{18}\)
(C) \(\frac{11}{18}\)
(D) \(\frac{14}{18}\)
Answer:
(D) \(\frac{14}{18}\)

Explanation:
Total number of beads in a bag is 18.

The sum of the probabilities of an event and its complement equals 1.
P(event) + P(complement) = 1
P(blue) + P(not blue) = 1
\(\frac{4}{18}\) + P(not blue) = 1 Subtract \(\frac{4}{18}\) from both sides.
P(not blue) = 1 – \(\frac{4}{18}\)
P(not blue) = \(\frac{14}{18}\)
The probability of not drawing a blue bead is \(\frac{14}{18}\).

Question 6.
Which equation has the solution x = 12?
(A) 4x + 3 = 45
(B) 3x + 6 = 42
(C) 2x – 5 = 29
(D) 5x – 8 = 68
Answer:
(B) 3x + 6 = 42

Explanation:
The answer is 3x + 6 = 42
Proof:

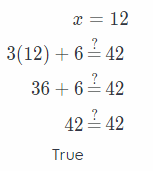
3x + 6 = 42

Question 7.
The 23 members of the school jazz band are trying to raise at least $1,800 to cover the cost of traveling to a competition. The members have already raised $750. Which inequality could you solve to find the amount that each member should raise to meet the goal?
(A) 23x + 750 > 1,800
(B) 23x + 750 ≥ 1,800
(C) 23x + 750 < 1,800
(D) 23x + 750 ≤ 1,800
Answer:
(B) 23x + 750 ≥ 1,800

Explanation:
Sum the amount they already have and number of members multiplied by the amount each member should raise to collect at least $1800.
23x + 750 ≥ 1800

Question 8.
What is the solution of the inequality 2x – 9 < 7?
(A) x < 8 (B) x ≤ 8 (C) x > 8
(D) x ≥ 8
Answer:
Add 9 to both sides.
2x – 9 + 9 < 7 + 9
2x < 16 Divide both sides by 2
\(\frac{2 x}{2}\) < \(\frac{16}{2}\)
x < 8

Question 9.
Carter rolls a fair number cube 18 times. Which is the best prediction for the number of times he will roll a number that is odd and less than 3?
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
(B) 3

Explanation:
Total number of outcome in a fair dice = 6
Number of outcome which is odd and less than 3 = 1
Probability of outcome which is odd and less than 3 = \(\frac{1}{6}\)
But it is given in the problem that dice is rolled for 18 times. So the probability of outcome which is an odd number and Less than 3 will be in the same proportion.
Let the number of rolls which results in an odd number and less than 3 be x.
\(\frac{x}{18}\) = \(\frac{1}{6}\) (By proportion)
x = \(\frac{18}{6}\) (Cross-multiplying)
x = 3 (Simplifying)
So, 3 rolls are expected for result of an odd number and less than 3
Hence, option B is correct answer.

Question 10.
Which inequality has the solution shown?

(A) 3x + 5 < 2
(B) 4x + 12 < 4
(C) 2x + 5 ≤ 1
(D) 3x + 6 ≤ 3
Answer:
(A) 3x + 5 < 2

Explanation:
Subtract 5 from both sides
3x + 5 – 5 < 2 – 5
3x < – 3 Divide both sides by 3.
\(\frac{3 x}{3}\) < \(\frac{-3}{3}\)
x < -1

Gridded Response

Question 11.
What is the greatest whole number value that makes the inequality 4x + 4 ≤ 12 true?

Answer:
Subtract 4 from both sides.
4x + 4 – 4 ≤ 12 – 4
4x ≤ 8 Divide both sides by 4.
\(\frac{4 x}{4}\) ≤ \(\frac{8}{4}\)
x ≤ 2
The number 2 is the greatest whole number that makes the inequality true.

Question 12.
The rectangles shown are similar. The dimensions are given in inches.

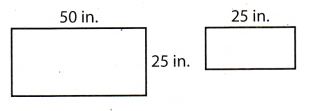
What is the width of the smaller rectangle?

Answer:
The bigger rectangle
l₁ = 50 in.
w₁ = 25 in.
The smaller rectangle
l₂ = 25 in.
w₂ = x in.
Because they are similar, the corresponding length of sides are proportional.

The width of the smaller rectangle is 12.5 in.

Hot Tip!
Gridded responses can be positive or negative numbers. Enter any negative signs in the first column. Check your work!

Question 13.
What is the solution to the equation 8x – 11 = 77?

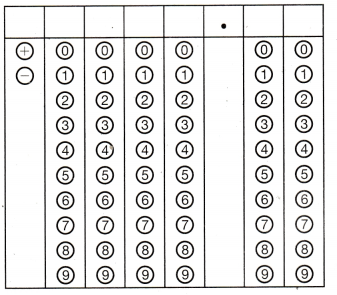
Answer:
Add 11 to both sides.
8x – 11 + 11 = 77 + 11
8x = 88 Divide both sides by 8.

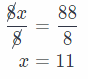
The solution is 11

Vocabulary Preview

Use the puzzle to preview key vocabulary from this unit. Unscramble the circled letters to answer the riddle at the bottom of the page.

As one quantity changes by a constant amount, the other quantity also changes by a constant amount. (Lesson 7.1)

A special type of linear relationship in which the rate of change is constant, or one in which the ratio of one quantity to the other is constant. (Lesson 7.1)

An equation with more than one operation. (Lesson 8.1)

A variable whose value is less than zero. (Lesson 8.1)

A variable whose value is greater than zero. (Lesson 8.1)

Q: Why does the sum of -4 and 3 complain more than the sum of -3 and 5?
A: It’s the ___ ___ ___ __ ___ ___ ___ ___ ___ __ ___ !
Answer: