Texas Go Math Grade 7 Unit 2 Study Guide Review Answer Key

Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Unit 2 Study Guide Review Answer Key.

Texas Go Math Grade 7 Unit 2 Study Guide Review Answer Key

Texas Go Math Grade 7 Unit 2 Exercises Answer Key

Module 2 Rates and Proportionality

Question 1.
Steve uses \(\frac{8}{9}\) gallon of paint to paint 4 identical birdhouses. How many gallons of paint does he use for each birdhouse? (Lesson 2.1)
Answer:
For 4 identical birdhouses Steve uses \(\frac{8}{9}\) gallons of paint.
To find how many gallons he needs for one birdhouse, we have to divide \(\frac{8}{9}\) by 4.
\(\frac{8}{9}\) ÷ 4 = \(\frac{8}{9}\) ∙ \(\frac{1}{4}\) Multiply by the reciprocaL of the divisor
= \(\frac{8 \cdot 1}{9 \cdot 4}\)
= \(\frac{8}{36}\)
= \(\frac{4 \cdot 2}{4 \cdot 9}\)
= \(\frac{2}{9}\)
He uses \(\frac{2}{9}\) gallons of the paint for each birdhouse.

Question 2.
Ron walks 0.5 mile on the track in 10 minutes. Stevie walks 0.25 mile on the track in 6 minutes. Find the unit rate for each walker in miles per hour. Who is the faster walker? (Lesson 2.1)
Answer:
To find how much miles Ron waLks for one minute, divide number of miles by number of minutes.
\(\frac{0.5}{10}\) = 0.05
For one minute he waLks 0.05 miles.
For one hour he walks 0.05 ∙ 60 = 3 miles.
Therefore, he walks 3 miles per hour.
Repeat procedure with Stevie.
\(\frac{0.25}{6}\) = 0.04
For one hour he walks 0.04 ∙ 60 = 2.4 miles.
Therefore, he walks 2.4 miles per hour.
We get 3 > 2.4, therefore, Ron is the faster walker.

Question 3.
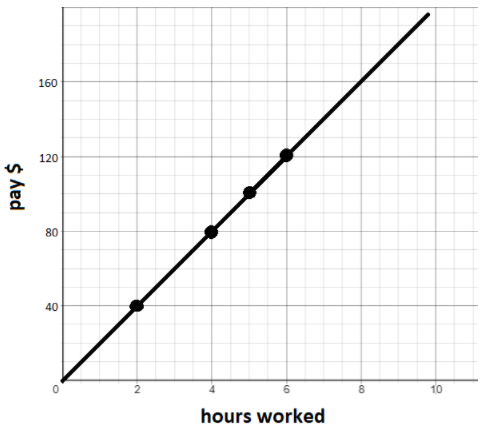
(Lessons 2.2, 2.3) The table below shows the proportional relationship between Juan’s pay and the hours he works. Complete the table. Plot the data and connect the points with a line. (Lessons 2.2, 2.3)

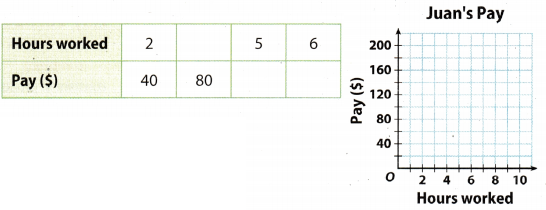
Answer:
First, find the constant of proportionality.
Let y be pay ($) and x be hours worked.
The constant of proportionality = \(\frac{y}{x}\) = \(\frac{40}{2}\) = 20
Hence, for I hour of work he earns $20.
To find how many hours he needs to work for $80. we divide 80 by the constant of proportionality.
\(\frac{80}{20}\) = 4
For 1 hour he earns $20, so for 5 hours he earns 5 ∙ 20 = $100.
For 1 hour he earns $20. so for 6 hours he earns 6 ∙ 20 = $120.

Module 3 Proportions and Percent

Convert each measurement. (Lesson 3.1)

Question 1.
7 centimeters ≈ __________ inches
Answer:
As we know 1 inch ≈ 2.54 centimeters.
Divide both sides by 2.54.
You get:
≈ 1 cm
To calculate for 7 centimeters, multiply both sides by 7.
7 ∙ \(\frac{1 \mathrm{~ in}}{2.54}\) ≈ 7 ∙ 1 cm
7 0.4 in ≈ 7 cm
2.8 in ≈ 7 cm

Question 2.
10 pounds ≈ __________ kilograms
Answer:
1 pound ≈ 0.45 kg
10 pound ≈ 4.5 kg

Question 3.
24 kilometers ≈ ___________ miles
Answer:
As we know 1 mile ≈ 1.61 kilometers
Divide both sides by 1.61.
You get:
\(\frac{1 \mathrm{~ mi}}{1.61}\) ≈ 1 km
To calculate for 24 kilometers. multipLy both sides by 24.
24 ∙ \(\frac{1 \mathrm{~ mi}}{1.61}\) ≈ 24. 1 km
24 ∙ 0.62 mi ≈ 24 km
14.9 mi ≈ 24 km

Question 4.
12 quarts ≈ _____________ liters
Answer:
1 quart ≈ 0.95 l
12 quart ≈ 11.4 l

Question 5.
Michelle purchased 25 audio files in January. In February she purchased 40 audio files. Find the percent increase. (Lesson 3.2)
Answer:
First we find amount of change.
Amount of Change = Purchased audio files in February – Purchased audio files in January
= 40 – 25
= 15
Now, we have all, necessary data to find percent change.

= \(\frac{15}{25}\)
= \(\frac{3}{5}\)
= 0.6 = 60%

Question 6.
Sam’s dog weighs 72 pounds. The vet suggests that for the dog’s health, its weight should decrease by 12.5 . percent. According to the vet, what is a healthy weight for the dog? (Lesson 3.2)
Answer:
Find 12.5 percent od 72 and subtract it from 72
Write percent as fractor.
\(\frac{12.5}{100}\) ∙ 72 = 0.125 ∙ 72 = 9
The healthy weight for the dog is 72 – 9 = 63 pounds.

Question 7.
The original price of a barbecue grill is $79.50. The grill is marked down 15%. What is the sale price of the grill? (Lesson 3.3)
Answer:
Original price is $79.50.
Find 15% percent of original price.
79.50 ∙ \(\frac{15}{100}\) = 79.50 ∙ 0.15 = 11.9
Subtract the result from original price.
79.50 – 11.9 = $67.6
Therefore, the sale price of grill is $67.6.

Question 8.
A sporting goods store marks up the cost s of soccer balls by 250%. Write an expression that represents the retail cost of the soccer balls. The store buys soccer balls for $5.00 each. What is the retail price of the soccer balls? (Lesson 3.3)
Answer:
Store pays $5 for each soccer hail and sells it for 250% of the price she pays for the ball.
Find the 250% of the 5.
Write percent as a fraction.
\(\frac{250}{100}\) ∙ 5 = 2.55
= 12.5
The retail price of the soccer hail is $12.5.

Module 4 Proportionality in Geometry

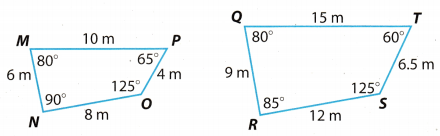
Question 1.
Are the four-sided shapes similar? Explain. (Lesson 4.1)
Answer:
\centering From the picture we can see that:
m∡M = m∡Q = 80°; ∡M corresponds to ∡Q
m∡O = m∡S = 125°; ∡O corresponds to ∡S
\centering AngLes ∡N and ∡P do not correspond to angles ∡R and ∡T.
\(\overline{M P}\) corresponds to \(\overline{Q T}\)
\(\overline{M N}\) corresponds to \(\overline{Q R}\)
\(\overline{N O}\) corresponds to \(\overline{R S}\)
\(\overline{M P}\) corresponds to \(\overline{Q T}\)
\(\overline{P O}\) corresponds to \(\overline{T S}\)
Is it true that \(\frac{M P}{Q T}=\frac{M N}{Q R}=\frac{N O}{R S}=\frac{P O}{T S}\)?
\(\frac{10}{15}=\frac{6}{9}=\frac{8}{12}=\frac{4}{6.5}\)
We get:
0.66 = 0.66 = 0.66 = 0.61
which is not correct, therefore, this four-sided shapes is not similar

Question 2.
△JNZ ~ △KOA. Find the unknown measures. (Lesson 4.2)

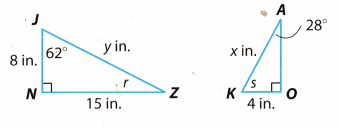
x = ______________
y = ______________
r = ______________
s = ______________
Answer:
To find y, we use Pythagoras theorem:
a² + b² = c²
where C represents the Length of the hypotenuse and a and b the lengths of the triangLes other two sides.
y² = 8² + 15²
y² = 64 + 225
y² = 289 Root both side
\(\sqrt{y^{2}}=\sqrt{289}\)
y = 17
These two shapes are similar, so the corresponding sides are proportional.
Write the proportion.

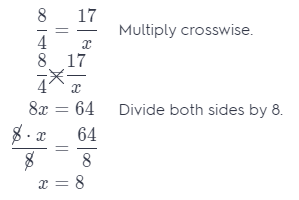
The sum of angles in a triangle is 180°.
Hence
62° + 90° + r = 180°
152° + r = 180° Subtract 152° from both sides
r = 180° – 152°
r = 28°

28° + 90° + s = 180°
118° + s = 180° Subtract 118° from both sides.
s = 180° – 118°
s = 62°

Question 3.
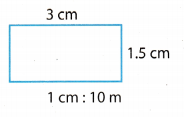
In the scale drawing of a park, the scale is 1 cm: 10 m. Find the area of the actual park. (Lesson 4.3)

Answer:
1 centimeter in this drawing equals 10 meters oo the actual park.
Find the length of the actual park.
MuLtiply 3 by 10.
3 ∙ 10 = 30 m
Find a width of actual park.
Multiply 1.5 by 10.
1.5 ∙ 10 = 15
The area of the actual park find from formula for the area of rectangle P = l ∙ w.
P = 30 ∙ 15 = 450 m²

Question 4.
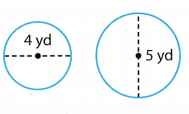
The circumference of the larger circle is 1 5.7 yards. Find the circumference of the smaller circle. (Lesson 4.4)

Answer:
C₁ = the circumference of the larger circle
C₂ = the circumference of the smaller circle
d₁= the diameter of the larger circle
d₂ = the diameter of the smaller circle
Two circles are similar, so the corresponding measures are proportional.
Write the proportion.

The circumference of the smaller circle is 12.56 yards.

Texas Go Math Grade 7 Unit 2 Performance Tasks Answer Key

Question 1.
CAREERS IN MATH Landscape Architect A landscape architect creates a scale drawing of her plans for a garden. She draws the plans on a sheet of paper that measures 8\(\frac{1}{2}\) inches by 11 inches. On the right- hand side of the paper, there is a column 2\(\frac{1}{2}\) inches wide that includes the company name and logo. The drawing itself is 5\(\frac{1}{2}\) inches by 7\(\frac{1}{2}\) inches. The scale of the drawing is 1 inch = 10 feet.

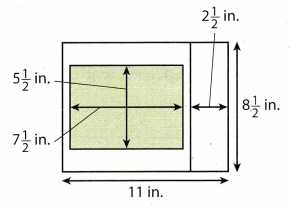
a. The landscape architect wants to make a larger drawing on a sheet of paper that measures 11 inches by 17 inches. The larger drawing should include the same 2\(\frac{1}{2}\) inch column on the side. There should be at least \(\frac{1}{2}\) inch of space on all sides of the drawing. What are the dimensions of the area she can use to make the new drawing?
Answer:
From the 17 inches, the 2\(\frac{1}{2}\) inches removed for the area of the sketch there is 14\(\frac{1}{2}\) Removing the \(\frac{1}{2}\) inch for the border, the dimensions of the area will be 10 inches by 13\(\frac{1}{2}\) inches. The sketch of the dimensions for the 11 inches by 17 inches is:

b. How large can she make the scale drawing without changing any of the proportions? Justify your reasoning.
Answer:
Determine how large the scale drawing can be without changing the proportion. Let x be the length of the other side.
\(\frac{5.5}{7.5}\) = \(\frac{x}{13.5}\) Set up the proportion
74.25 = 7.5x Cross multiply
\(\frac{74.25}{7.5}\) = \(\frac{7.5x}{7.5}\) Divide both sides by 7.5
9.9 = x Simplify

Question 2.
The table below shows how far several animals can travel at their maximum speeds in a given time.

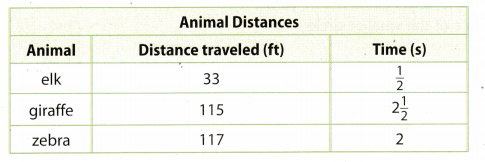
a. Write each animal’s speed as a unit rate in feet per second.
Answer:
Elk travels 33 ft in \(\frac{1}{2}\) seconds.
To find the unit rate in feet per second, divide the distance by time.
33 ÷ \(\frac{1}{2}\) = 33 ∙ 2 = 66
Speed of elk is 66 ft/second.
Giraffe travels 115 ft in 2\(\frac{1}{2}\) seconds.
To find the unit rate in feet per second, divide the distance by time.
115 ÷ 2\(\frac{1}{2}\) = 115 ÷ \(\frac{5}{2}\) = 115 ÷ 2.5 = 46
Speed of giraffe is 46 ft/second.
Zebra travels 117 ft in 2 seconds.
To find the unit rate in feet per second, divide the distance by time.
117 ÷ 2 = 117 ÷ 2 = 58.5
Speed of zebra is 58.5 ft/second.

b. Which animal has the fastest speed?
Answer:
The elk is fastest animal.

c. How many miles could the fastest animal travel in 2 hours if it maintained the speed you calculated in part a? Use the formula d = rt and round your answer to the nearest tenth of a mile. Show your work.
Answer:
First, convert 2 hours to seconds, and 66 ft/second to miles/second
1 foot = 0.00019 miles
1 hours = 3600 seconds
2 hours = 2 3600 = 7200 seconds
66 ft/s = 66 0.00019 = 0.0 12 mi/s
d = r ∙ t Substitute 0.012 for r and 7200 for t.
d = 0.012 ∙ 7200
d = 86.4
The fastest animal, in this case elk, travels 86 miles in 2 hours.

d. The data in the table represents how fast each animal can travel at its maximum speed. Is it reasonable to expect the animal from part b to travel that distance in 2 hours? Explain why or why not.
Answer:
Yes, it is reasonable, because the average top speed of the elk is about 45 miles per hour.

Texas Go Math Grade 7 Unit 2 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
If the relationship between distance y in feet and time x in seconds is proportional, which rate is represented by \(\frac{y}{x}\) = 0.6?
(A) 3 feet in 5 s
(B) 3 feet in 9 s
(C) 10 feet in 6 s
(D) 18 feet in 3 s
Answer:
(A) 3 feet in 5 s

Explanation:
Variable x represents time in seconds.
Variable y represents distance in feets.
We need to get. that x divided by y is 0.6.
check answer under (A) when we substitute value for x and y.

Rate represented by \(\frac{x}{y}\) = 0.6 is under (A) 3 feet in 5 second.

Question 2.
The Baghrams make regular monthly deposits in a savings account. The graph shows the relationship between the number x of months and the amount y in dollars in the account.

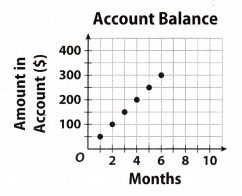
What is the equation for the deposit?
(A) \(\frac{y}{x}\) = $25/month
(B) \(\frac{y}{x}\) = $40/month
(C) \(\frac{y}{x}\) = $50/month
(D) \(\frac{y}{x}\) = $75/month
Answer:
(C) \(\frac{y}{x}\) = $50/month

Explanation:
For 1 month, the amount in account is $50.
Hence.
\(\frac{y}{x}\) = \(\frac{50}{1}\) = $50/month

For 2 month, the amount in account is $100.
Hence,
\(\frac{y}{x}\) = \(\frac{100}{2}\) = $50/month

For 3 month, the amount in account is $150.
Hence,
\(\frac{y}{x}\) = \(\frac{150}{3}\) = $50/month
The answer is \(\frac{y}{x}\) = \(\frac{50}{1}\) = $50/month.

Hot Tip! Read graphs and diagrams carefully. Look at the labels for important information.

Question 3.
Rosa’s room is 4 meters wide. Which of these is an equivalent measurement?
(A) 0.28 mile
(B) 4.38 yards
(C) 12.4 feet
(D) 136.2 inches
Answer:
(B) 4.38 yards

Explanation:
\centering As we know:
0.39 = \(\frac{1}{2.54}\) inch ≈ 1 centimeters
3.28 = \(\frac{1}{0.305}\) foot ≈ 1 meters
1.094 = \(\frac{1}{0.914}\) yard ≈ 1 meters
0.62 = \(\frac{1}{1.61}\) mile ≈ 1 kilometers

One meter has 100 centimeters. so. four meters have 400 centimeters.
Multiply 0.39 by 100 to obtain how much inches is in four meters.
0.39 ∙ 400 = 156 inches
Therefore, the answer under (D) is not correct.
To obtain how much feet is in four meters, multiply 3.28 by 4.
3.28 ∙ 4 = 13.12 ft
Therefore, the answer under (C) is not, correct.
To obtain how much yards is in four meters, multiply 1 .094 by 4.
1.091 ∙ 1 = 4.38 yards
Therefore, the answer under (B) is correct.
One kilometer has 1000 meters. so. four kilometers have 4000 meters.
To obtain how much miles is in four meters, multiply 0.62 by 4000.
0.62 ∙ 4000 = 2480 miles
Therefore, the answer under (A) is not correct.

Question 4.
What is the decimal form of -4\(\frac{7}{8}\)?
(A) -4.9375
(B) -4.875
(C) -4.75
(D) -4.625
Answer:
(B) -4.875

Explanation:
First, convert whole number 4 to eights and add \(\frac{7}{8}\).
\(-\frac{4 \cdot 8+7}{8}=-\frac{32+7}{8}=-\frac{39}{8}\) = -4.875.

Question 5.
Find the percent change from 72 to 90.
(A) 20% decrease
(B) 20% increase
(C) 25% decrease
(D) 25% increase
Answer:
(D) 25% increase

Explanation:
First we find amount of change.
Amount of Change = Greater Value Lesser Value
= 90 – 72
= 18
Now, we have all necessary data to find percent change.

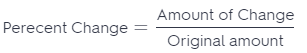
= \(\frac{18}{72}\)
= \(\frac{1}{4}\)
= 0.25 = 25%

Question 6.
A store had a sale on art supplies. The price p of each item was marked down 60%. Which expression represents the new price?
(A) 0.4p
(B) 0.6p
(C) 1.4p
(D) 1.6p
Answer:
(A) 0.04p

Explanation:
Because the price of each item decreases 60%, the new price of each item is 40% of price p.
40% as a decimal. is 0.4.
Hence, the new price for each item is 0.04p.

Question 7.
Clarke borrows $ 16,000 to buy a car. He pays simple interest at an annual rate of 6% over a period of 3.5 years. How much does he pay altogether?
(A) $18,800
(B) $19,360
(C) $19,920
(D) $20,480
Answer:
(B) $19,360

Explanation:
6 % in decimal amounts 0.06.
We are searching for an amount of simple interest for one year.
Multiply 0.06 by 16, 000.
0.06 ∙ 16000 = $960
To find for 3.5 years, multiply the result by 3.5.
960 ∙ 3.5 = $3,360
Altogether he pay:
16,000 + 3,360 = $19,360

Question 8.
To which set or sets does the number 37 belong?
(A) integers only
(B) rational numbers only
(C) integers and rational numbers only
(D) whole numbers, integers, and rational numbers
Answer:
(D) whole numbers, integers, and rational numbers

Explanation:
Number 37 is whole number, integer and rational number.

Question 9.
The two triangles below are similar. What is the missing length?

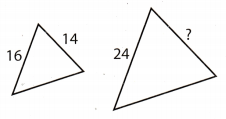
(A) 21
(B) 22
(C) 24
(D) 26
Answer:
(A) 21

Explanation:
a₁ = 14
b₁ = 16
a = ?
b = 24
\centering To find the missing Length, use a proportion

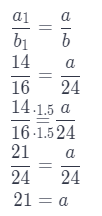
Gridded Response

Question 10.
The smaller circle has a diameter that is half the size of the larger circle. What is the missing circumference in centimeters?

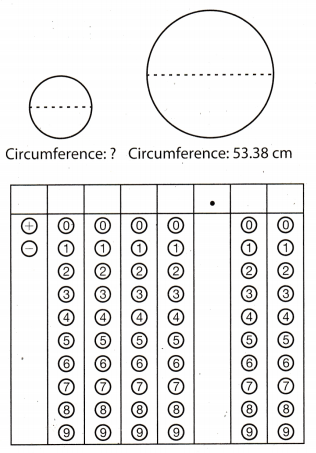
Answer:
C₁ = the circumference of the larger circle
C₂ = the circumference of the smaller circle
d₁ = the diameter of the larger circle
d₂ = the diameter of the smaller circle
The diameter of the smaller circle is half the diameter of the larger circle.
Hence
d₁ = 2d₂
Two circles are similar, so the corresponding measures are proportional.
Write the proportion.
\(\frac{C_{1}}{C_{2}}=\frac{d_{1}}{d_{2}}\) Substitute 53.38 for C_1, 2d₂ for d₁.
\(\frac{53.38}{C_{2}}=\frac{d_{2}}{d_{2}}\)
\(\frac{53.38}{C_{2}}\) = 2
C₂ = \(\frac{53.38}{2}\)
C₂ = 26.69
The circumference of the smaller circle is 26.69 cm.

Question 11.
Jermaine paid $37.95 for 11 gallons of gasoline. What was the price in dollars per gallon?

Answer:
To find a price in dollars per gallon, divide $37.95 by 11.

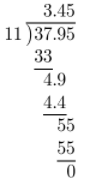
Therefore, each gallon cost $3.45.

Hot Tip! Pay attention to the units given in a test question, especially if there are mixed units, such as inches and feet.

Question 12.
Shown below is a scale drawing of a rectangular patio.

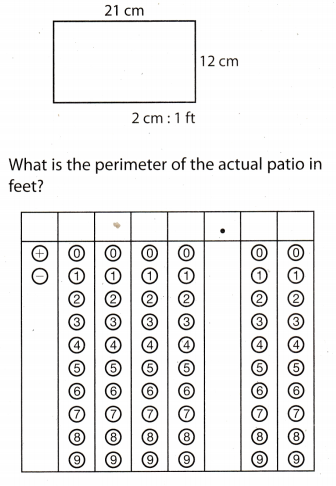
Answer:
2 cm : 1 ft ⇔ 1 cm : \(\frac{1}{2}\) ft
P = perimeter of a rectangle
l = 21 cm
w = 12 cm
Use the formula for perimeter of rectangle.
P = 2(l + w) Substitute 21 for l and 12 for w.
P = 2(21 + 12)
P = 2.33
P = 66 cm
Because 1 cm : \(\frac{1}{2}\) ft, the perimeter of the actual patio is 66 ∙ \(\frac{1}{2}\) = 33 ft.

Texas Go Math Grade 7 Unit 2 Vocabulary Preview Answer Key

Use the puzzle to preview key vocabulary from this unit. Unscramble the circled letters within found words to answer the riddle at the bottom of the page.

1. A relationship between two quantities in which the rate of change or the ratio of one quantity to the other is constant. (Lesson 2-2)

2. Describes how much a quantity decreases in comparison to the original amount. (Lesson 3-2)

3. A fixed percent of the principal. (Lesson 3-4)

4. Angles of two or more similar shapes that are in the same relative position. (Lesson 4-1)

5. A proportional two-dimensional drawing of an object. (Lesson 4-3)

Question.
What did the athlete order when he needed a huge helping of mashed potatoes?
Answer:
_____ ____ ____ ____ – ____ ____ ____ ____ ____ ____ ____!