Texas Go Math Grade 7 Module 10 Quiz Answer Key

Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Module 10 Quiz Answer Key.

Texas Go Math Grade 7 Module 10 Quiz Answer Key

Texas Go Math Grade 7 Module 10 Ready to Go On? Answer Key

10.1 Volume of Rectangular Prisms and Pyramids

Find the volume of each figure.

Question 1.

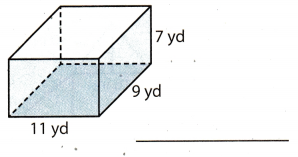
Answer:
l = 11 yd length of base
w = 9 yd Width of base
h = 7 yd Height of a prism
Find the area of the base B. A prism has a base that is rectangular, so use the formula:
B = l.w = 11.9 = 99 yd²
Use the formula for the volume of a rectangular prism.
V = B.h = 99 . 7 = 693 yd³

The volume of a rectangular prism is 693 yd³.

Question 2.

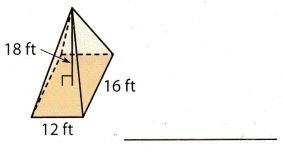
Answer:
l = 12 ft length of base
w = 16 ft Width of base
h = 18 ft Height of a pyramid

Find the area of the base B.

B = l . w = 12 . 16 = 192 ft²
Use the formula for the volume of a rectangular pyramid.

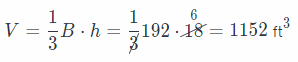
The volume of a rectangular pyramid is 1152 ft³.

The volume of a rectangular pyramid is 1152 ft³.

10.2 Volume of Triangular Prisms and Pyramids

Find the volume of each figure.

Question 3.

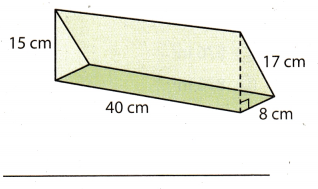
Answer:
A prism has a base that is right triangle.
a = 8 cm length of one side of the triangle
b = 17 cm length of other side of the triangle
Find the area of the base B. Use the formula:

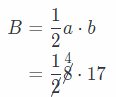
B = 68 cm² Base of prism
h = 40 cm Height of a prism
Use the formula.
V = B . h = 68 . 40 = 2720 cm³
The volume of a triangular prism is 2720 cm³.

Question 4.

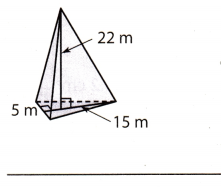
Answer:
b = 5 m length of base
h_B = 15 m height of base
h = 22 m Height of a pyramid
Find the area of the base B. Use the formula:
B = \(\frac{1}{2}\) . b . h_B = \(\frac{1}{2}\) . 5 . 15 = 37.5 m²
Use the formula for the voLume of a triangular pyramid:
V = \(\frac{1}{3}\)B . h = \(\frac{1}{3}\) . (37.5) . 22 = 275 m³
The volume of a triangular pyramid is 275 m³.

10.3 Lateral and Total Surface Area

Find the lateral and total surface area of each figure using its net.

Question 5.

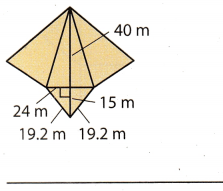
Answer:
Find the Lateral area of the triangular pyramid.
We have three triangles with base of 19.2 m. and height of 40 m.
b = 19.2 m length of base
h_B = 40 m Height of base
Lateral area:

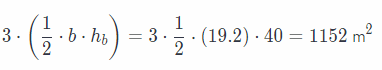
For the area of the base:
b = 24 m length of base
h_b = 15 m Height of base
The area of the base is

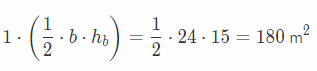
The total surface area is 1152 + 180 = 1332 m²

The Lateral area is 1152 m².
The total surface area is 1332 m².

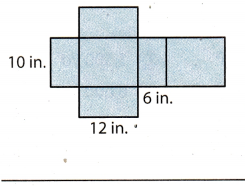
Question 6.

Answer:
Find the Lateral area of the rectangular prism.
We have:
Two 12 in. by 6 in. rectangle;
Two 10 in. by 6 in. rectangle;
2 . (12 . 6) = 144
2 . (10 . 6) = 120
Lateral area: 144 + 120 = 264 cm²
Each base is 12 in. by 10 in.
2 . (12 . 10) = 2 . 120 = 240 cm²
The total surface area is 264 + 240 = 504 cm².

The Lateral area is 264 cm.
The total surface area is 504 cm².

Essential Question

Question 7.
How can you use volume and surface area to solve real-world problems?
Answer:
Volume and surface area can be used in many ways to solve the real-world problems such as:
For example we are making a new thing of copper and we know the volume of that thing so we can know the exact amount of copper required for making that thing by using the density = \(\begin{gathered}
\text { Mass } \\
\hline \text { Volume }
\end{gathered}\)of copper

In another example suppose a wall is to be painted and the cost of paint one square meter of wall is given then we can easily calculate the total cost for painting wall by using the total surface area of wall.

Volume can be use for calculating amount of material required for making something.

Texas Go Math Grade 7 Module 10 Mixed Review Texas Test Prep Answer Key 

Selected Response

Question 1.
The volume of a triangular pyramid is 232 cubic units. The area of the base of the pyramid is 29 square units. What is the height of the pyramid?
(A) 8 units
(B) 12 units
(C) 16 units
(D) 24 units
Answer:
(D) 24 units

Explanation:
Use formula for the volume of a triangular pyramid.
B = 29 square units Base of pyramid
h = ? Height of a pyramid
V = 232 cubic units The volume of a pyramid
Use the formula for the volume of a pyramid to find a height of the pyramid.
V = \(\frac{1}{3}\) . B . h.
232 = \(\frac{1}{3}\) . 29 . h
232 = (9.66) . h
Divide both sides by 9.66.

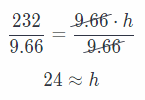
The height of pyramid is 24 units

Question 2.
What is the volume of a rectangular prism that has a length of 8.5 centimeters (cm), a width of 3.2 centimeters, and a height of 6 centimeters?
(A) 19.2 cm³
(B) 27.2 cm³
(C) 51 cm³
(D) 163.2 cm³
Answer:
(D) 163.2 cm³

Explanation:
h = 6 cm Height of prism
l = 8.5 cm Length of base
w = 3.2 cm Width of base
Use the formula for the volume of a rectangular prism
V = B . h = l . w . h
= (8.5) (3.2) . h
= (27.2) . 6
= 163.2 cm³
The volume of a rectangular prism is V = 163.2 cm³

Question 3.
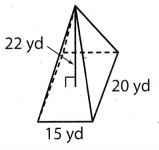
What is the volume of the rectangular pyramid shown?

(A) 1,650 yd³
(B) 2,200 yd³
(C) 3,300 yd³
(D) 6,600 yd³
Answer:
h = 22 yd Height of pyramid
l = 15 yd Length of base
w = 20 yd Width of base
Use the formula for the volume of a rectangular pyramid.
V = \(\frac{1}{3}\) . B . h. = \(\frac{1}{3}\) . l . w . h.
= \(\frac{1}{3}\) . 15 . 20 . 22
= 2200 yd³

The volume of the rectangular pyramid is V = 2200 yd³.

Question 4.
A circle has a circumference of 56π centimeters (cm). What is the radius of the circle?
(A) 28 cm
(B) 56 cm
(C) 88 cm
(D) 112 cm
Answer:
(A) 28 cm

Explanation:
Given circumference of circle in probem = 56π cm
We know that circumference of circle of radius “r” = 2π . r
2π . r = 56π (By using above formula)
r = \(\frac{56 \pi}{2 \pi}\) (Dividing both side by 2π)
r = 28 cm (Simplifying)
hence, option A is correct answer.

Question 5.
What is the volume of a triangular prism that has a height of 45 meters and has a base with an area of 20 square meters?
(A) 225 m³
(B) 300 m³
(C) 450 m³
(D) 900 m³
Answer:
(D) 900 m³

Explanation:
h = 45 m Height of a prism
B = 20 m² Base area
Use the formula for the volume of a triangular prism.
V = B . h
= 20 . 45
= 900 m³

The volume of a triangular prism is V = 900 m³.

Question 6.
What is the total surface area of the square pyramid whose net is shown?

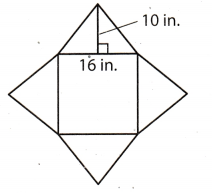
(A) 256 in²
(B) 336 in²
(C) 576 in²
(D) 896 in²
Answer:
(C) 576 in²

Explanation:
For lateral area:
There are four triangles with base of 16 in. and height of 10 in.

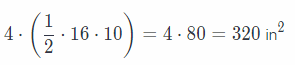
Lateral area: 320 in²
The base has the shape of 16 in. by 16 in. rectangle.
Base area:
1 (16 . 16) = 256 in²
The total surface area is 320 + 256 = 576 in²

The surface area is 576 in².

Gridded Response

Question 7.
What is the lateral area in square meters of the prism?

Answer:
Lateral area of the prism will be the sum of areas of all the surface except base in the given figure.
Length of the rectangle = 18 in
Breadth of the rectangle = 10 m
Base of the triangle = 12 in
Height of the triangle = 8 in
We know that area of the rectangle is = Length × Breadth
We know that area of the triangle is = \(\frac{1}{2}\) × Base × Height
Area of rectangle = 18 × 10 m²
= 180 m²
Area of triangle = \(\frac{1}{2}\) × 12 × 8 m²
= 48 m²

Lateral area of prism = 2 × Area of rectangle + 2 × Area of triangle
= (2 × 180) + (2 × 48)
= 360 + 96
= 456 m²

Hence, lateral area of the prism is 456 m²

Steps to plot the given box are:
In 1^st column : mark “+” sign
In 2^nd column : mark “0”
In 3^rd coumn: mark “4”
In 4^th column : mark “5”
In 5^th column : mark “6”
In 6^th column : mark “0”
In 7^th column : mark “0”

Lateral area of the prism is 456 m²