Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 9.1 Answer Key Angle Relationships.
Texas Go Math Grade 7 Lesson 9.1 Answer Key Angle Relationships
Essential Question
How can you use angle relationships to solve problems?
Texas Go Math Grade 7 Lesson 9.1 Explore Activity Answer Key
Measuring Angles
It is useful to work with pairs of angles and to understand how pairs of angles relate to each other. Congruent angles are angles that have the same measure.
Step 1
Using a ruler, draw a pair of intersecting lines. Label each angle from 1 to 4.
Step 2
Use a protractor to help you complete the chart.
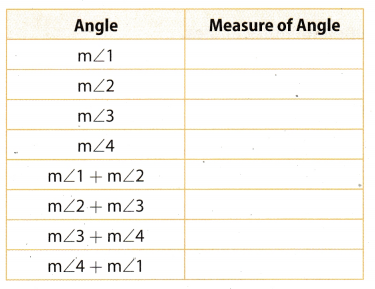
Reflect
Question 1.
Conjecture Share your results with other students. Make a conjecture about pairs of angles that are opposite each other.
Answer:
The measures of the vertical opposite angles are equal, so we have two pairs of angles with the same measure.
Question 2.
Conjecture When two lines intersect to form two angles, what conjecture can you make about the pairs of angles that are next to each other?
Answer:
Every pair of angles, obtained by the intersection of two lines, that are next to each other form a straight line, or an angle of 180°. Hence, they are supplementary angles.
Example 1
Use the diagram.
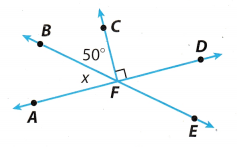
A. Name a pair of vertical angles.
∠AFB and ∠DFE
B. Name a pair of adjacent angles.
∠AFB and ∠BFD
C. Name a pair of supplementary angles.
∠AFB and ∠BFD
D. Find the measure of ∠AFB.
Use the fact that ∠AFB and ∠BFD in the diagram are supplementary angles to find m∠AFB.

The measure of ∠AFB is 40°
Reflect
Question 3.
Analyze Relationships What is the relationship between ∠AFB and ∠BFC? Explain.
Answer:
The measure of ∠DFC is 90°
m∠AFB + m∠BFC + m∠DFC = 180°
m∠AFB + m∠BFC + 90° = 180°
Subtract 90° from both sides
m∠AFB + m∠BFC = 90°
∠AFB and ∠BFC are complementary angles.
∠AFB and ∠BFC are complementary angles.
Question 4.
Draw Conclusions Are ∠AFC and ∠BFC adjacent angles? Why or why not?
Answer:
Yes, they are, because they have a common side, a common vertex(corner point), and they dont overlap.
Your Turn
Use the diagram.
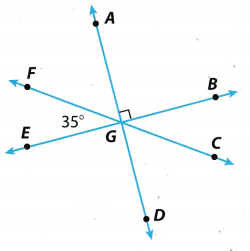
Question 5.
Name a pair of supplementary angles.
Answer:
∠EGF and ∠FGB.
Question 6.
Name a pair of vertical angles.
Answer:
∠FGA and ∠DGC
Question 7.
Find the measure of ∠CGD. ______
Answer:
We see from the diagram that
m∠CGD + m∠DGE + m∠EGF = 180°.
∠DGE and ∠AGB are vertical opposite angles, so their measures are equal.
m∠DGE + m∠AGB = 90°.
m∠CGD + m∠DGE + m∠EGF = 180° Substitute 90° for m∠DGE, and 35° for m∠EGF.
m∠CGD + 90° + 35° = 180°
m∠CGD + 125° = 180° Subtract 125° from both sides.
m∠CGD = 180° – 125°
m∠CGD = 55°
m∠CGD = 55°
Example 2
A. Find the measure of ∠EHF.

Since m∠EHF = 2x, then m∠EHE = 132°
B. Find the measure of ∠ZXY.
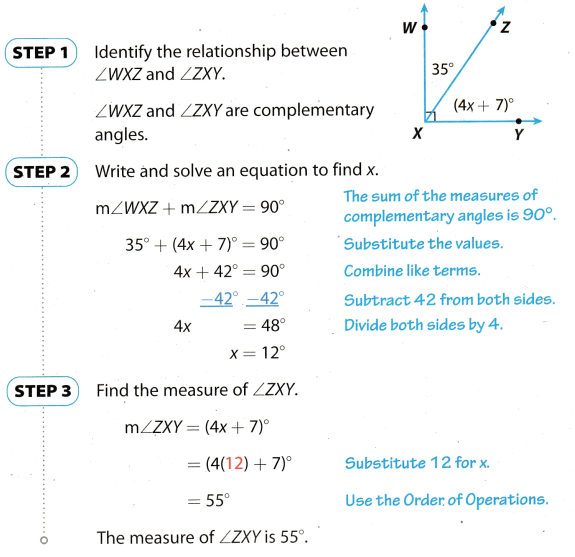
Your Turn
Question 8.
Find the measure of ∠JML.
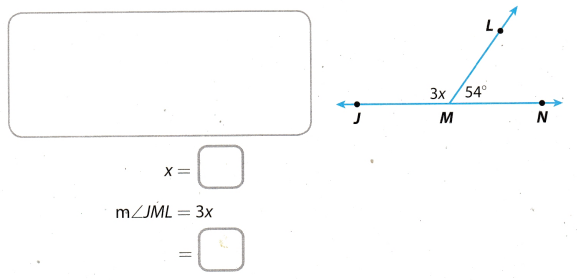
Answer:
From the diagram we see
m∠JML + m∠LMN = 180° Substitute 3x for m∠JML, and 54° for m∠LMN.
3x + 54° = 180° Subtract 54° from both sides.
3x = 180° – 54°
3x = 126° Divide both sides by 3
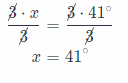
m∠JML = 3x Substitute 41° for x.
m∠JML = 3. 41°
m∠JML = 126°
Question 9.
Critique Reasoning Cory says that to find m∠JML above you can stop when you get to the solution step 3x = 126°. Explain why this works.
Answer:
Both angle ∠JML and ∠LMN are on same straight line and the angle of straight line is 180° So sum of the ∠JML and ∠LMN will be 180° this means both angle are supplementary to each other.
∠JML + ∠LMN = 180°
3x + 54° = 180°
3x + 54 – 54 = 180 – 54
3x = 126°
x = 42°
Hence, 3x = 126° works both angle 3x and 54° are supplementary to each other. So the sum of both the angle will be equal to the 180°
∠JML and ∠LMN are supplementary to each other.
Example 3
The front of the top story of a house is shaped like an isosceles triangle. The measure of the angle at the top of the triangle is 70. Find the measure of each of the base angles.


Your Turn
Use the diagram.
Question 10.
Find the value of x. ____________
Answer:
The sum of the measures of an angles in a triangle is
∠C + ∠A + ∠B = 180° Substitute 800° for ∠C, x for ∠A and 3x for ∠B.
80 + x + 3x = 180°
4x + 80° = 180° Subtract 80° from both sides.
4x = 180° – 80°
4x = 100° Divide both sides by 4.
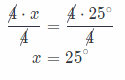
x = 25°
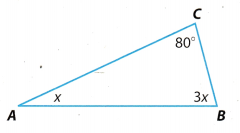
Question 11.
Find the measures of
∠A and ∠B. _____________
Answer:
x = 25°
m∠A = x Substitute 25° for x
m∠A = 25°
m∠B = 3x Substitute 25° for x
m∠B = 3 . 25°
m∠B = 75°
m∠A = 25°, m∠B = 75°
Texas Go Math Grade 7 Lesson 9.1 Guided Practice Answer Key
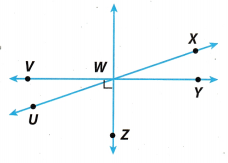
For Exercises 1-2, use the figure. (Example 1)
Question 1.
Vocabulary The sum of the measures of ∠UWV and ∠UWZ is 90°, so ∠UWV and ∠UWZ are ____ angles.
Answer:
Complementary angles
Question 2.
Vocabulary ∠UWV and ∠VWX share a vertex and one side. They do not overlap, so ∠UWV and ∠VWX are
____ angles.
Answer:
Adjacent angles
For Exercises 3-4, use the figure.
Question 3.
∠AGB and ∠DGE are ________________ angles, so m∠DGE= . (Example 1)
Answer:
– Vertical angles.
-m∠DGE = 30°.
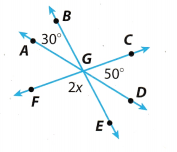
Question 4.
Find the measure of ∠EGF. (Example 2)
m∠CGD + m∠DGE + m∠EGF = 180°
____ + ____ + ____ = 180°
____ + 2x = 180°
2x = _____
m∠EGF = 2x = ___
Answer:
50° + 30° + 2x = 180°
80° + 2x = 180°
2x = 100°
m∠EGF = 2x = 100°
m∠EGF = 100°
Question 5.
Find the measures of ∠A and ∠B. (Example 3)
m∠A + m∠B + m∠C = 180
____ + _______ + ____ = 180
2x + __ = 180

2x = _____
x = __, so, m∠A = ___.
x + 10 = _____, so m∠B = ___.
Answer:
x + x + 10° + 40° = 180°
2x + 50° = 180°
2x = 130°
x = 65°, so m∠A = 65°
x + 10° = 75°, so m∠A = 75°
m∠A = 65° m∠B = 75°
Essential Question Check-In
Question 6.
Suppose that you know that ∠T and ∠S are supplementary, and that m∠T = 3 . (m∠S). How can you find m∠T?
Answer:
∠T and ∠S are supplementary, so they form an angle of 180°
m∠T = 180°
m∠T + m∠S = 180°
3(m∠S) + m∠S = 180°
4 . m∠S = 180° Divide both sides by 4.

m∠T = 3 . 45° = 125°
Texas Go Math Grade 7 Lesson 9.1 Independent Practice Answer Key
For Exercises 7-11, use the figure.
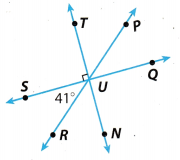
Question 7.
Name a pair of adjacent angles. Explain why they are adjacent.
Answer:
∠RUS and ∠SUT because they have a common side and a common vertex.
Question 8.
Name a pair of acute vertical angles.
Answer:
∠RUS and ∠QUP
Question 9.
Name a pair of supplementary angles.
Answer:
∠TUP and ∠PUN
Question 10.
Justify Reasoning Find m∠QUR. Justify your answer.
Answer:
∠QUR and ∠RUS are supplementary angles, so
m∠QUR + m∠RUS = 180° Substitute 41° for both sides
m∠QUR + 41° = 180° Subtract 41° from both sides.
m∠QUR = 180° – 41°
m∠QUR = 139°
Question 11.
Draw Conclusions Which is greater, m∠TUR or m∠RUQ? Explain.
Answer:
From the diagram we see
m∠TUR = m∠TUS + m∠RUS
m∠RUQ = m∠NUQ + m∠RUN
∠TUS and ∠NUQ are vertical opposite angles, so their measures are equal.
m∠TUS = m∠NUQ = 90°
∠RUN and ∠RUS are complementary angles, so they form an angle of 90°
Since m∠RUS = 41°, we have
m∠RUS + m∠RUN = 90° Substitute 41° for ∠RUS.
41° + m∠RUN = 90° Subtract 41° from both sides
m∠RUN = 90° – 41°
m∠RUN = 49°
Put these reasults into the following:
m∠TUR = m∠TUS + m∠RUS
m∠TUR = 90° + 41°
m∠TUR = 131°
m∠RUQ = m∠NUQ + m∠RUN
m∠RUQ = 90° + 49°
m∠RUQ = 139°
m∠TUR < m∠RUQ
m∠RUQ is greater than m∠TUR
Solve for each indicated angle measure or variable in the figure.
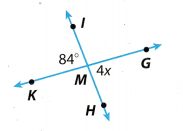
Question 12.
x ____________
Answer:
∠KMI and ∠HMG are vertical opposite angles, so they have the same measure.
4x = 84° Divide both sides by 4.

x = 21°
Question 13.
m∠KMH _______
Answer:
m∠KMH and m∠KMI are supplementary angles
m∠KMH – m∠KMI = 180° Substitute 84° for ∠KMI.
m∠KMH + 84° = 180° Subtract 84° from both sides
m∠KMH = 180° – 84°
m∠KMH = 96°
Solve for each indicated angle measure or variable in the figure.

Question 14.
m∠CBE ______
Answer:
m∠CBE and m∠EBF are supplementary angles.
m∠CBE + m∠EBF = 180° Substitute 62° for ∠EBF.
m∠CBE + 62° = 180° Subtract 62° from both sides.
m∠CBE = 180° – 62°
m∠CBE = 118°
Question 15.
m∠ABF _____
Answer:
m∠ABF and m∠FBE are complementary angles.
m∠ABF + m∠FBE = 90° Substitute 62° for ∠FBE.
m∠ABF + 62° = 90° Subtract 62° from both sides.
m∠ABF = 90° – 62°
m∠ABF = 28°
Question 16.
m∠CBA _____
Answer:
m∠CBA and m∠ABF are supplementary angles.
m∠CBA + m∠ABF = 180° Substitute 28° for ∠ABF.
m∠CBA + 28° = 180° Subtract 28° from both sides.
m∠CBA = 180° – 28°
m∠CBA = 152°
Solve for each indicated angle measure or variable in the figure.
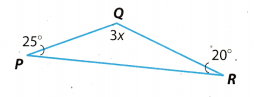
Question 17.
x ___________
Answer:
The sum of the measures of an angles in a triangle is 180°, so we have
∠P + ∠Q + ∠R = 180° Substitute 25° for ∠P, 3x for ∠Q and 20° for ∠R.
25° + 3 + 20° = 180°
3x + 45° = 180° Subtract 45° from both sides.
3x = 180° – 45°
3x = 135° Divide both sides by 3.
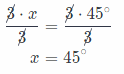
Question 18.
m∠Q _______
Answer:
x = 45°
m∠Q = 3x Supstitute 45° for z.
= 3 . 45°
= 135°
Texas Go Math Grade 7 Lesson 9.1 H.O.T. Focus on Higher Order Thinking Answer Key
Let ∆ABC be a right triangle with m∠C = 90°.
Question 19.
Critical Thinking An equilateral triangle has three congruent sides and three congruent angles. Can ∆ABC be an equilateral triangle? Explain your reasoning.
Answer:
In given triangle ABC one angle is m∠C = 90° so the triangle ABC cannot be a equilateral triangle. Because in
equilateral triangle all three sides and angle are congruent to each other. So each angle of equilateral triangle is
60° because sum of all the interior angle of triangle is 180°. Hence each angle of equilateral triangle is \(\frac{180}{3}\) = 60°.
Thus the given triangle ABC cannot be a equilateral triangle.
Given triangle ABC cannot be a equilateral triangle.
Question 20.
Counterexample An isosceles triangle has two congruent sides, and the angles opposite those sides are congruent. River says that right triangle ABC cannot be an isosceles triangle. Give a counterexample to show that his statement is incorrect.
Answer:
There is a special right triangle that can be considered as an isosceles triangle. This is the 45° right triangle wherein, the two sides have 45° angles. The measure of the sides are congruent and the angles are also congruent.
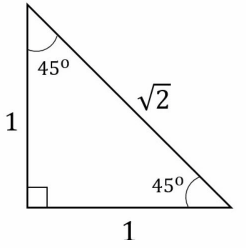
The 45° right triangle is an isosceles triangle.
Question 21.
Make a Conjecture In a scalene triangle, no two sides have the same length, and no two angles have the same measure. Do you think a right triangle can be a scalene triangle? Explain your reasoning.
Answer:
Any right triangle can be a scalene triangle except for the 45°-45° right triangle. This is because the two angles of
a right triangle can be of any measure for as long as the total of the two angles is 90°. The measurement of the
sides of the right triangle will also vary.
Yes
Question 22.
Represent Real-World Problems The railroad tracks meet the road as shown. The town will allow a parking lot at angle J if the measure of angle J is greater than 38°. Can a parking lot be built at angled? Why or why not?
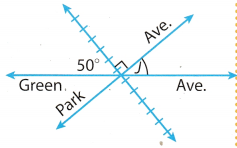
Answer:
All the upper angles are on straight line so they must be supplementary to each other, thus there sum will be equal to 180°
50° + 90° + J = 180°
140° + J = 180°
J = 180 – 140
J = 40°
It is given in the problem that the minimum required angle J for parking lot should be the greater than 38° and we have found that angle J is 40°. So parking lot can be built there.
Hence, parking lot can be built there because angle J is 40°
Question 23.
Analyze Relationships In triangle XYZ, m∠X = 30°, and all the angles have measures that are whole numbers. Angle Y is an obtuse angle. What is the greatest possible measure that angle Z can have? Explain your answer.
Answer:
In triangle XYZ, m∠X = 30° so the sum of remaining angles ∠Y and ∠Z will be 180 – 30 = 150°. Since ∠Y is
an obtuse angle and all angle measures whole number, so minimum value of ∠Y will be 91°. And in equation
∠Y + ∠Z = 180° if ∠Y is minimum than ∠Z must be maximum. Thus maximum value of ∠Y = 150 – 91 = 59°.
Hence, the greatest possible measure of angle Z is 59°.