Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 8.4 Answer Key Solving Two-Step Inequalities.
Texas Go Math Grade 7 Lesson 8.4 Answer Key Solving Two-Step Inequalities
Your Turn
Use algebra tiles to model and solve each inequality.
Question 1.
2x + 7 > 11 ____
Answer:
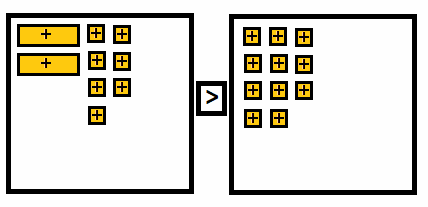
Subtract 7 from both sides.
2x + 7 – 7 > 11 – 7
2x > 4 Divide both sides by 2.
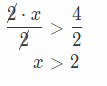
Question 2.
5h – 4 ≥ 11
Answer:
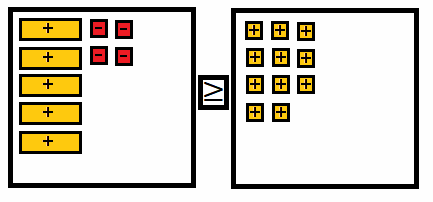
Add 4 to both sides.
5h – 4 + 4 ≥ 11 + 4
5h ≥ 15 Divide both sides by 5.
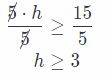
Your Turn
Question 3.
Joshua wants to complete the first mile of a 5-mile run in 10 minutes or less running at a steady pace. The inequality 5 – \(\frac{p}{6}\) ≤ 4 can be used to find p, the pace, in miles per hour, he can run to reach his goal. Solve the inequality. Then graph and interpret the solution.
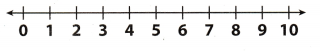
Answer:
Multiply both sides by 6. Because we are multiplying by a negative number, we have to reverse direction of the
inequality.
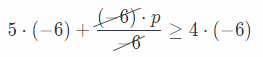
-30 + 9 ≥ -24 Add 30 to the both sides
30 – 30 + p ≥ 30 – 24
p ≥ 6
p ≥ 6
Your Turn
Circle any given values that make the inequality true.
Question 4.
3v – 8 > 22
v = 9; v = 10; v = 11
Answer:
Substitute 9 for v in the given equation.
v = 9
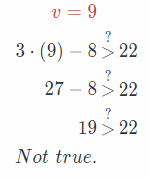
Substitute 10 for v in the given equation.
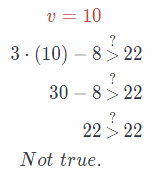
Substitute 11 for v in the given equation.
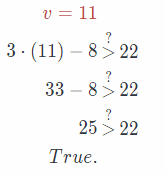
v = 11
Question 5.
5h + 12 ≤ -3
h = -3; h = -4; h = -5
Answer:
Substitute -3 for h in the given equation.
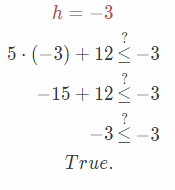
Substitute -4 for h in the given equation.
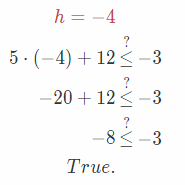
Substitute -5 for h in the given equation.
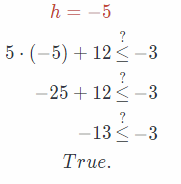
h = -3,
h = -4,
h = -5
Texas Go Math Grade 7 Lesson 8.4 Guided Practice Answer Key
Question 1.
Describe how to solve the inequality 3x + 4 < 13 using algebra tiles. (Example 1)
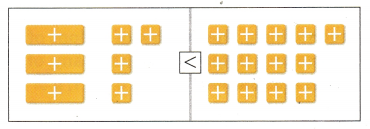
Answer:
Remove 4 + 1 tiles from each side on the mat.
Then, divide each side into 3 equal groups.
3x < 13 – 4
3x < 9 Divide both sides by 3.
\(\frac{3 x}{3}\) < \(\frac{9}{3}\)
x < 3
The solution is x < 3.
Solve each inequality. Graph and check the solution. (Example 2)
Question 2.
5d – 13 < 32 ____
Answer:
Add 13 to the both sides.
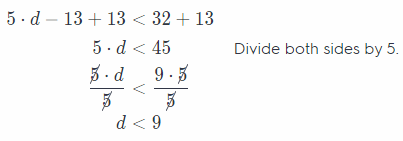
Check the solution for d < 9. For example, d = 5.
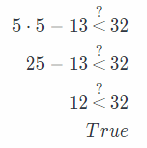
d < 9
Question 3.
-4b + 9 < -7 _____
Answer:
Subtract 9 to the both sides.
Check the solution for b ≥ 4. For example, b = 5.
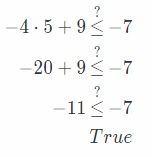
b ≥ 4
Circle any given values that make the inequality true. (Example 3)
Question 4.
2m + 18 > -4
m = -12;m = -11; m = -10
Answer:
Substitute -12 for m in the given equation.
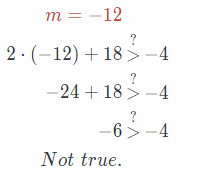
Substitute -11 for m in the given equation.
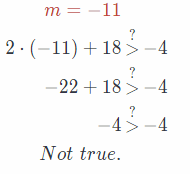
Substitute -10 for m in the qiven equation.
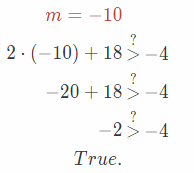
m = -10
Question 5.
-6y + 3 ≥ 0
y = 1; y = \(\frac{1}{2}\); y = 0
Answer:
Substitute 1 for y in the given equation.
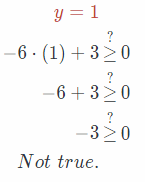
Substitute 1/2 for y in the given equation.
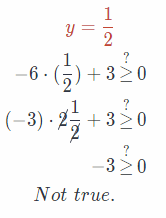
Substitute 0 for y in the given equation.
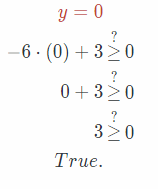
y = 0
Question 6.
Lizzy has 6.5 hours to tutor 4 students and spend 1.5 hours in a lab. She plans to tutor each student the same amount of time. The inequality 6.5 – 4t ≥ 1.5 can be used to find t, the amount of time in hours Lizzy could
spend with each student. Solve the inequality. Graph and interpret the solution. Can Lizzy tutor each student for
1.5 hours? Explain. (Example 2 and 3)
Answer:
Subtract 6.5 from the both sides.
-6.5 + 6.5 – 4t ≤ -6.5 + 1.5
-4f ≤ 4 Divide both sides by -4.
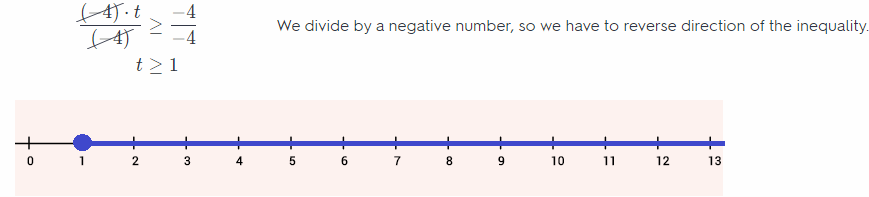
Substitute 1.5 for t in the given equation.
t = 1.5
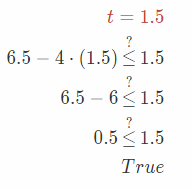
t ≥ 1
Essential Question Check-In
Question 7.
How do you solve a two-step inequality?
Answer:
First, isolate the variable. On one side of the inequality we put the variable, and on other side we put what’s left.
If the variable is multiplied by some number, we have to divide inequality by that number.
If we divide or multiply by a negative number, we have to reverse the direction of inequality.
Texas Go Math Grade 7 Lesson 8.4 Independent Practice Answer Key
Solve each inequality. Graph and check the solution.
Question 8.
2s + 5 ≥ 49
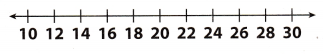
Answer:
Divide both side by 2.
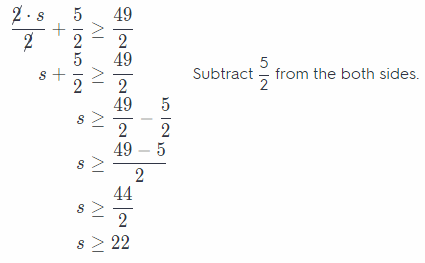
Check the solution for s ≥ 22. For example, s = 23.
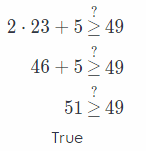
The solution is shown in graph
s ≥ 22
Question 9.
-3f + 9 ≥ -21
Answer:
Subtract 9 from the both sides.
-3t + 9 – 9 ≥ -21 – 9
– 3t > -30 Divide both sides by (-3).
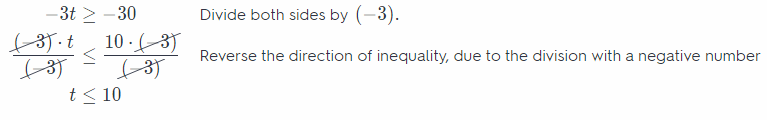
Check the solution for t ≤ 10. For example, t = 9.
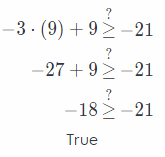
This inequality is shown in the picture.
t ≤ 10
Question 10.
55 > -7v + 6 ____
Answer:
Subtract 6 from the both sides.
55 – 6 > -7v + 6 – 6
49 > -7v Divide both sides by (- 7).
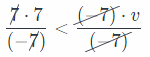Reverse the direction of inequality, due to the division with a negative number
-7 < v Check the solution for v > – 7. For example, v = 6.
55 ⩼ -7 ∙ (-6) + 6
55 ⩼ 42 + 6
55 ⩼ 48
True
This inequality is shown in the picture.
v > -7
Question 11.
41 > 6m – 7 ____
Answer:
Add 7 from the both sides.
41 + 7 > 6m – 7 + 7
48 > 6m Divide both sides by 6.
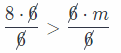
8 > m
Check the solution for in < 8. For example, m = 7.
41 ⩼ 6 . (7) – 7
41 ⩼ 42 – 7
41 ⩼ 35
True
This inequality is shown in the picture.
m < 8 Question 12. \(\frac{a}{-8}\) + 15 > 23
Answer:
Subtract 15 from the both sides.
\(\frac{a}{-8}\) + 15 – 15 > 23 – 15
\(\frac{a}{-8}\) > 8 Multiply both sides by (-8).
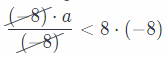Reverse the direction of inequality, due to the division with a negative number
a < -61
Check the solution for a < -64. For example, a = -72.
– \(\frac{-72}{-8}\) + 15 ⩼ 23
9 + 15 ⩼ 23
24 ⩼ 23
True
This inequality is snown in the picture.
a < -64
Question 13.
\(\frac{f}{2}\) – 22 < 48
Answer:
Add 22 from the both sides.
\(\frac{f}{2}\) – 22 + 22 < 48 + 22
\(\frac{f}{2}\) < 70 Multiply both sides by 2.
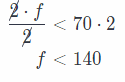
Check the solution for f < 140. For example, f = 130
\(\frac{130}{2}\) – 22 ⩻ 48
65 – 22 ⩻ 48
43 ⩻ 48
True
This inequality is shown in the picture.
f < 140
Question 14.
-25 + \(\frac{t}{2}\) ≥ 50
Answer:
Add 25 from the both sides.
-25 + 25 + \(\frac{t}{2}\) ≥ 50 + 25
\(\frac{t}{2}\) ≥ 75 Multiply both sides by 2.
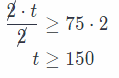
Check the solution for t ≥ 150. For example, t = 160.
-25 + \(\frac{160}{2}\) ⩼ 50
-25 + 80 ⩼ 50
55 ⩼ 50
True
This inequality is shown in the picture.
t ≥ 150
Question 15.
10 + \(\frac{g}{-9}\) > 12
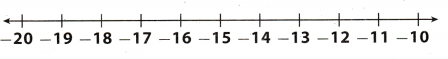
Answer:
Subtract -10 from
10 – 10 + \(\frac{g}{-9}\) > 12 – 10
\(\frac{g}{-9}\) > 2 Multiply both sides by (-9).
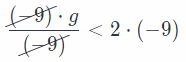Reverse the direction of inequality, due to the multiplication with a negative number
g < -18
Check the solution for g < -18. For example, g = -27
10 + \(\frac{-27}{-9}\) ⩼ 12
10 + 3 ⩼ 12
13 ⩼ 12
True
This inequality is shown in the picture.
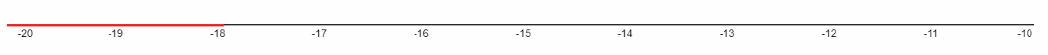
g < -18
Question 16.
25.2 ≤ -1.5y + 1.2.
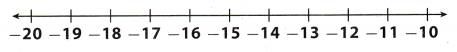
Answer:
Subtract 1.2 from the both sides.
25.2 – 1.2 ≤ -1.5y + 1.2 – 1.2
24 ≤ —1.5y Divide both sides by (-1.5).
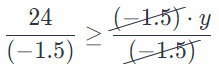Reverse the direction of inequality, due to the division with a negative number
-16 ≥ y
y ≤ -16
Check the solution for y ≤ -16. For example, y = -18.
25.2 ⩻ (-1.5) . (-18) + 1.2
25.2 ⩻ 27 + 1.2
25.2 ⩻ 28.2
True
This inequality is shown in the picture.
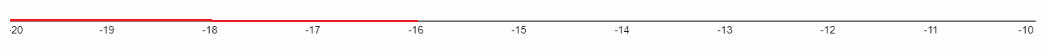
y ≤ -16
Question 17.
-3.6 ≥ -0.3a + 1.2
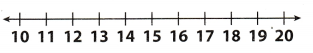
Answer:
Subtract 1.2 from boths sides.
-3.6 – 1.2 ≥ -0.3a + 1.2 – 1.2
-4.8 ≥ -0.3a Divide both sides by (-0.3).
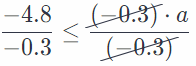Reverse the direction of inequality, due to the division by a negative number.
16 ≤ a
a ≥ 16
Check the solution for a ≥ 16. For example, a = 18.
-3.6 ⩼ (-0.3) . (18) + 1.2
-3.6 ⩼ -5.4 + 1.2
-3.6 ⩼ -4.2
True
This inequality is shown in the picture.
a ≥ 16
Question 18.
What If? The perimeter of a rectangle is at most 80 inches. The length of the rectangle is 25 inches. The inequality 80 – 2w ≥ 50 can be used to find w, the width of the rectangle in inches. Solve the inequality and interpret the solution. How will the solution change if the width must be at least 10 inches and a whole number?
Answer:
Subtract 80 from both sides.
-80 + 80 – 2 . w ≥ -80 + 50 Multiply both sides by (-2).
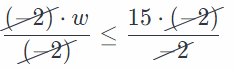Reverse the direction of inequality, due to the multiplication by a negative number.
The width is not greater than 15 inches.
If the width must be at least 10 inches and the whole number, the solution set is {10, 11, 12, 13, 14, 15}.
w ≤ 15 inches
Question 19.
Interpret the Answer Grace earns $7 for each car she washes. She always saves $25 of her weekly earnings. This week, she wants to have at least $65 in spending money. How many cars must she wash? Write and solve an inequality to represent this situation. Interpret the solution in context.
Answer:
Sum $25 Grace saves every week, and $7 . x. where x represents the number of cars she must wash, and that sum should be at least $65.
$25 + $7 . x ≥ $65 Subtract $25 from both sides.
-$25 + $25 + $7 . x ≥ -$25 + $65
$7 . x ≥ $40 Divide b0th sides by $7.
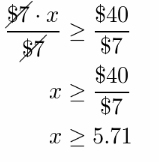
She can not wash 5.71 cars. so we have to take the next whole number.
Because of that, she must wash at least 6 cars to meet her goal. Proof:
$25 + $7 . 6 ⩼ $65
$25 + $42 ⩼ $65
$66 ⩼ $65
True
x ≥ 6
Texas Go Math Grade 7 Lesson 8.4 H.O.T. Focus On Higher Order Thinking Answer Key
Question 20.
Critical Thinking Is there any value of x with the property that x < x – 1? Explain your reasoning. Answer: No, there is not. If we decrease any number by 1, the obtained number can not be greater than himself. For example, let x be 5. 5 ⩻ 5 – 1 5 ⩻ 4 Not true. Not, there is not. Question 21. Analyze Relationships A compound inequality consists of two simple inequalities joined by the word “and” or “or.” Graph the solution sets of each of these compound inequalities. a. x > 2 and x < 7
Answer:
x > 2 and x < 7
b. x < 2 or x > 7
Answer:
x < 2 or x > 7
c. Describe the solution set of the compound inequality x < 2 and x > 7.
Answer:
The solution set is intersection of sets where x is greater than 2 and less than 7, x ε (2, 7).
d. Describe the solution set of the compound inequality x > 2 or x < 7.
Answer:
The solution set is union of sets where x is less than 2 and greater than 7, x ε (-∞, 2) ∪ (7, ∞).
Question 22.
Communicate Mathematical Ideas Joseph used the problem-solving strategy Work Backward to solve the inequality 2n+ 5 < 13. Shawnee solved the inequality using the algebraic method you used in this lesson. Compare the two methods.
Answer:
Working backward consists of mentally performing the following operations: Subtract 5 from 13 to obtain 8 and
dividing by 2 gives us that n must be less than 4.
Let’s perform the algebraic operations:
2n + 5 < 13 Write the inequality
2n + 5 – 5 < 13 – 5 Subtract 5 from both sides
2n < 8 Simplify
\(\frac{2 n}{2}\) < \(\frac{8}{2}\) Divide both sides by 2
n < 4 Simplify
The two methods are basically the same. Working backward consists of mostly working mentally, while algebraic method is mostly written, but operations performed are the same.
The two methods are basically the same. Backward method is working mentally while algebraic method is written solution.