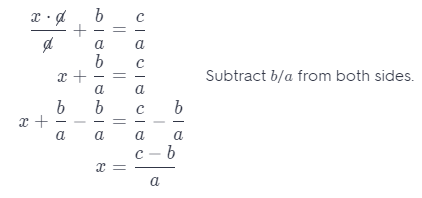Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 8.2 Answer Key Solving Two-Step Equations.
Texas Go Math Grade 7 Lesson 8.2 Answer Key Solving Two-Step Equations
Your Turn
Use algebra tiles to model and solve each equation.
Question 1.
2x + 5 = -11 __________
Answer:

First step
On the left side put 2 positive variables and 5 +1 tiles. On the right side put 11 + 1 tiles.
Second step
Remove 5 + 1 tiles from each side of the mat.
Third step
Divide each side into 2 groups.
The solution is x = 3
Question 2.
3n – 1 = 8 ___________
Answer:
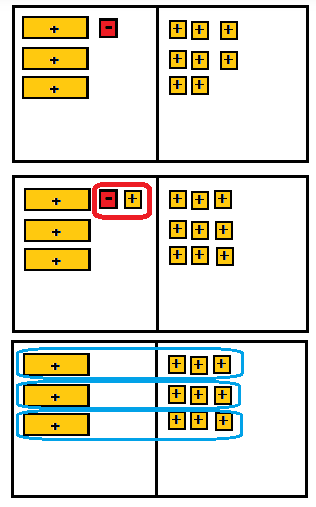
First step
On the left side put 3 positive variables and 1 – 1 tiles. On the right side put 8 + 1 tiles.
Second step
Add 1 + 1 tiles to each side of the mat.
The sum of the +1 and 1 tiles is 0.
Third step
Divide each side into 3 groups.
The solution is n = 3.
Question 3.
2a – 3 = -5 __________
Answer:
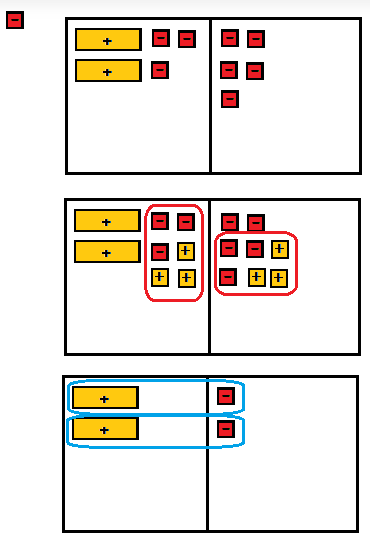
First step
On the left side put 2 positive variables and 3 – 1 tiles. On the right side put 5 – 1 tiles.
Second step
Add 3 + 1 tiles to each side of the mat.
The sum of the +1 and 1 tiles is 0.
Third step
Divide each side into 2 groups.
The solution is a = -1.
Question 4.
-4y + 2 = -2 ___________
Answer:
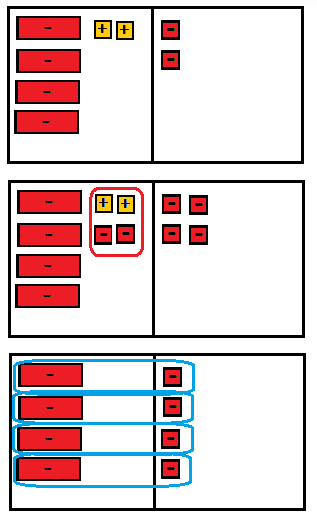
First step
On the left side put 4 negative variable and 2 + 1 tiles. On the right side put 2 – 1 tiles.
Second step
Remove 2 + 1 tiles from each side of the mat.
The sum of the +1 and -1 tiles is 0.
Third step
Divide each side into 4 groups.
The solution is -y = -4, hence y = 4.
Example 2
Tony carried 5 identical baseball bats to a ball game inside a carrying case weighing 12 ounces. The combined weight of the bats and the case was 162 ounces. How much did each bat weigh? Graph the solution on a number line.

Reflect
Question 5.
Analyze Relationships Describe how you could find the weight of one baseball bat using only arithmetic. Compare your method with the one used in Example 2.
Answer:
Using the arithmetic method, first subtract the weight of the case from the combined weight of the bats and case.
162 – 12 = 150
Then, divide the result by 5, since there are 5 identical bats.
150 ÷ 5 = 30
Each bat weighs 30 ounces. The two methods gave the same result. For some, it would be easier to use arithmetic and for some using an equation is easier. It will always depend on who is answering the problem which method they would prefer.
Your Turn
Write and solve an equation that represents the situation. Graph the solution on the number line.
Question 6.
Maureen wants to buy a $198 camera. She has $30 and plans to save $12 each week. In how many weeks will she be able to buy the camera?

Answer:
Sum $30 that Maureen has, and $12x, where x represents the number of weeks, to get the amount. of money she needs for the camera.
$30 + $12 ∙ x = $198 Subtract $30 from both sides.
-$30 + $30 + $12 ∙ x = $30 + $198
$12∙ x = $168 Divide both sides by $12.
\(\frac{\$ 12 \cdot x}{\$ 12}=\frac{14 \cdot \$ 12}{\$ 12}\)
x = 14
![]()
$30 + $12 ∙ x = $198
Question 7.
A rectangular picture frame has a perimeter of 58 inches. The height of the frame is 18 inches. What is the width of the frame?

Answer:
A perimeter of a rectanguLar is equal the sum 2 × height and 2 × width. Let x be the width of the frame.
18 + 2 ∙ x = 58 Subtract 18 from both sides.
-18 + 18 + 2 ∙ x = -18 + 58
2 ∙ x = 40 Divide both sides by 2.
\(\frac{2 \cdot x}{2}=\frac{20 \cdot 2}{2}\)
x = 20 inches

18 + 2 ∙ x = 58
Determine which, if any, of the given values is a solution.
Question 8.
3k + 15 = 66
k = -7; k = 17; k = 27
Answer:
Substitute 7 for k in the given equation.
k = 7
3 ∙ (-7) + 15 ≟ 66
-21 + 15 ≟66
-6 ≟ 66
Not true.
Substitute 17 for k in the given equation.
k = 17
3 ∙ (17) + 15 ≟ 66
51 + 15 ≟ 66
66 ≟ 66
True.
Substitute 27 for k in the given equation.
k = 27
3 ∙ (27) + 15 ≟ 66
81 + 15 ≟ 66
96 ≟ 66
Not True.
Question 9.
\(\frac{p}{2}\) – 5 = 7
p = -72; p = 18; p = 108
Answer:
Substitute 72 for p in the given equation.
p = 72
\(\frac{-72}{9}\) – 5 ≟ 7 Multiply by 9 both sides
\(\frac{-72 \cdot 9}{9}\) – 5 ∙ 9 ≟ 7 ∙ 9
-72 – 45 ≟ 63
-117 ≟ 63
Not true.
Substitute 18 for p in the given equation.
p = 18
\(\frac{18}{9}\) – 5 ≟ 7 Multiply by 9 both sides
\(\frac{18 \cdot 9}{9}\) – 5 ∙ 9 ≟ 7 ∙ 9
18 – 45 ≟ 63
-27 ≟ 63
Not true.
Substitute 108 for p in the given equation.
p = 108
\(\frac{108}{9}\) – 5 ≟ 7 Multiply by 9 both sides
\(\frac{108 \cdot 9}{9}\) – 5 ∙ 9 ≟ 7 ∙ 9
108 – 45 ≟ 63
63 ≟ 63
True.
Texas Go Math Grade 7 Lesson 8.2 Guided Practice Answer Key
The equation 2x + 1 = 9 is modeled below. (Example 1)
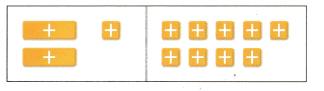
Question 1.
To solve the equation with algebra tiles, first remove. ____________.
Then divide each side into ______________
Answer:
- first remove +1 tile from each side
- then divide each side into 2 equal groups
Question 2.
The solution is x = ________________
Answer:
The solution is x = 4
Solve each equation. Then graph the solution on the number line. (Example 2)
Question 3.
8m – 15 = 41
m = ___________

Answer:
Add 15 to both sides.
8m – 15 + 15 = 41 + 15
8m = 56 Divide both sides by 8.
\(\frac{8 \cdot m}{8}=\frac{56}{8}\)
m = 7

Question 4.
\(\frac{k}{3}\) + 21 = 27
k = ____________

Answer:
Subtract 21 from both sides.
\(\frac{k}{3}\) + 21 – 21 = 27 – 21
\(\frac{k}{3}\) = 6 Multiply both sides by 3.
3 ∙ \(\frac{k}{3}\) = 3 ∙ 6
k = 18
Determine which, if any, of the given values is a solution. (Example 3)
Question 5.
9p – 18 = 27
p = 3; p = 5; p = 7
Answer:
Substitute 3 for p in the given equation.
p = 3
9 ∙ (3) – 18 ≟ 27
27 – 18 ≟ 27
9 ≟ 27
Not true.
Substitute 5 for p in the given equation.
p = 5
9 ∙ (5) – 18 ≟ 27
45 – 18 ≟ 27
27 ≟ 27
True.
Substitute 7 for p in the given equation.
p = 7
9 ∙ (7) – 18 ≟ 27
63 – 18 ≟ 27
45 ≟ 27
Not true.
Question 6.
\(\frac{a}{-2}\) – 5 = 0
a = -10; a = 0; a = 10
Answer:
Substitute 10 for a in the given equation
a = -10
\(\frac{-10}{-2}\) – 5 ≟ 0
\(\frac{-10 \cdot(-2)}{-2}\) – 5 ∙ (-2) ≟ 0 ∙ (-2) Multiply both sides by (-2)
– 10 + 10 ≟ 0
0 ≟ 0
True.
Substitute 0 for a in the given equation
a = 0
\(\frac{0}{-2}\) – 5 ≟ 0
0 – 5 ≟ 0
-5 ≟ 0
Not true.
Substitute 10 for a in the given equation
a = -10
\(\frac{10}{-2}\) – 5 ≟ 0
\(\frac{10 \cdot(-2)}{-2}\) – 5 ∙ (-2) ≟ 0 ∙ (-2) Multiply both sides by (-2)
10 + 10 ≟ 0
20 ≟ 0
Not true.
Essential Question Check-In
Question 7.
How can you decide which operations to use to solve a two-step equation?
Answer:
If we have variable multiplied by some number, we divide both sides of the equation by that number.
If we have variable divided by some number, we multiply both sides of the equation by that number.
If some number is added to variable, we subtract that number from both sides of the equation.
If some number is subtracted from variable, we add that number to the both sides of the equation.
Texas Go Math Grade 7 Lesson 8.2 Independent Practice Answer Key
Solve.
Question 8.
9s + 3 = 57
Answer:
Subtract 3 from both sides.
9 ∙ s + 3 – 3 = 57 – 3
9 ∙ s = 54 Divide both sides by 9.
\(\frac{s \cdot 9}{9}=\frac{6 \cdot 9}{9}\)
s = 6
Question 9.
4d + 6 = 42
Answer:
Subtract 6 from both sides.
4 ∙ d + 6 – 6 = 42 – 6
4 ∙ d = 36 Divide both sides by 4.
\(\frac{d \cdot 4}{4}=\frac{9 \cdot 4}{4}\)
d = 9
Question 10.
-3y + 12 = -48
Answer:
Subtract 12 from both sides.
-3 ∙ y + 12 – 12 = 48 – 12
-3 ∙ y = 60 Divide both sides by 4.
\(\frac{y \cdot(-3)}{3}=\frac{20 \cdot(-3)}{3}\)
y = 20
Question 11.
\(\frac{k}{2}\) + 9 = 30
Answer:
Multiply both sides by 2.
\(\frac{k \cdot 2}{2}\) + 9 ∙ 2 = 30 ∙ 2
k + 18 = 60 Subtract 18 from both sides
k + 18 – 18 = 60 – 18
k = 42
Question 12.
\(\frac{g}{3}\) – 7 = 15
Answer:
Multiply both sides by 3.
\(\frac{g \cdot 3}{3}\) + 7 ∙ 3 = 15 ∙ 3
g – 21 = 45 Subtract 21 from both sides
g – 21 + 21 = 45 + 21
g = 66
Question 13.
\(\frac{z}{5}\) + 3 = -35
Answer:
Multiply both sides by 5.
\(\frac{z \cdot 5}{5}\) + 3 ∙ 5 = (-35) ∙ 2
z + 15 = -105 Subtract 15 from both sides
z + 15 – 15 = -105 – 15
k = -120
Question 14.
-9h – 15 = 93
Answer:
Add 15 to both sides.
-9 ∙ h – 15 + 15 = 93 + 15
-9 ∙ h = 108 Divide both sides by (-9)
\(\frac{h \cdot(-9)}{-9}=\frac{(-12) \cdot(-9)}{-9}\)
h = -12
Question 15.
24 + \(\frac{n}{4}\) = 10
Answer:
Multiply both sides by 4.
24 ∙ 4 + \(\frac{n \cdot 4}{4}\) = 10 ∙ 4
96 + n = 40 Subtract 96 from both sides.
-96 + 96 + n = -96 + 40
n = – 56
Question 16.
-17 + \(\frac{b}{8}\) = 13
Answer:
MuLtiply both sides by 8.
(-17) ∙ 8 + \(\frac{b \cdot 8}{8}\) = 13 ∙ 8
-136 + b = 104 Add 136 to both sides.
136 – 136 + b = 136 + 104
b = 240
Question 17.
-5 = 9 + \(\frac{c}{4}\)
Answer:
Multiply both sides by 4.
(-5) ∙ 4 = 9 ∙ 4 + \(\frac{c \cdot 4}{4}\)
-20 = 36 + c Subtract 36 from both sides
-36 – 20 = -36 + 36 + c
-56 = c
c = -56
Question 18.
-3 + \(\frac{p}{7}\) = -5
Answer:
Multiply both sides by 7.
(-3) ∙ 7 + \(\frac{p \cdot 7}{7}\) = ( 5) ∙ 4
-21 + p = -35 Add 21 to both sides.
21 – 21 + p = 21 – 35
p = -14
Question 19.
46 =-6t – 8
Answer:
Divide by (-6) both sides

Question 20.
After making a deposit, Puja had $264 in her savings account. She noticed that if she added $26 to the amount originally in the account and doubled the sum, she would get the new amount. How much did she originally have in the account?
Answer:
Let x be the amount originally in the account.
If she added $26 to x and double it, she’ll get 264 in lier’s saves account.
Hence, the equation will be
(x + 26)2 = 264 Divide both sides by 2.
\(\frac{(x+26) 2}{2}=\frac{264}{2}\)
x + 26 = 132 Subtract 26 from both sides.
x + 26 – 26= 132 – 26
x = 106
She originally had 106 dollars in the account.
Question 21.
The current temperature in Smalltown is 20 °F. This is 6 degrees less than twice the temperature that it was six hours ago. What was the temperature in Smalltown six hours ago?
Answer:
Let x be the temperature in Smalltown six hours ago.
20° + 60° = 2 ∙ x
26° = 2 ∙ x Divide both sides by 2.
\(\frac{26^{\circ}}{2}=\frac{2 \cdot x}{2}\)
13° = x
x = 13°
Question 22.
Daphpe gave away 3 more than half of her apples. She gave away 17 apples in all. How many apples did Daphne have originally?.
Answer:
Multiply both sides by 2
3 ∙ 2 + \(\frac{x \cdot 2}{2}\) = 17 ∙ 2
6 + x = 34 Subtract 6 from both sides.
-6 + 6 + x = 6 + 34
x = 28
Question 23.
Artaud noticed that if he takes the opposite of his age and adds 40 he gets the number 28. How old is Artaud?
Answer:
Subtract 40 from both sides
-x + 40 – 40 = 28 – 40
-x = -12 Multiply both sides by (-1)
(-1) ∙ x = (-1) ∙ (-12)
x = 12
Question 24.
Sven has 11 more than twice as many customers as when he started selling newspapers. He now has 73 customers. How many did he have when he started?
Answer:
Subtract 11 from both sides
-11 + 11 + 2x = -11 + 73
2x = 62 Divide both sides by 2.
\(\frac{2 \cdot x}{2}=\frac{62}{2}\)
x = 31
Question 25.
Paula bought a ski jacket on sale for $6 less than half its original price. She paid $88 for the jacket. What was the original price?
Answer:
Multiply both sides by 2.
\(\frac{x \cdot 2}{2}\) – 6 ∙ 2 = 88 ∙ 2
x – 12 = 176 Add 12 to both sides
x – 12 + 12 = 176 + 12
x = 188
Question 26.
Michelle has a starting balance on a gift card for $300. She buys several dresses at $40 a piece. After her purchases she has $140 left on the gift card. How many dresses did she buy?
Answer:
Divide by (-40) both sides.

Use a calculator to solve each equation.
Question 27.
-5.5x + 0.56 = -1.64
Answer:
Subtract 0.56 from both sides.
-5.5 ∙ x + 0.56 – 0.56 = -1.64 – 0.56
-5.5 ∙ x = -2.2 Divide both sides by (-5.5).
\(\frac{(-5.5) \cdot x}{(-5.5)}=\frac{-2.2}{-5.5}\)
x = 0.4
Question 28.
-4.2x + 31.5 = -65.1
Answer:
Subtract 31.5 from both sides.
-4.2 x + 31.5 – 31.5 = -65, 1 – 31,5
-4.2 x = -96.6 Divide both sides by (-4.2).
\(\frac{(-4.2) \cdot x}{(-4.2)}=\frac{-96.6}{-4.2}\)
x = 23
Question 29.
\(\frac{k}{5.2}\) + 81.9 = 47.2
Answer:
Subtract 81.9 from both sides
\(\frac{k}{5.2}\) + 81.9 – 81.9 = 47.2 – 81.9
\(\frac{k}{5.2}\) = -34.7 Multiply both sides by 5.2
\(\frac{5 \cdot 2 \cdot k}{5.2}\) = (-34.7) ∙ 5.2
k = -180.44
Question 30.
Write a two-step equation involving multiplication and subtraction that has a solution of x = 7.
Answer:
First, we multiply x by 10, and then we subtract 20 from 10x. So, we have multiplication and subtraction in following equation.
10 ∙ x – 20 = 50
Question 31.
Write a two-step equation involving division and addition that has a solution of x = -25
Answer:
First, we divide x by 5, and then we add 20 to 5x. So, we have division and addition in following equation.
\(\frac{x}{5}\) + 20 = 15
Question 32.
Reason Abstractly The formula F = 1,8C + 32 allows you to find the Fahrenheit (F) temperature for a given Celsius (C) temperature. Solve the equation for C to produce a formula for finding the Celsius temperature for a given Fahrenheit temperature.
Answer:
Subtract 32 from both sides
F – 32 = 18C + 32 – 32
F – 32 = 18C Divide both sides by 18.
\(\frac{F}{18}\) – \(\frac{32}{18}\) = \(\frac{18 \cdot C}{18}\)
\(\frac{1}{18}\) ∙ F – 1.78 = C
0.55F – 1.78 = C
C = 0.55F – 1.78
Question 33.
Reason Abstractly The equation P = 2(l + w) can be used to find the perimeter P of a rectangle with length l and width w. Solve the equation for w to produce a formula for finding the width of a rectangle given its perimeter and length.
Answer:
Divide both sides by 2
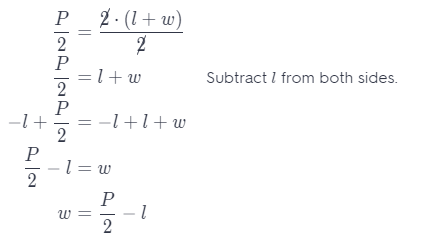
H.O.T. Focus on Higher Order Thinking
Question 34.
Critique Reasoning A student’s solution to the equation 3x + 2 = 15 is shown. Describe the error that the student made.
3x + 2 = 15 Divide both sides by 3.
x + 2 = 5 Subtract 2 from both sides,
x = 3
Answer:
When the student had divided both sides by 3, he didn’t divide number 2 on the left side.
Question 35.
Multiple Representations Explain how you could use the work backward problem-solving strategy to solve the equation \(\frac{x}{4}\) – 6 = 2.
Answer:
Translating the given equation to words, 6 was subtracted to a number divided by 4 and the result will be 2. Using the backward problem-solving strategy, add 6 to 2, which is 8 then multiply it by 4 and the result is 32.
Question 36.
Reason Abstractly Solve the equation ax + b = c for x.
Answer:
Divide both sides by a.