Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 5.2 Answer Key Experimental Probability of Simple Events.
Texas Go Math Grade 7 Lesson 5.2 Answer Key Experimental Probability of Simple Events
Texas Go Math Grade 7 Lesson 5.2 Explore Activity Answer Key
Finding Experimental Probability
You can toss a paper cup to demonstrate experimental probability.
A. Consider tossing a paper cup. Fill in the Outcome column of the table with the three different ways the cup could land.
B. Toss a paper cup twenty times. Record your observations in the table.
Reflect
Question 1.
Which outcome do you think is most likely?
Answer:
The most likely outcome is the one that happened most often.
Question 2.
Describe the three outcomes using the words likely and unlikely.
Answer:
Outcome – open-end up in experiment is unlikely;
Outcome – open-end down is unlikely;
Outcome – its side is likely.
Question 3.
Use the number of times each event occurred to calculate the probability of each event.
Answer:
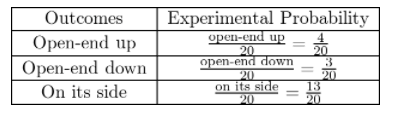
P (open-end up) = \(\frac{4}{20}\)
P (open-end down) = \(\frac{4}{20}\)
P (on its side) = \(\frac{4}{20}\)
Question 4.
What do you think would happen if you performed more trials?
Answer:
Probability will slowly approximate.
Question 5.
What is the sum of the three probabilities in the table?
Answer:
The sum of the three probabiLities is:
\(\frac{3}{20}\) + \(\frac{4}{20}\) + \(\frac{13}{20}\) = 1
Example 1
Martin has a bag of marbles. He removed one marble, recorded the color and then placed it back in the bag. He repeated this process several times and recorded his results in the table. Find the probability of drawing each color. Write your answers in simplest form.
A. Number of trials = 50
B. Complete the table of experimental probabilities. Write each answer as a fraction in simplest form.
Reflect
Question 6.
What are two different ways you could find the experimental probability of the event that you do not draw a red marble?
Answer:
P(red) = \(\frac{6}{25}\)
P(blue) = \(\frac{1}{5}\)
P(green) = \(\frac{3}{10}\)
P(yellow) = \(\frac{13}{50}\)
First Way
The sum of the probabiLities of an event and ¡ts compIement equals 1
P(event) + P(complement) = 1
P(red) + P(not red) = 1 Substitute \(\frac{6}{25}\) for P(red).
\(\frac{6}{25}\) + P(not red) = 1 Subtract \(\frac{6}{25}\) from both sides.
P(not red) = 1 – \(\frac{6}{25}\)
P(not red) = \(\frac{19}{25}\)
The probability of not drawing a red marble is \(\frac{19}{25}\).
Second Way
The probability of not drawing a red marble equals the probability of drawing a marble of any other color.
Since we have 3 other colors, the probability of drawing a marble of any other color is the sum of the probabilities of drawing each one of them.
P(not red) = P(blue) + P(green) + P(yellow) Substitute \(\frac{1}{5}\) for P(blue), \(\frac{3}{10}\) for P(green), and \(\frac{13}{50}\).
P(not red) = \(\frac{1}{5}+\frac{3}{10}+\frac{13}{50}\)
P(not red) = \(\frac{1 \cdot 10+3 \cdot 5+13}{50}\)
P(not red) = \(\frac{38}{50}\)
P(not red) = \(\frac{19 \cdot 2}{25 \cdot 2}\)
P(not red) = \(\frac{19}{25}\)
The probability of not drawing a red marble is \(\frac{19}{25}\).
Your Turn
Question 7.
A spinner has three unequal sections: red, yellow, and blue, The table shows the results of Nolan’s spins. Find the experimental probability of landing on each color. Write your answers in simplest form.
Answer:
The number of trials is the sum of frequencies.
Total number of trials is = 10 + 14 + 6 = 30
P(red color) = 
Substitute 10 for frequency of the event, and 30 for total number of trials.
P(red color) = \(\frac{10}{30}\)
P(red color) = \(\frac{1 \cdot 10}{3 \cdot 10}\)
P(red color) = \(\frac{1}{3}\)
P(yellow color) = Substitute 14 for frequency of the event, and 30 for total number of trials.
P(yellow color) = \(\frac{14}{30}\)
P(yellow color) = \(\frac{7 \cdot 2}{15 \cdot 2}\)
P(yellow color) = \(\frac{7}{15}\)
P(blue color) = Substitute 6 for frequency of the event, and 30 for total number of trials.
P(yellow color) = \(\frac{6}{30}\)
P(yellow color) = \(\frac{1 \cdot 6}{5 \cdot 6}\)
P(yellow color) = \(\frac{1}{5}\)
Question 8.
A toy machine has equal numbers of red, white, and blue rubber balls. Ross wonders which color ball will come out of the machine next. Describe how you can use a standard number cube to model this situation. Then use a simulation to predict the color of the next ball.
Answer:
The standard cube has six sides marked with numbers 1, 2, 3, 4, 5, 6. If the numbers 1 and 2 come up, the red ball is released, 3 or 4 comes out white and 4 or 5 turns out blue.
Let’s throw the cube 10 times and we’ll make numbers:
6, 5, 5, 4, 5, 2, 3, 1, 2, 4
It means it will. come out 4 blue, 3 white and 3 red balls.
Therefore, you can predict that blue ball has most of chance to come out.
Texas Go Math Grade 7 Lesson 5.2 Guided Practice Answer Key
Question 1.
Toss a coin at least 20 times. (Explore Activity and Example 1)
a. Record the results in the table.
Answer:
P (flip a head) = \(\frac{2}{5}\)
P (flip a tails) = \(\frac{3}{5}\)
b. What do you think would happen if you performed more trials?
Answer:
Probabilities will be the same.
Question 2.
Rachel’s free-throw average for basketball is 60%. Describe how you can use 10 index cards to model this situation. Then use a simulation to predict how many times in the next 50 tries Rachel will make a free throw. (Example 2).
Answer:
Let the cards be marked with numbers from 1 to 10. Let numbers 1, 2, 3, 4, 5, 6 represent that free-throw is on average, while numbers 7, 8, 9, lO, and the free-throw was beLow the average.
Let’s draw one card, we’ll record the number that we have and return it again Let’s repeat this 50 times
4, 7, 5, 6, 8, 5, 4, 2, 1, 1, 1, 9, 7, 10, 10, 6, 3, 4, 4, 5, 7, 8, 2, 1, 5, 8, 4, 10, 2, 2, 6, 7, 7, 5, 4, 1, 3, 2, 2, 2, 6, 7, 10, 3, 5, 9, 7, 4, 4, 1
Reachel will make a free throw 34 times.
Essential Question Check-In
Question 3.
Essential Question Follow Up How do you find the experimental probability of a simple event?
Answer:
Experimental probability is a value of number of time the event occurs divided by total number of trials.
Texas Go Math Grade 7 Lesson 5.2 Independent Practice Answer Key
Question 4.
Dree rolls a strike in 6 out of the 10 frames of bowling. What is the experimental probability that Dree will roll a strike in the first frame of the next game? Explain why a number cube would not be a good way to simulate this situation.
Answer:
P (roll a strike) = 
The experimental probability that Dree will roll a strike in first frame of next game is \(\frac{3}{5}\).
The cube is not good for presenting this situation because we have the probability of achieving the goal of \(\frac{3}{5}\), so three numbers would be marked as winnings, two that were not, and with the remaining number would have no meaning.
Question 5.
To play a game, you spin a spinner like the one shown. You win if the arrow lands in one of the areas marked “WIN”. Lee played this game many times and recorded her results. She won 8 times and lost 40 times. Use Lee’s data to explain how to find the experimental probability of winning this game.
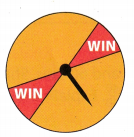
Answer:
P (lend on “WIN”) = \(\frac{1}{6}\)
Question 6.
Critique Reasoning A meteorologist reports an 80% chance of precipitation. Is this an example of experimental probability, written as a percent? Explain your reasoning.
Answer:
80% = \(\frac{80}{100}\) = \(\frac{4}{5}\)
This is the experimental probability, because when we translate into a fraction, it actually means that 4 out of 5 days will be percipitation.
Question 7.
The names of the students in Mr. Hayes’ math class are written on the board. Mr. Hayes writes each name on an index card and shuffles the cards. Each day he randomly draws a card, and the chosen student explains a math problem at the board. What is the probability that Ryan is chosen today? What is the probability that Ryan is not chosen today?
Answer:
P (Ryan is chosen) = \(\frac{1}{20}\)
P (Ryan is not chosen) = \(\frac{19}{20}\)
Question 8.
Mica and Joan are on the same softball team. Mica got 8 hits out of 48 times at bat, while Joan got 12 hits out of 40 times at bat. Who do you think is more likely to get a hit her next time at bat? Explain.
Answer:
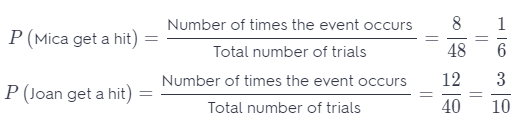
Is more likely that Joan get a hit because \(\frac{1}{6}\) < \(\frac{3}{10}\).
Question 9.
Make a Prediction In tennis, Gabby serves an ace, a ball that can’t be returned, 4 out of the 10 times she serves. What is the experimental probability that Gabby will serve an ace on the first serve of the next game? Make a prediction about how many aces Gabby will make on her next 40 serves. Justify your reasoning.
Answer:
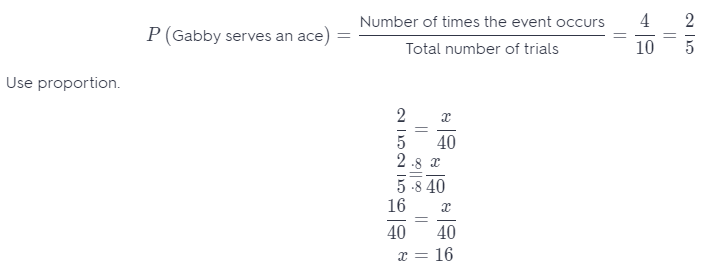
The probability that Gabby will serve an ace is \(\frac{2}{5}\).
You can predict that she will serve an ace about 16 times out of 40.
H.O.T. Focus on Higher Order Thinking
Question 10.
Represent Real-World Problems Patricia finds that the experimental probability of her dog wanting to go outside between 4 p.m. and 5 p.m. is \(\frac{7}{12}\) About what percent of the time does her dog not want to go out between 4 p.m. and 5 p.m.?
Answer:
P (dog wanting to go outside) = \(\frac{7}{12}\)
P (dog not want to go outside) = 1 – P (dog wanting to go outside) = 1 – \(\frac{7}{12}\) = \(\frac{12}{12}\) – \(\frac{7}{12}\) = \(\frac{5}{12}\)
Use proportion.
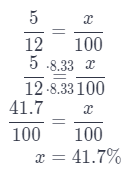
About 41.7 % her dog not want to go out between 4 p.m. and 5 p.m.
Question 11.
Critique Reasoning Talia tossed a penny many times; she got 40 heads and 60 tails. She said the experimental probability of getting heads was \(\frac{40}{60}\). Explain the error and correct the experimental probability.
Answer:
She actually tossed the coin 100 times and out of 100 she got 40 heads and 60 tails.
P (getting heads) = 
P (getting heads) = \(\frac{2}{5}\)
Question 12.
Communicate Mathematical Ideas A high school has 438 students, with about the same number of males as females. Describe a simulation to predict how many of the first 50 students who leave school at the end of the day are female.
Answer:
P (student is a female) = 
Have 25 red and 25 blue balls in the basket. If we choose a red ball, a female student comes out, otherwise a male student comes out.
Question 13.
Critical Thinking For a scavenger hunt, Chessa put one coin in each of 10 small boxes. Four coins are quarters, 4 are dimes, and 2 are nickels. How could you simulate choosing one box at random? What problem would there be if you planned to put these coins in your pocket and pick one?
Answer:
In the box are 10 balls, 4 blue, 4 white and 2 green. We choose randomly one ball If the ball is blue, we select one of the boxes in which the dimes are, if the ball is white, we select one of the boxes with quarter and if the ball is green we select one of the boxes with nickle.
If you put all the coins in your pocket then the probability will be equal for each coin.