Texas Go Math Grade 6 Unit 4 Study Guide Review Answer Key

Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Unit 4 Study Guide Review Answer Key.

Texas Go Math Grade 6 Unit 4 Study Guide Review Answer Key

Module 10 Generating Equivalent Numerical Expressions

Essential Question
How can you generate equivalent numerical expressions and use them to solve real-world problems?

Exercises

Use exponents to write each expression. (Lesson 10.1)

Question 1.
3.6 × 3.6 ______
Answer:
Solution to this example is given below
3.6 × 3.6
Find the base, or the numbers being multiplied. The base is 3.6
Find the exponents by counting the number of 3.6s being multiplied
The exponents is 2 (Final solution)

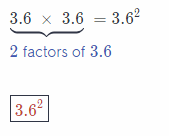
Question 2.
9 × 9 × 9 × 9 ______
Answer:
Solution to this example is given below
9 × 9 × 9 × 9
Find the base, or the numbers being multiplied. The base is 9
Find the exponents by counting the number of 9s being multiplied
The exponents is 4 Final solution

Question 3.
\(\frac{4}{5}\) × \(\frac{4}{5}\) × \(\frac{4}{5}\)
Answer:

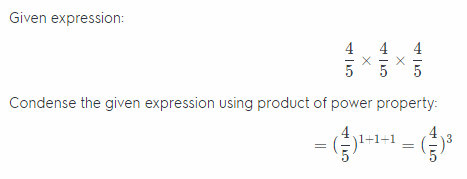
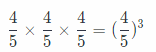
Find the value of each power. (Lesson 10.1)

Question 4.
12° ____
Answer:
Solution to this example is given below
12°
Identify the base and the exponents
The base is 12 and the exponents is 0.
Evaluate: 12° = 1 (Any power raised to exponent 0 is always equal to 1)
1 (Final solution)

Question 5.
13² ______
Answer:
Solution to this example is given below
13²
Identify the base and the exponents
The base is 13 and the exponents is 2. (Final solution)
Evaluate: 13² = 13 × 13 = 169
169

Question 6.
\(\left(\frac{2}{7}\right)^{3}\) ______
Answer:

Write the prime factorization of each number. (Lesson 10.2)

Question 7.
75 ____
Answer:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 75 are 3, 5 and 5.
The prime factorization of 75 is: (Final solution)
75 = 3 × 5 × 5 or 3 × 5²
3 × 5²

Question 8.
29 ____
Answer:
Given number: 29

Factorize the given number using its prime factors, therefore:
29 = 29
Prime factor of 29 is 29. This implies that 29 is a prime number

Prime factor of 29 is 29.

Question 9.
168 ______
Answer:

Question 10.
Eduardo is building a sandbox that has an area of 84 square feet. What are the possible whole number measurements for the length and width of the sandbox? (Lesson 10.2)
Answer:
Given number:
84

Write the given number as a product of its factors, therefore:
84 = 2 × 42
84 = 3 × 28
84 = 4 × 21
84 = 6 × 14
84 = 7 × 12
The required sandbox can have the dimensions of 2 by 42, 3 by 28, 4 by 21, 6 by 14 and 7 by 12.

Question 11.
2 × 5² – (4 + 1) ____
Answer:
Solution to this example is given below
2 × 5² – (4 + 1)
2 × 5² – (4 + 1) = 2 × 25 – (4 + 1) Evaluate 5².
= 2 × 25 – 5 Perform operations inside parentheses.
= 50 5 Multiply.
= 45 Subtract.
45 (Final solution)

Question 12.

Answer:

Module 11 Generating Equivalent Algebraic Expressions

Essential Question
How can you generate equivalent algebraic expressions and use them to solve real-world problems?

Exercises

Write each phrase as an algebraic expression. (Lesson 11.1)

Question 1.
x subtracted from 15 _____ 4
Answer:
Solution to this example is given below
x subtracted from 15. The operation is subtraction.
The algebraic expression is 15 – x
15 – x (Final solution)

Question 2.
12 divided by t ____
Answer:
Solution to this example is given below
12 divided by t. The operation is division.
The algebraic expression is \(\frac{12}{t}\)
\(\frac{12}{t}\) (Final solution)

Write a phrase for each algebraic expression. (Lesson 11.1)

Question 3.
8p ______
Answer:
Solution to this example is given below
8p The operation is Multiplication.
The product of 8 and p (Fina solution)
The product of 8 and p

Question 4.
s + 7 _____
Answer:
Solution to this example is given below
s + 7 The operation is Addition (Final solution)
The sum of s and 7

Evaluate each expression for the given value of the variable. (Lesson 11.2)

Question 5.
8z + 3; z = 8 ________
Answer:
Solution to this example is given below
8z + 3; z = 8
8(8) + 3 Substitute 8 for z
64 + 3 Multiply
67 Add
When z = 8, 8z + 3 = 67
Final solution

Question 6.
3(7 + x²);x = 2 ______
Answer:
Solution to this example is given below
3(7 + x²); x = 2
3(7 + 2²) Substitute 2 for x
3(7 + 4) Evaluate exponents
3(11) Add inside the parentheses
33 Multiply
When x = 2, 3(7 + x²) = 33
33 Final solution

Question 7.
s – 5t + s²; s = 4, t = -1 ____________
Answer:
Solution to this example is given below
s – 5t + s²; s = 4, and t = – 1
4 – 5(-1) + 4² Substitute 4 for s, and (-1) for t
4 – 5(-1) + 16 Evaluate exponents
4 + 5 + 16 Multiply
25 Add
When s = 4, and t = -1s – 5t + s² = 25
25 Final sotution

Question 8.
x – y³; x = -7, y = 3 ______
Answer:
Solution to this example is given below
x – y³; x = -7, and y = 3
-7 – 3³ Substitute (-7) for x, and 3 for y
– 7 – 27 Evaluate exponents
-34 Subtract
When x = -7, and y = 3, x – y³ = -34
-34 Final solution

Question 9.
The expression \(\frac{1}{2}\)(h)(b₁ + b₂) gives the area of a trapezoid, with b₁, and b₂ representing the two base lengths of a trapezoid and h representing the height. Find the area of a trapezoid with base lengths 4 in. and 6 in. and a height of 8 in. (Lesson 11.2) ________
Answer:
Solution to this example is given betow
\(\frac{1}{2}\)(h)(b₁ + b₂); h = 8, b₁ = 4, and b₂ = 6
\(\frac{1}{2}\)(8)(4 + 6) Substitute 8 for h, 4 for b₁, and 6 for b₂
4(4 + 6) Multiply
4(10) Add inside the parentheses
40 Multiply
When h = 8, b₁ = 4, and b₂ = \(\frac{1}{2}\)(h)(b₁ + b₂) = 40
Area of the given trapezoid is 40 square inches
40 Final solution

Determine if the expressions are equivalent. (Lesson 11.3)

Question 10.
7 + 7x; 7(x + \(\frac{1}{7}\))
Answer:
Given expression:
7(x + \(\frac{1}{7}\))
Apply distributive property to expand the parentheses:
= 7(x) + 7( \(\frac{1}{7}\))
Simplify:
= 7x + 1
Compare:
7x + 1 ≠ 7x + 7
The 2 expressions are not equivalent

Question 11.
2.5(3 + x); 2.5x + 7.5 ______
Answer:
Given expression:
2.5(3 + x)
Apply distributive property to expand the parentheses:
= 2.5(3) + 2.5(x)
Simplify:
= 7.5 + 2.5x
Compare:
7.5 + 2.5x = 7.5 + 2.5x
The 2 expressions are equivalent

Combine like terms. (Lesson 11.3)

Question 12.
3m – 6 + m² – 5m + 1 ____
Answer:
Combine like terms
3m – 6 + m² – 5m + 1
3m – 6 + m² – 5m + 1 = m² – 5m + 3m – 6 + 1 Commutative Property
= m² – 2m – 5 Distributive Property
3m – 6 + m² – 5m + 1 = m² – 2m – 5
m² – 2m – 5 Final Solution

Question 13.
7x + 4(2x – 6) _____
Answer:
Combine like terms
7x + 4(2x – 6)
7x + 4(2x – 6) = 7x + 8x – 24 Distributive Property
= 15x – 24 Add
7x + 4(2x – 6) = 15x – 24
15x – 24 Final Solution
15x – 24

Module 12 Equations and Relationships

Essential Question
How can you use equations and relationships to solve real-world problems?

Exercises

Determine whether the given value is a solution of the equation. (Lesson 12.1)

Question 1.
7x = 14; x = 3 _____
Answer:
Solution to this example is given below
7x = 14; x = 3
7(3) = 14 Substitute
21 ≠ 14 Multiply
3 is not a solution of 7x = 14.
x ≠ 3 Final solution

Question 2.
y + 13 = -4; y = -17 _____
Answer:

Write an equation to represent the situation. (Lesson 12.1)

Question 3.
Don has three times as much money as his brother, who has $25. ______
Answer:
Solution to this example is given below
\(\frac{x}{3}\) = 25
\(\frac{x}{3}\) × 3 = 25 × 3 Multiply both sides by3
x = 75 Simplify
Don has dollars
x = 75 Final solution

Question 4.
There are s students enrolled in Mr. Rodriguez’s class. There are 6 students absent and 18 students present today. _____
Answer:
The total number of student s is the sum of the students who are present and who are absent, so the equation becomes:
s = 18 + 6

Evaluate:
s = 24
24 students are enrolled in Mr. Rodriguez’s class.

Solve each equation. Check your answer. (Lessons 1 2.2,12.3)

Question 5.
p – 5 = 18
Answer:
Solution to this example is given below
p – 5 = 18
p – 5 + 5 = 18 + 5 Add both sides by 5
p = 23 Simplify
Check; 23 – 5 = 18 Substitute
18 = 18
p = 23 Final solution
p = 23

Question 6.
\(\frac{t}{4}\) = -12
Answer:
We wilt multiply both sides by 4 and get:
4(\(\frac{t}{4}\)) = 12(4)
t = 48
Now, we will substitute 48 for t into original equation to check our solution:
\(\frac{48}{4}\) = 12
So,
the solution is t = 48
t = 48

Question 7.
9q = 18.9 ____
Answer:
Solution to this example is given below
9q = 18.9

Question 8.
3.5 + x = 7
Answer:
Solution to this example is given below
3.5 + x = 7
3.5 + x – 3.5 = 7 – 3.5 Subtract both sides by 3.5
x = 3.5 Simplify
Check; 3.5 + 3.5 = 7 Substitute
7 = 7 Add on the left side
x = 3.5 Final solution

Question 9.
18 = x – 31 ____
Answer:
We will add 31 to both sides in order to isolate x:
49 = x
Now, we will check our solution substituting 49 for x into the original equation and get:
49 – 31 = 18
So, conclusion is that x = 49 is a solution.
x = 49

Question 10.
\(\frac{2}{7}\) = 2x _____
Answer:
Solution to this example is given below

Question 11.
Sonia used $12.50 to buy a new journal. She has $34.25 left in her savings account. How much money did Sonia have before she bought the journal? Write and solve an equation to solve the problem. (Lesson 12.2)
Answer:
Solution to this example is given below
x – 12.5 = 34.25
x – 12.5 + 12.5 = 34.25 + 12.5 Add both sides by 125
x = 46.75 Simplify
Check; 46.75 – 12.5 = 34.25 Substitute
34.25 = 31.25 Subtract on the left side
Sonia had 46.75 dollars before she bought the journal
x = 46.75 Final solution
x = 46.75

Question 12.
Tom read 132 pages in 4 days. He read the same number of pages each day. How many pages did he read each day? Write and solve an equation to solve the problem. (Lesson 12.3) _____
Answer:
Let x represent the number of pages Tom red each day. Using all informations in this task, we get the following equation:
4x = 132
In order to solve it, we need to divide both sides by 4 and get:
\(\frac{4 x}{4}\) = \(\frac{132}{4}\)
x = 33
So,
Tom red 33 pages each day.
33

Module 13 Inequalities and Relationships

Essential Question
How can you use inequalities and relationships to solve real-world problems?

Exercises

Write and graph an inequality to represent each situation (Lesson 13.1)

Question 1.
Orange Tech’s stock is worth less than $2.50 per share. ____

Answer:
Because here we have less than 2.50 and if x represent. Orange Techs stock, we get the following inequality:
x < 2.50

Question 2.
Tina got a haircut, and her hair is still at least 15 inches long. ____

Answer:
Draw a solid circle at 15 to show that 15 is a solution.
Shade the number tine to the right of 15 to show that numbers greater than 15 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as 16. Substitute 16 for x.
16 ≥ 15 : 16 greater than 15, so 16 is a solution
x ≥ 15 Final solution

Solve each inequality. Graph and check your solutions (Lessons 13.2, 13.3, 1 3.4)

Question 3.
q – 12 > 3 ____
Answer:
First we will add 12 to both sides and get:
q > 15
Now, we will graph the solution.

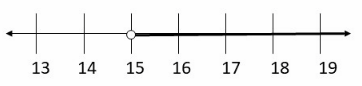
Now, we will check our solution substituting 16 for q into the original inequality and get:
16 – 12 > 3
4 > 3
so, the inequality is true.
q > 15

Question 4.
\(\frac{t}{4}\) ≤ -1 ____
Answer:
In order to solve the given inequality, we wilt multiply both sides by 4 and get:
\(\frac{t}{4}\) ≤ (-1)(4)
t ≤ -4
Now, we will graph the solution:

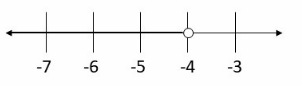
Next step ¡s to check the solution substituting some value from the shaded area on the number line.
For example, we Wilt substitute 8 for t into the original inequality:
\(\frac{-8}{4}\) ≤ -4
-2 ≤ -1
S0, the inequality is true.
t ≤ -4

Question 5.
9q > 10.8 ____
Answer:
In order to solve this inequality, we will divide both sides by 9 and get:
\(\frac{9q}{8}\) > \(\frac{10.8}{9}\)
q > 1.2
Now, we will graph the solution:

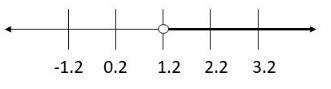
Next step is to check the solution substituting value from the shaded area on the number line.
For example, we will substitute 3.2 for q into the original inequality:
9 . 3.2 > 10.8
28.8 > 10.8
So, the Inequality is true
q > 1.2

Question 6.
87 ≤ 25 + x ____
Answer:
We wilt use Subtracting Property of Inequality, we will actually subtract 25 from both sides:
62 ≤ x
Now, we will graph the solution:

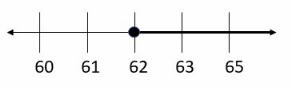
Next step is to check the solution substituting some value from the shaded area on the number line.
For example, we will substitute 65 for x into the original inequality:
87 ≤ 25 + 65
87 ≤ 90
So, the Inequality is true.
x ≥ 62

Question 7.
–\(\frac{4}{5}\) < 8 _____
Answer:
5 4
The first step is to multipLy both sides by –\(\frac{5}{4}\), which is reciprocal of –\(\frac{4}{5}\)
Because –\(\frac{4}{5}\) is a negative number, we need to reverse the inequality symbol in order to original inequality still be true.
So, we have the following:

Next step is to check the solution substituting some value from the shaded area on the number line.
For example, we will substitute 0 for x into the original inequality:
–\(\frac{4}{5}\) . 0 < 8
0 < 8 So, the Inequality is true. x > – 10

Question 8.
-4 ≥ -0.5x ____
Answer:
The first step is to divide both sides by -0.5. -0.5 is a negative number, we need to reverse the inequality symbol in order to original inequality still be true.
So, we have the following:

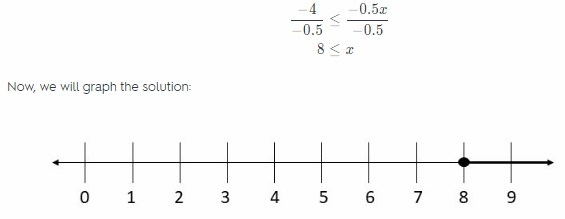
Next step is to check the solution substituting some value from the shaded area on the number line.
For example, we will substitute 10 for x into the original inequality:
-4 ≥ – 0.5 . 10
-4 ≥ -5
So, the Inequality is true.
x ≥ 8

Question 9.
Write a real-world comparison that can be described by x – 3 ≥ 11. (Lesson 13.2)
Answer:
A real-world comparison that can be described by given inequality could be:
If Tom gives to his brother 3 candies, he will left at least 11 candies more. How many candies Tom had?

Question 10.
Omar wants a rectangular vegetable garden. He only has enough space to make the garden 5 feet wide, and he wants the area of the garden to be more than 80 square feet. Write and solve an inequality to find the possible lengths of the garden. (Lesson 13.3)
Answer:
The area of this rectangular garden is a product of its width and length. Here, let x represent the possible length of the garden.
Using all pieces of information, we get the following inequality:
5x > 80
In order to solve this inequa1ity we need to divide both sides by 5 and get:
x > 16
So, the length of the garden can be greater than 16 feet.
x > 16

Module 14 Relationships in Two Variables

Essential Question
How can you use relationships in two variables to solve real-world problems?

Exercises

Graph and label each point on the coordinate plane. (Lesson 14.1)

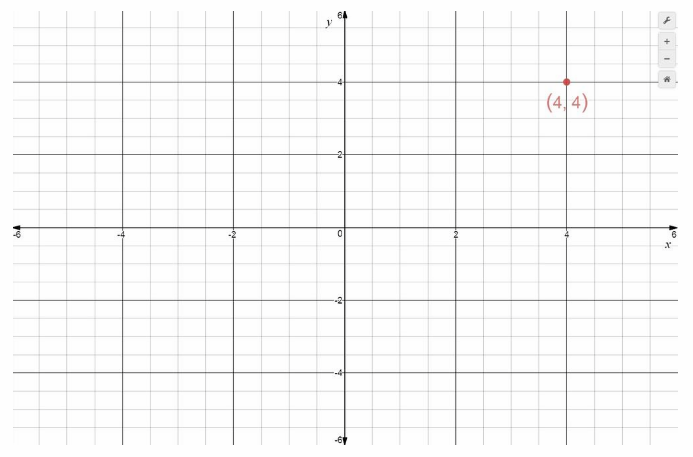
Question 1.
(4, 4)
Answer:
(4, 4 ) is located 4 units right of the origin, and 4 units up. It has x-coordinate 4 and y-coordinate 4, written (4, 4). It is located in Quadrant I.

Question 2.
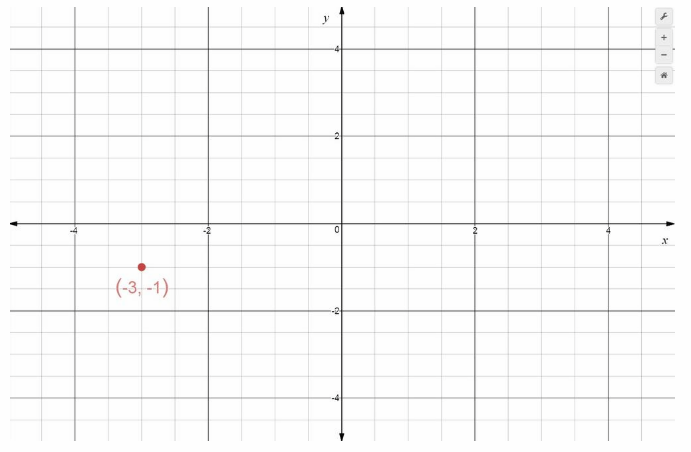
(-3, -1)
Answer:
(-3, -1) is located 3 units left of the origin, and 1 units down. It has x-coordinate -3 and y-coordinate -1, (-3, -1) is in Quadrant III

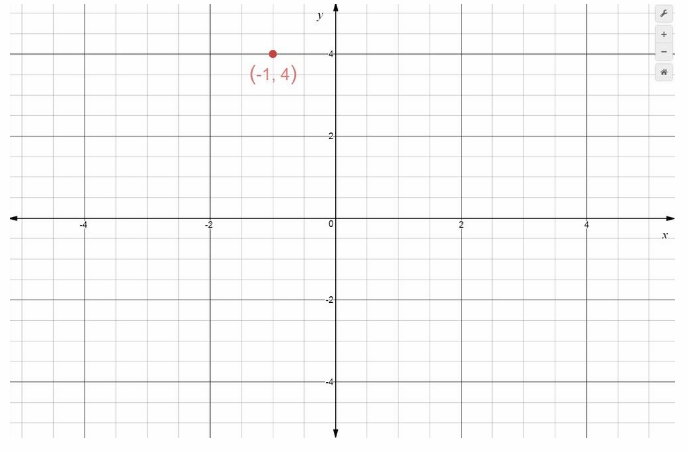
Question 3.
(-1, 4) ____
Answer:
(-1, 4 ) is located 1 units left of the origin, and 4 units up. It has x-coordinate -1 and y-coordinate 4.
(-1, 4) is in Quadrant II.

Use the graph to answer the questions. (Lesson 14.2)

Question 4.
What is the independent variable? __________________________
Answer:
What is the independent variable? Time in hours.
The independent variable is the variable taken on the x-axis of the graph It is time in hours here.
Time in hours.

Question 5.
What is the dependent variable? __________________ _________
Answer:
What is the dependent variable? Distance in miles.

The dependent variable is the variable taken on the y-axis of the graph. It is distance in miles here.
Distance in miles.

Question 6.
Describe the relationship between the independent variable and the dependent variable.
Answer:

Question 7.
Use the data on the table to write an equation to express y in terms of x. Then graph the equation. (Lessons 14.3, 14.4)

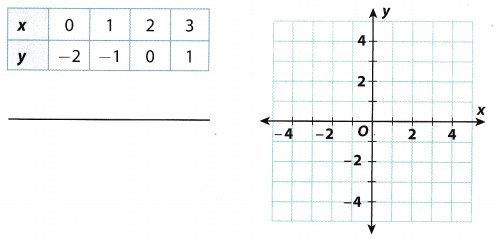
Answer:
Using the data in the table, we will try to find a relationship between x between x and y. Let x₁ be 0 and x₂ be 1.
So, y₁ will be -2 and y₂ will be -1. We will use the line through those two points and get:

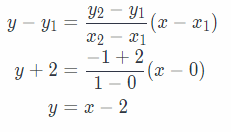
So, required equation is y = x – 2. Now, we will graph the solution.

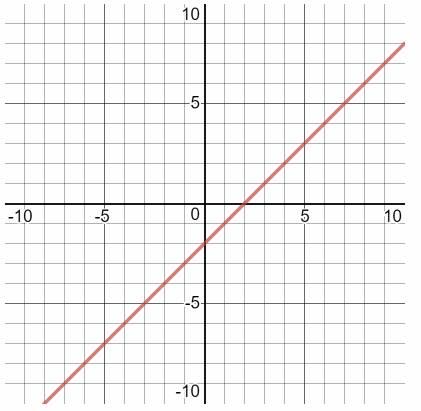
y = x – 2

Texas Go Math Grade 6 Unit 4 Performance Tasks Answer Key

Question 1.
Careers In Math Botanist Dr. Adama is a botanist. She measures the daily height of a particular variety of sunflower, Sunny Yellow, beginning when the sunflower is 60 days old. At 60 days, the height of the sunflower is 205 centimeters. Dr. Adama finds that the growth rate of this sunflower is 2 centimeters per day after the first 60 days.

a. Write an expression to represent the sunflower’s height d days after the 60th day.
Answer:
Let h represent the height of the sunflower using all pieces of information, we get the following equation:
h = 205 + 2d

b. How many days after the 60th day does it take for the sunflower to reach 235 centimeters? Show your work.
Answer:
We will substitute 235 for h in previous equation and solve it for d.
235 = 205 + 2d
30 = 2d
d = 15
So, after 15 days after the 60th day
sunflower will reach 235 centimeters.

c. Dr. Adama is studying a different variety of sunflower, Suntracker, which grows at a rate of 2.5 centimeters per day after the first 60 days. If this sunflower is 195 centimeters tall when it is 60 days old, write an expression to represent Suntracker’s height d days after the 60th day. Which sunflower will be taller 22 days after the 60th day? Explain how you found your answer.
Answer:
Let h represent height of the sunflower, using all informations, we get the following equation:
h = 195 + 2.5d
Now, we will substitute 22 for d into the previous equation and solve it for h.
h = 195 + 2.5 . 22 = 250
So, the sunflower will reach 2.50 centimeters 22 days after the 60th day in second case.
Now we wilt substitute 22 for d into equation form part a and solve it for h:
h = 205 – 2 . 22 = 249
We can notice that sunflower in trie second case, from this part c, wilt be taller.

Question 2.
Vernon practiced soccer 5\(\frac{3}{4}\) hours this week. He practiced 4\(\frac{1}{3}\) hours on weekdays and the rest over the weekend.

a. Write an equation that represents the situation. Define your variable.
Answer:
Let x represent a number of hours Vermon practiced during the work days in the week. We get the following equation:
x = 5\(\frac{3}{4}\) – 4\(\frac{1}{3}\)

b. What is the least common multiple of the denominators of 5\(\frac{3}{4}\) and 4\(\frac{1}{3}\)? Show your work.
Answer:
First we need to rewrite those mixed numbers as a fractions:
5\(\frac{3}{4}\) = \(\frac{23}{4}\)
4\(\frac{1}{3}\) = \(\frac{13}{3}\)
The denominators are 4, 3 and their the least common multiple is 12.

c. Solve the equation and interpret the solution. Show your work.
Answer:
Now, we will calculate z:

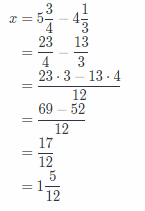
So, over the weekend, Vermon practiced 1\(\frac{5}{12}\) hour

Texas Go Math Grade 6 Unit 4 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
Which expression is equivalent to 2.3 × 2.3 × 2.3 × 2.3 × 2.3?
(A) 2.3 × 5
(B) 23⁵
(C) 2⁵ × 3⁵
(D) 2.3⁵
Answer:
(D) 2.3⁵

Explanation:
Solution to this example is given below
2.3 × 2.3 × 2.3 × 2.3 × 2.3
Find the base, or the numbers being multiplied. The base is 2.3
Find The exponents by counting the number of 2.3s being multiplied
The exponents is 5 (This option is correct answer)

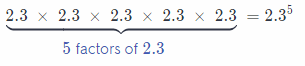
D

Question 2.
Which operation should you perform first when you simplify 63 – (2 + 54 × 6) ÷ 5?
(A) addition
(B) division
(C) multiplication
(D) subtraction
Answer:
(C) multiplication

Explanation:
Solution to this example is given below
63 – (2 + 54 × 6) ÷ 5 (This operation is correct answer)
63 – (2 + 54 × 6) ÷ 5 = 63 – (2 + 324) ÷ 5 Perform operations inside parentheses.
C

Question 3.
Sheena was organizing items in a scrapbook. She took 25 photos and divided them evenly among p pages. Which algebraic expression represents the number of photos on each page?
(A) p – 25
(B) 25 – p
(C) \(\frac{p}{25}\)
(D) \(\frac{25}{p}\)
Answer:
(D) \(\frac{25}{p}\)

Explanation:
Solution to this example is given below
25 divided p. The operation is division.
The algebraic expression is \(\frac{25}{p}\) (This option is correct answer)
D

Question 4.
The number line below represents which equation?

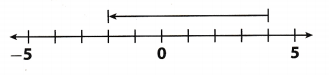
(A) -2 + 6 = 4
(B) -2 – 6 = 4
(C) 4 + 6 = -2
(D) 4 – 6 = -2
Answer:
(A) -2 + 6 = 4

Explanation:
Looking at this line below, we can conclude that the equation which represents this line is A.
-2 + 6 = 4
A

Question 5.
No more than 7 copies of a newspaper are left in the newspaper rack. Which inequality represents this situation? (A) n < 7 (B) n ≤ 7 (C) n > 7
(D) n ≥ 7
Answer:
(B) n ≤ 7

Explanation:
The words no more than indicate that the maximum number of copies on the rack were 7. so the inequality is: n ≤ 7
Option B

Question 6.
For which of the inequalities below is v = 4 a solution?
(A) v + 5 > 9
(B) v + 5 > 9
(C) v + 5 ≤ 8
(D) v + 5 < 8
Answer: (A) v + 5 > 9

Explanation:
Substitute v = 4 in each inequaLity and check for which inequality the inequality holds true, therefore:

A. 4 + 5 ≥ 9
Simplify:
9 ≥ 9
Inequality holds true.

B. 4 + 5 > 9
Simplify:
9 > 9
Inequality does not hold true.

C. 4 + 5 ≤ 8
Simplify:
9 ≤ 8
Inequality does not hold true.

D. 4 + 5 < 9
Simplify:
9 < 8
Inequality does not hold true.
Option A

Question 7.
Sarah has read aloud in class 3 more times than Joel. Sarah has read 9 times. Which equation represents this situation?
(A) j – 9 = 3
(B) 3j = 9
(C) j – 3 = 9
(D) j + 3 = 9
Answer:
(B) 3j = 9

Explanation:
Let the number of Joel’s reading turn be j, then Sarah’s turns are 3 × j = 9.
Option B.

Question 8.
The number line below represents the solution to which inequality?

(A) \(\frac{m}{4}\) > 1.1
(B) \(\frac{m}{3}\) < 1.2
(C) 2m < 8.8
(D) 5m < 22
Answer:
(C) 2m < 8.8

Explanation:
We can notice that the solution of inequality at C represents the number line below, really:
\(\frac{2m}{2}\) < \(\frac{8.8}{2}\)
m < 4.4
C) m < 4.4

Hot Tip! When possible, use logic to eliminate at least two answer choices.

Question 9.
Brian is playing a video game. He earns the same number of points for each star he picks up. He earned 2,400 points for 6 stars, 4,000 points for 10 stars, and 5,200 points for 13 stars. Which is the independent variable in the situation?
(A) the number of stars picked up
(B) the number of points earned
(C) the number of hours played
(D) the number of stars available
Answer:
(A) the number of stars picked up

Explanation:
Brian is playing a video game. He earns the same number of points for each star he picks up. Therefore, here the number of stars picked is the independent quantity.
option A

Question 10.
Which ratio is not equivalent to the other three?
(A) \(\frac{2}{5}\)
(B) \(\frac{12}{25}\)
(C) \(\frac{6}{15}\)
(B) \(\frac{18}{45}\)
Answer:
(B) \(\frac{12}{25}\)

Explanation:
Solution to this example is given below

Question 11.
One inch is 2.54 centimeters. About how many centimeters is 4.5 inches?
(A) 1.8 centimeters
(B) 11.4 centimeters
(C) 13.7 centimeters
(D) 114 centimeters
Answer:
(B) 11.4 centimeters

Explanation:
Solution to this example is given below
1 inch = 2.54 centimeters.
4.5 inch = x centimeters

x = 11.43 centimeters
B This option is correct answer

Gridded Response

Questions 12.
The area of a rectangular mural is 84 square feet. The mural’s width is 7 feet. What is its length in feet?

Answer:
The area of a rectangular mural is a product of its width and its length, so, we get the following equation, according to this:
84 = 7x
Where x represents a length of this mural in feet. In order to solve it, we need to divide both by 7 and get:
\(\frac{84}{7}\) = \(\frac{7 x}{7}\)
12 = x
So, the length of this mural is 12 feet.
12 feet

Question 13.
What is the y-coordinate of point 6 on the coordinate grid below?

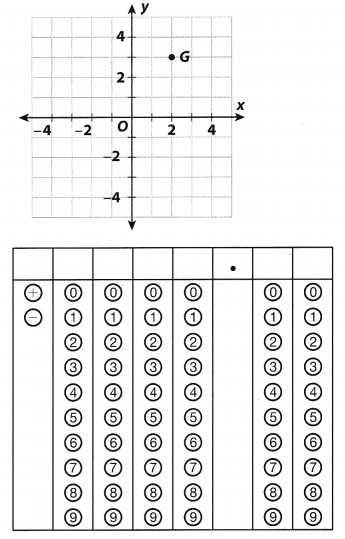
Answer:
We can see that point on x-axes which is corresponding to G is 2 and the corresponding point on y-axes is 3 point
So, conclusion is that corresponding y-coordinate is 3.
3

Hot Tip!
Gridded responses can be positive or negative numbers. Enter any negative signs in the first column. Check your work!

Question 14.
When traveling in Canada, Patricia converts the temperature given in degrees Celsius to a Fahrenheit temperature by using the expression 9x ÷ 5 + 32, where x is the Celsius temperature. Find the temperature in degrees Fahrenheit when it is 25°C.

Answer:
In order to find the temperature in degrees Fahrenheit, we will substitute 25 for x in the equation from this task and get:
9 • 25 ÷ 5 + 32 = 225 ÷ 5 + 32
45 + 32 = 77
So 25°C is actually 77 degrees in Fahrenheit
77°F

Vocabulary Preview

Use the puzzle to preview key vocabulary from this unit. Unscramble the circled letters within found words to answer the riddle at the bottom of the page.

• A number that is multiplied by a variable in an algebraic expression. (Lesson 11-l)
• A value of the variable that makes the equation true. (Lesson 12-1)
• The numbers in an ordered pair. (Lesson 14-1)
• The point where the axes intersect to form the coordinate plane. (Lesson 14-1)
• The part of an expression that is added or subtracted. (Lesson 11-1)
• The two number lines that intersect at right angles to form a coordinate plane. (Lesson 14-1)
• Tells how many times the base is used in the product. (Lesson 10-1)

Q: Why did the paper rip when the student tried to stretch out the horizontal axis of his graph?
A. Too much __ – __ __ __ __ __ !