Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Module 8 Answer Key Applying Ratios and Rates.
Texas Go Math Grade 6 Module 8 Answer Key Applying Ratios and Rates
Texas Go Math Grade 6 Module 8 Are You Ready? Answer Key
Graph each point on the coordinate grid above.
Question 1.
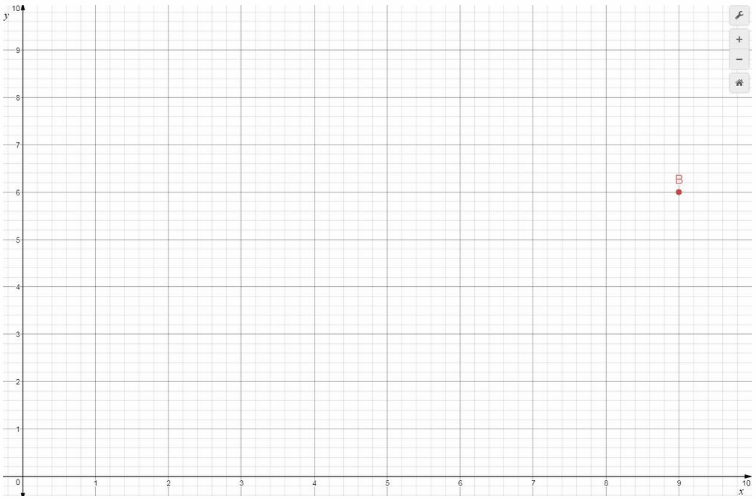
B(9, 6)
Answer:
The point B(9, 6) locate on an xy-coordinate graph, go nine units from the origin to the right to 6 on the horizontal axis and then, from that point. go 6 units up (using the y-axis scale).
Question 2.
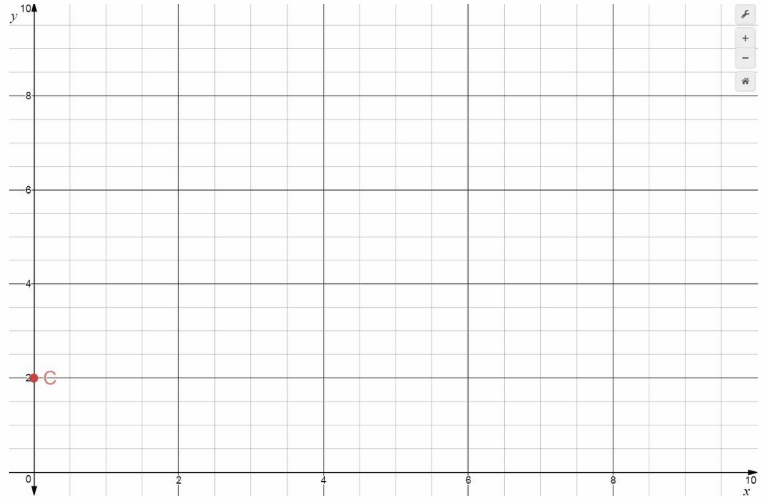
C(0, 2)
Answer:
The point C(0, 2) locate on an xy-coordinate graph, go zero units from the origin to 0 on the horizontal axis and then, from that point, go 2 units up (using the y-axis scale).
Question 3.
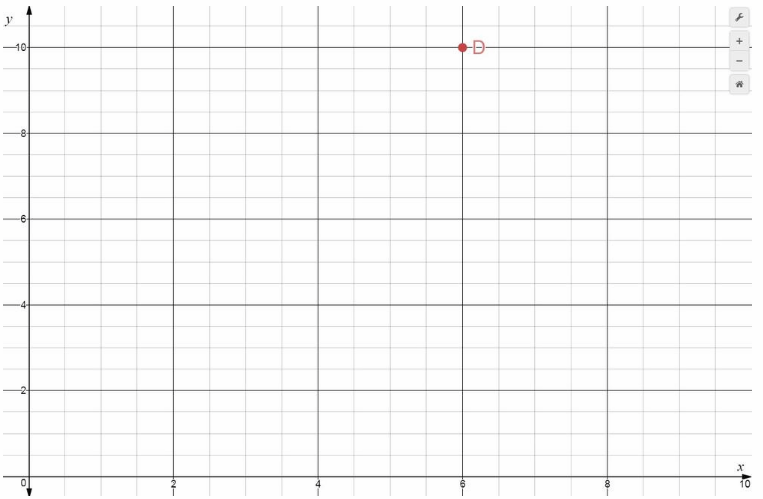
D(6, 10)
Answer:
The point D(6, 10) locate on an xy-coordinate graph, go six units from the origin to the right to 6 on the horizontal axis and then, from that point, go 10 units up (using the y-axis scale).
Question 4.
E(3, 4)
Answer:
The point E(3, 4) locate on an xy-coordinate graph, go three units from the origin to the right to 3 on the horizontal axis and then, from that point, go 4 units up (using the y-axis scale).
Write the equivalent fractions.
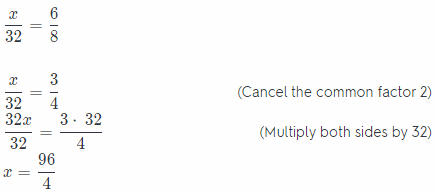
Question 5.
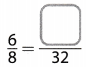
Answer:
Switch sides

x = 24
The equivalent fractions becomes
\(\frac{6}{8}=\frac{24}{32}\)
Question 6.
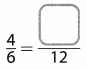
Answer:
Switch Sides

x = 7
The equivalent fractions becomes
\(\frac{1}{8}=\frac{7}{56}\)
Question 7.
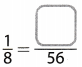
Answer:
Switch Sides

x = 7
The equivalent fractions becomes
\(\frac{1}{8}=\frac{7}{56}\)
Question 8.
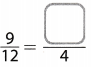
Answer:
Switch Sides

x = 3
The equivalent fractions becomes
\(\frac{9}{12}=\frac{3}{4}\)
Question 9.
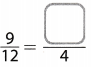
Answer:
First we use this rule
Apply fraction cross multiply: if \(\frac{a}{b}=\frac{c}{d}\) then a ∙ d = b ∙ c
5x = 9 ∙ 25
5x = 225 (Multiply the numbers)
\(\frac{5 x}{5}=\frac{225}{5}\) (Divide both sides by 5)
x = 25
The equivalent fraction becomes
\(\frac{5}{9}=\frac{25}{45}\)
Question 10.

Answer:
First we use this rule
Apply fraction cross multiply: if \(\frac{a}{b}=\frac{c}{d}\) then a ∙ d = b ∙ c
5x = 6 ∙ 20
5x = 120 (Multiply the numbers)
\(\frac{5 x}{5}=\frac{120}{5}\) (Divide both sides by 5)
x = 24
The equivalent fraction becomes
\(\frac{5}{6}=\frac{20}{24}\)
Question 11.
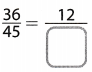
Answer:
First we use this rule
Apply fraction cross multiply: if \(\frac{a}{b}=\frac{c}{d}\) then a ∙ d = b ∙ c
36x = 45 ∙ 12
36x = 540 (Multiply the numbers)
\(\frac{36 x}{36}=\frac{540}{36}\) (Divide both sides by 5)
x = 15
The equivalent fraction becomes
\(\frac{36}{45}=\frac{12}{15}\)
Question 12.
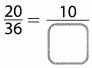
Answer:
First we use this rule
Apply fraction cross multiply: if \(\frac{a}{b}=\frac{c}{d}\) then a ∙ d = b ∙ c
20x = 36 ∙ 10
20x = 360 (Multiply the numbers)
\(\frac{20 x}{20}=\frac{360}{20}\) (Divide both sides by 20)
x = 18
The equivalent fraction becomes
\(\frac{20}{36}=\frac{10}{18}\)
List the first five multiples of each number.
Question 13.
3 ______________
Answer:
List the first five multiples of 3
3 × 1 = 3
3 × 2 = 6 (Multiply 3 by the numbers 1, 2,)
3 × 3 = 9 (3, 4, and 5)
3 × 4 = 12
3 × 5 = 15
3, 6, 9, 12, 15
Question 14.
7 ______________
Answer:
List the first five multiples of 7
7 × 1 = 7
7 × 2 = 14 (Multiply 7 by the numbers 1, 2,)
7 × 3 = 21 (3, 4 and 5)
7 × 4 = 28
7 × 5 = 35
7, 14, 21, 28, 35
Question 15.
8 ______________
Answer:
List the first five multiples of 8
8 × 1 = 8
8 × 2 = 16 (Multiply 8 by the numbers 1, 2,)
8 × 3 = 24 (3, 4, and 5)
8 × 4 = 32
8 × 5 = 40
8, 16, 24, 32, 40
Texas Go Math Grade 6 Module 8 Reading Start-Up Answer Key
Visualize Vocabulary
Use the ✓ words to complete the graphic. Comparing Unit Rates

Understand Vocabulary
Complete the sentences using the preview words.
Question 1.
A __________________ is a rate that compares two equivalent measurements.
Answer:
Conversion factor
Question 2.
The two sides that form the right angle of a right triangle are called __________________. The side opposite the right angle in a right triangle is called the __________________ .
Answer:
cathetus, hypotenuse