Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 10 Quiz Answer Key.
Texas Go Math Grade 6 Module 10 Quiz Answer Key
10.1 Exponents
Find the value of each power.
Question 1.
73
Answer:
Solution to this example is given below 73
Identify the base and the exponent.
The base is 7 and the exponent is 3.
Final Solution:
Evaluate: 73 = 7 × 7 × 7 = 343
Question 2.
92
Answer:
Solution to this example is given below 92
Identify the base and the exponent.
The base is 9 and the exponent is 2.
Final Solution:
Evaluate: 92 = 9 × 9 = 81
Question 3.
\(\left(\frac{7}{9}\right)^{2}\)
Answer:
Solution to this example is given below \(\left(\frac{7}{9}\right)^{2}\)
Identify the base and the exponent.
The base is \(\frac{7}{9}\) and the exponent is 2.
Final Solution:
Evaluate: \(\left(\frac{7}{9}\right)^{2}\) = \(\frac{7}{9} \times \frac{7}{9}\) = \(\frac{79}{81}\)
Question 4.
\(\left(\frac{1}{2}\right)^{6}\)
Answer:
Solution to this example is given below \(\left(\frac{1}{2}\right)^{6}\)
Identify the base and the exponent.
The base is \(\frac{1}{2}\) and the exponent is 6.
Final Solution:
Evaluate: \(\left(\frac{1}{2}\right)^{6}\) = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\) = \(\frac{1}{64}\)
Question 5.
\(\left(\frac{2}{3}\right)^{3}\)
Answer:
Solution to this example is given below \(\left(\frac{2}{3}\right)^{3}\)
Identify the base and the exponent.
The base is \(\frac{2}{3}\) and the exponent is 3.
Final Solution:
Evaluate: \(\left(\frac{2}{3}\right)^{3}\) = \(\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\) = \(\frac{8}{27}\)
Question 6.
(- 3)5
Answer:
Simplify the given expression by identifying the base and exponent
The base is – 3 and the exponent is 5.
= (- 3) × (- 3) × (- 3) × (- 3) × (- 3) multiply the base by itself five times
= – 243
The simplified expression is – 243.
Question 7.
(- 2)4
Answer:
Simplify the given expression by identifying the base and exponent.
The base is – 2 and the exponent is 4.
= (- 2) × (- 2) × (- 2) × (- 2) multiply the base by itself four times
= 16
The simplified expression is 16.
Question 8.
1.42
Answer:
Solution to this example is given below 1.42
Identify the base and the exponent.
The base is 1.4 and the exponent is 2.
Final Solution:
Evaluate: 1.42 = 1.4 × 1.4 = 1.96
10.2 Prime Factorization
Find the factors of each number.
Question 9.
96 _________________
Answer:
List the factors of 96
- 96 = 1 × 96
- 96 = 2 × 48
- 96 = 3 × 32
- 96 = 4 × 24
- 96 = 6 × 16
- 96 = 8 × 12
The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96.
Question 10.
120 ________________
Answer:
List the factors of 120
- 120 = 1 × 120
- 120 = 2 × 60
- 120 = 3 × 40
- 120 = 5 × 24
- 120 = 6 × 20
- 120 = 8 × 15
- 120 = 10 × 12
The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 60 and 120.
Find the prime factorization of each number.
Question 11.
58 ________________
Answer:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 58 are 2, and 29.
The prime factorization of 58 is 2 × 29
Question 12.
212 _______________
Answer:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 212 are 2, 2 and 53.
The prime factorization of 212 is 2 × 2 × 53 or 22 × 53
Question 13.
2,800 ______________
Answer:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 2800 are 2, 2, 2, 2, 5, 5 and 7.
The prime factorization of 2800 is 2 × 2 × 2 × 2 × 5 × 5 × 7 or 24 × 52 × 7
Question 14.
900 ______________
Answer:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 900 are 2, 2, 3, 3, 5 and 5.
The prime factorization of 2800 is 2 × 2 × 3 × 3 × 5 × 5 or 22 × 32 × 52
10.3 Order of Operations
Simplify each expression using the order of operations.
Question 15.
(21 – 3) ÷ 32
Answer:
Solution to this example is given below
(21 – 3) ÷ 32
(21 – 3) ÷ 32 = (21 – 3) ÷ 9 Evaluate 32
= 18 ÷ 9 Perform operations inside parentheses.
= 2 Divide.
= 2
Question 16.
72 × (6 ÷ 3)
Answer:
Solution to this example is given below
72 × (6 ÷ 3)
72 × (6 ÷ 3)> = 49 × (6 ÷ 3) Evaluate 72
= 49 × 2 Perform operations inside parentheses.
= 98 Multiply.
= 98
Question 17.
17 + 15 ÷ 3 – 24
Answer:
Solution to this example is given below
17 + 15 ÷ 3 – 24
17 + 15 ÷ 3 – 24 = 17 + 15 ÷ 3 – 16 Evaluate 24.
= 17 + 5 – 16 Divide.
= 22 – 16 Add.
= 6 Subtract.
= 6
Question 18.
(8 + 56) ÷ 4 – 32
Answer:
Solution to this example is given below
(8 + 56) ÷ 4 – 32
(8 + 56) ÷ 4 – 32 = (8 + 56) ÷ 4 – 9 Evaluate 32.
= 64 ÷ 4 – 9 Perform operations inside parentheses.
= 16 – 9 Divide.
= 7 Subtract.
= 7
Question 19.
The nature park has a pride of 7 adult lions and 4 cubs. The adults eat 6 pounds of meat each day and the cubs eat 3 pounds. Simplify 7 × 6 + 4 × 3 to find the amount of meat consumed each day by the lions.
Answer:
Solution to this example ¡s given below 7 × 6 + 4 × 3
7 × 6 + 4 × 3 = 7 × 6 + 12 Multiply.
= 42 + 12 Multiply.
= 54 Add.
= 1
Each day by the lions is equal to 54 pounds.
Essential Question
Question 20.
How do you use numerical expressions to solve real-world problems?
Answer:
Most real world problems can be converted to algebraic expressions and equations to solve them. For example if a person earns a fixed monthly salary of $x and has expenses a, b and c, then the expenses can be added to evaluate the total expenses of the month and this sum can be subtracted front the amount of monthly salary to evaluate monthly savings and so on.
Texas Go Math Grade 6 Module 10 Mixed Review Texas Test Prep Answer Key
Selected Response
Question 1.
Which expression has a value that is less than the base of that expression?
(A) 23
(B) \(\left(\frac{5}{6}\right)^{2}\)
(C) 32
(D) 44
Answer:
(B) \(\left(\frac{5}{6}\right)^{2}\)
Explaination:
Identify the expression which has a value of less than the basa
(A) The base is 2 and the exponent is 3.
= 2 × 2 × 2 multiply the base three times
= 8
8 is not less than 2
(B) The base is 2 and the exponent is 3.
= \(\frac{5}{6} \times \frac{5}{6}\) multiply the base twice
= \(\frac{25}{36}\)
\(\frac{25}{36}\) is less than \(\frac{5}{6}\)
(C) The base is 3 and the exponent is 2.
= 3 × 3 multiply the base twice
= 9
9 is not less than 3
(D) The base is 2 and the exponent is 3.
= 4 × 4 × 4 × 4 multiply the base tour times
= 256
256 is not less than 4
The expression with a value less than the base is B. \(\left(\frac{5}{6}\right)^{2}\) because the base is a fraction.
Question 2.
After the game the coach bought 9 chicken meals for $5 each and 15 burger meals for $6 each. What percent of the total amount the coach spent was used for the chicken meals?
(A) 33\(\frac{1}{3}\)%
(B) 45%
(C) 66\(\frac{2}{3}\)%
(D) 90%
Answer:
(A) 33\(\frac{1}{3}\)%
Explaination:
Solution to this example is given below
9 × 5 + 15 × 6
9 × 5 + 15 × 6 = 9 × 5 + 90 Multiply.
= 45 + 90 Multiply.
= 135 Add.
We now calculate the percentage
Percent = \(\frac{45}{135}\) × 100%
= \(\frac{4500}{135}\)
= 33\(\frac{1}{3}\)%
Question 3.
Which operation should you perform first when you simplify 75 – (8 + 45 ÷ 3) × 7?
(A) addition
(B) division
(C) multiplication
(D) subtraction
Answer:
(B) division
Explaination:
Solution to this example is given below
175 – (8 + 45 ÷ 3) × 7
175 – (8 + 45 ÷ 3) × 7 = 175 – (8 + 15) × 7 [Divide.]
= 175 – 23 × 7 [Perform operations inside parentheses.]
= 175 – 161 [Multiply.]
= 14 [Subtract.]
B is the correct option
Division is first operation
Question 4.
At Tanika’s school, three people are chosen in the first round. Each of those people chooses 3 people in the second round, and so on. How many people are chosen in the sixth round?
(A) 18
(B) 216
(C) 243
(D) 729
Answer:
(D) 729
Explaination:
First round = 31 = 3
Second round = 32 = 9
Third round = 33 = 27
Fourth round = 34 = 81
Fifth round = 35 = 243
Sixth round = 36 = 729
There are 729 people chosen in the sixth round.
Question 5.
Which expression shows the prime factorization of 100?
(A) 22 × 52
(B) 10 × 10
(C) 1010
(D) 2 × 5 × 10
Answer:
(A) 22 × 52
Explaination:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 100 are 2, 2, 5 and 5
The prime factorization of 100 is 2 × 2 × 5 × 5 or 22 × 52
Question 6.
Which number has only two factors?
(A) 21
(B) 23
(C) 25
(D) 27
Answer:
(B) 23
Explaination:
Let’s check which number has two factors
(A) List the factors of 21
21 = 1 × 21
21 = 3 × 7
Option A is not correct answer
(B) List the factor of 23
23 = 1 × 23
Option B is correct answer
(C) List the factors of 25
25 = 1 × 25
25 = 5 × 5
Option C is not correct answer
(D) List the factors of 27
27 = 1 × 27
27 = 3 × 9
Option D is not correct answer
Question 7.
Which expression is equivalent to 3.6 × 3.6 × 3.6 × 3.6?
(A) 3.6 × 4
(B) 363
(C) 34 × 64
(D) 3.64
Answer:
(D) 3.64
Explaination:
Solution to this example is given below
3.6 × 3.6 × 3.6 × 3.6
Find the base, or the numbers being multiplied. The base is 3.6
Find the exponent by counting the number of the 3.6s being multiplied.
The exponent is 4
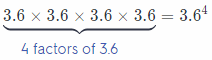
Question 8.
Which expression gives the prime factorization of 80?
(A) 24 × 10
(B) 2 × 5 × 8
(C) 23 × 5
(D) 24 × 5
Answer:
(D) 24 × 5
Explaination:
The prime factorization of a number is the number written as the product of its prime factors. For example, the prime factors of 80 are 2, 2, 2, 2 and 5.
The prime factorization of 80 is 2 × 2 × 2 × 2 × 5 or 24 × 5
Gridded Response
Question 9.
Alison raised 10 to the 5th power. Then she divided this value by 100. What was the quotient?
Answer:
Evaluate the expression.
= 105 ÷ 100 [evaluate the exponent]
= 100,000 ÷ 100 [divide the numbers]
= 1,000
The answer on the grid must be 1,000.