Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 3.4 Answer Key Dividing Mixed Numbers.
Texas Go Math Grade 6 Lesson 3.4 Answer Key Dividing Mixed Numbers
Reflect
Question 1.
Communicate Mathematical Ideas Which mathematical operation could you use to find the number of sushi rolls that Antoine can make? Explain.
Answer:
We can use dividing to find the number of sushi rolls that Antonie can make Actually, to find that number, we need to divide 2\(\frac{1}{2}\) by \(\frac{1}{4}\).
Question 2.
Multiple Representations Write the division shown by the model.
Answer:
The division shown by the previous model is the following:
2\(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
Question 3.
What If? Suppose Antoine instead uses \(\frac{1}{8}\) cup of rice for each sushi roll. How would his model change? How many rolls can he make? Explain.
Answer:
Instead dividing 2\(\frac{1}{2}\) by \(\frac{1}{8}\), he will divide 2\(\frac{1}{2}\) by \(\frac{1}{8}\) and in that case he will make more sushi rolls.
Question 4.
Analyze Relationships Explain how you can check the answer.
Answer:
We can check the answer dividing the result by the first of the fractions we were dividing or multiplying the result by the second of the fractions we were dividing.
Question 5.
What If? Harold serves himself 1\(\frac{1}{2}\)-ounce servings of cereal each morning. How many servings does he get from a box of his favorite cereal? Show your work.
Answer:
We need to divide 1 by 1\(\frac{1}{2}\) in order to get how many servings Harold gets from a box. But first we need to rewrite 1\(\frac{1}{2}\) as a fraction and find its reciprocal.
So, we have the following:
1\(\frac{1}{2}\) = \(\frac{3}{2}\)
Reciprocal of \(\frac{3}{2}\) is \(\frac{2}{3}\)
Now, we have to multiply 1 by \(\frac{2}{3}\) and get:
1 × \(\frac{2}{3}=\frac{1 \times 2}{1 \times 3}=\frac{2}{3}\)
So, Harold gets \(\frac{2}{3}\) servings of cereal from a box.
Your Turn
Question 6.
Sheila has 10\(\frac{1}{2}\) pounds of potato salad. She wants to divide the potato salad into containers, each of which holds 1\(\frac{1}{4}\) pounds. How many containers does she need? Explain.
Answer:
In order to find how many containers Sheila wilt need, we need to divide 10\(\frac{1}{2}\) by 1\(\frac{1}{4}\). But first we need to rewrite those mixed numbers as a fraction, than find reciprocal of the second one and then multiply them.
So, we get:
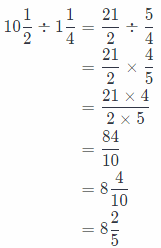
She will need 8\(\frac{2}{5}\) containers.
Reflect
Question 7.
Check for Reasonableness How can you determine if your answer is reasonable?
Answer:
If we have to divide two fractions, we can check our result on two ways:
First is to multiply result by the second fraction and if product is the first fraction, then our original solution is correct.
The second way is to divide the first fraction by result and if we get as a result of this dividing the second fraction, then our original solution is correct.
Multiply result by the second fraction; Divide the fraction by the result.
Your Turn
Question 8
The area of a rectangular patio is 12\(\frac{3}{8}\) square meters.
The width of the patio is 2\(\frac{3}{4}\) meters. What is the length? ___________
Answer:
First we will write given situation as a division problem, it is the following:
12\(\frac{3}{8}\) ÷ 2\(\frac{3}{4}\)
Now, we will rewrite the mixed numbers as fractions greater than 1.
12\(\frac{3}{8}\) ÷ 2\(\frac{3}{4}\) = \(\frac{99}{8}\) ÷ \(\frac{11}{4}\)
In the next step we will rewrite the problem as multiplication using the reciprocal of the second fraction:
\(\frac{99}{8} \div \frac{11}{4}=\frac{99}{8} \times \frac{4}{11}\)
Now, we will multiply previous fractions:
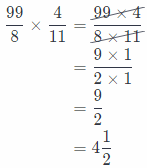
So, the length of a rectangular patio 4\(\frac{1}{2}\) meters.
Question 9.
The area of a rectangular rug is 14\(\frac{1}{2}\) square yards.
The length of the rug is 4\(\frac{1}{3}\) yards. What is the width? ___________
Answer:
First we wilt write given situation as a division problem, it is the following:
14\(\frac{1}{12}\) ÷ 4\(\frac{1}{3}\)
Now, we will rewrite the mixed numbers as fractions greater than 1.
14\(\frac{1}{12}\) ÷ 4\(\frac{1}{3}\) = \(\frac{169}{12} \div \frac{13}{3}\)
In the next step we will rewrite the problem as multiplication using the reciprocal of the second fraction:
\(\frac{169}{12} \div \frac{13}{3}=\frac{169}{12} \times \frac{3}{13}\)
Now, we will multiply previous fractions:
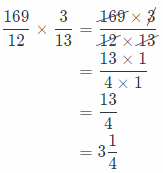
So, the width of a rectangular rug is 3\(\frac{1}{4}\) yards.
Texas Go Math Grade 6 Lesson 3.4 Guided Practice Answer Key
Divide. Write each answer in simplest form.
Question 1.
4\(\frac{1}{4}\) ÷ \(\frac{3}{4}\)
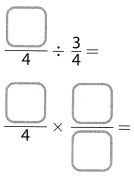
Answer:
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
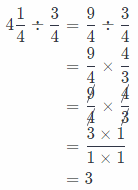
Conclusion is that the solution is 3.
Question 2.
1\(\frac{1}{2}\) ÷ 2\(\frac{1}{4}\)
Answer:
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
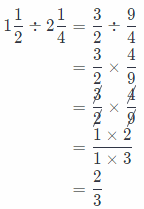
Conclusion is that the solution is \(\frac{2}{3}\).
Question 3.
4 ÷ 1\(\frac{1}{8}\) ____________
Answer:
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
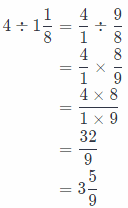
Conclusion is that the solution is \(\frac{32}{9}\), or 3\(\frac{5}{9}\).
Question 4.
3\(\frac{1}{5}\) ÷ 1\(\frac{1}{7}\) ____________
Answer:
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
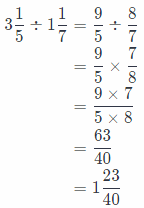
Conclusion is that the solution is \(\frac{63}{40}\), or 1\(\frac{23}{40}\).
Question 5.
8\(\frac{1}{3}\) ÷ 2\(\frac{1}{2}\) ____________
Answer:
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
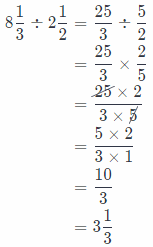
Conclusion is that the solution is \(\frac{10}{3}\), or 3\(\frac{1}{3}\).
Question 6.
15\(\frac{1}{3}\) ÷ 3\(\frac{5}{6}\) ____________
Answer:
Solution to this example is given below
First we will rewrite the mixed numbers as fractions greater than 1, then again rewrite the problem as multiplication
using the reciprocal ot the second fractions.
We will simplify using the GCF in order to get the solution in simplest form and multiply numerators and denominators. At the end, we will rewrite the solution as a mixed number if it is greater than 1.
So, we have the following:
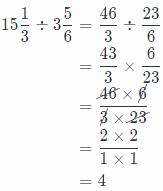
Conclusion is that the solution is 4.
Write each situation as a division problem. Then solve.
Question 7.
A sandbox has an area of 26 square feet, and the length is 5\(\frac{1}{2}\) feet. What is the width of the sandbox?
Answer:
First we will write given situation as a division problem, it is the following:
26 ÷ 5\(\frac{1}{2}\)
Now, we will rewrite the mixed numbers as fractions greater than 1.
26 ÷ 5\(\frac{1}{2}\) = \(\frac{26}{1}\) ÷ \(\frac{11}{2}\)
In the next step we will rewrite the problem as multiplication using the reciprocal of the second fraction:
\(\frac{26}{1} \div \frac{11}{2}=\frac{26}{1} \times \frac{2}{11}\)
Now, we will multiply previous fractions:
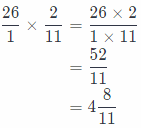
So, the width of the sandbox is 4\(\frac{8}{11}\) feet
Question 8.
Mr. Webster is buying carpet for an exercise room in his basement. The room will have an area of 230 square feet. The width of the room is 12\(\frac{1}{2}\) feet. What is the length?
Answer:
First we will write given situation as a division problem, it is the following:
230 ÷ 12\(\frac{1}{2}\)
Now, we will rewrite the mixed numbers as fractions greater than 1.
230 ÷ 12\(\frac{1}{2}\) = \(\frac{230}{1}\) ÷ \(\frac{25}{2}\)
In the next step we will rewrite the problem as multiplication using the reciprocal of the second fraction:
\(\frac{230}{1} \div \frac{25}{2}=\frac{230}{1} \times \frac{2}{25}\)
Now, we will multiply previous fractions:
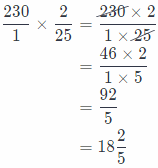
So, the length of the room is 18\(\frac{2}{5}\) feet.
Essential Question Check-In
Question 9.
How does dividing mixed numbers compare with dividing fractions?
Answer:
We have to rewrite mixed numbers as a fractions greater than 1 and then the steps of dividing are the same as dividing two fractions because we actually get two fractions.
It is equivalent with dividing fractions, but first rewrite mixed numbers as mixed numbers.
Question 10.
Jeremy has 4\(\frac{1}{2}\) CUPS of iced tea. He wants to divide the tea into \(\frac{3}{4}\)-cup servings. Use the model to find the number of servings he can make.
![]()
Answer:
We will use the following model in order to find the number of servings Jeremy can make:
4\(\frac{1}{2}\) ÷ \(\frac{3}{4}\)
We will rewrite mixed number as a fraction and rewrite the model as multiplication using the reciprocal of the
second fractions.
And then multiply fractions:
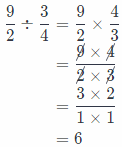
So, Jeremy can make 6 servings
Question 11.
A ribbon is 3\(\frac{2}{3}\) yards long. Mae needs to cut the ribbon into pieces that are \(\frac{2}{3}\) yard long. Use the model to find the number of pieces she can cut.

Answer:
We will use the following model in order to find the number of servings Jeremy can make:
3\(\frac{2}{3}\) ÷ \(\frac{2}{3}\)
We will rewrite mixed number as a fraction and rewrite the model as multiplication using the reciprocal of the
second fractions.
And then multiply fractions:
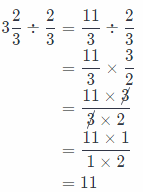
So, Mae can cut 11 pieces of a ribbon.
Question 12.
Dao has 2\(\frac{3}{8}\)pounds of hamburger meat. He is making \(\frac{1}{4}\)-pound hamburgers. Does Dao have enough meat to make 10 hamburgers? Explain.
Answer:
In order to find the number of hamburgers Dao can make of 2\(\frac{3}{8}\) pounds of hamburger meat, we have to divide 2\(\frac{3}{8}\) by \(\frac{1}{4}\).
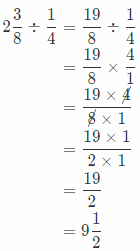
Dao can make 9\(\frac{1}{4}\) hamburgers. Conclusion is that Dao has not enough meat for making 10 hamburgers.
Question 13.
Multistep Zoey made 5\(\frac{1}{2}\) cups of trail mix fora camping trip. She wants to divide the trail mix into \(\frac{3}{4}\)-cup servings.
a. Ten people are going on the camping trip. Can Zoey make enough \(\frac{3}{4}\)-cup servings so that each person on the trip has one serving?
Answer:
We will find number of serving Zoey can made dividing 5\(\frac{1}{2}\) by \(\frac{3}{4}\).
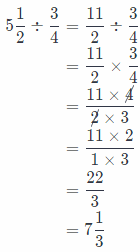
So, we can notice that there are 7\(\frac{1}{3}\) sevings.
Conclusion is that there is not enough servings for 10 persons.
b. What size would the servings need to be for everyone to have a serving? Explain.
Answer:
If we want to share 2\(\frac{3}{8}\) cups of trail mix to 10 persons, we need to divide 2\(\frac{3}{8}\) by 10 in order to get size of each serving:
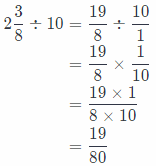
So, size of each serving would be \(\frac{19}{80}\)-cup.
c. If Zoey decides to use the \(\frac{3}{4}\)-cup servings, how much more trail mix will she need? Explain.
Answer:
To calculate how much more trail mix Zoey will need for 10 persons, we need to subtract 7\(\frac{1}{3}\), result we get at (a), from 10:
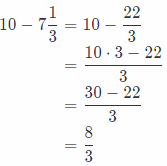
So, Zoey will need \(\frac{8}{3}\)-cup of trail mix moreS
Question 14.
The area of a rectangular picture frame is 3o\(\frac{1}{3}\) square inches. The length of the frame is 6\(\frac{1}{2}\) inches. Find the width of the frame.
Answer:
First we will write given situation as a division problem, it is the following:
30\(\frac{1}{3}\) ÷ 6\(\frac{1}{2}\)
Now, we will rewrite the mixed numbers as fractions greater than 1.
20\(\frac{1}{3}\) ÷ 6\(\frac{1}{2}\) = \(\frac{91}{3}\) ÷ \(\frac{13}{2}\)
In the next step we will rewrite the problem as multiplication using the reciprocal of the second fraction:
\(\frac{91}{3} \div \frac{13}{2}=\frac{91}{3} \times \frac{2}{13}\)
Now, we will multiply previous fractions:
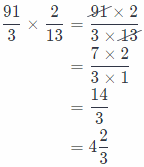
So, the width of the frame is 4\(\frac{2}{3}\) inches.
Question 15.
The area of a rectangular mirror is 11\(\frac{11}{16}\) square feet. The width of the mirror is 2\(\frac{3}{4}\)feet. If there is a 5 foot tall space on the wall to hang the mirror, will it fit? Explain.
Answer:
We need to find the length of the mirror dividing 11\(\frac{11}{16}\) by 2\(\frac{3}{4}\). So, we have the following:
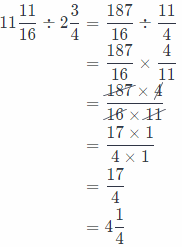
We got that the Length of mirror is 4\(\frac{1}{4}\) feet and there is a 5 feet total space on the wall for hanging the mirror, so, 4\(\frac{1}{4}\) < 5, there is enough space on the wall for hanging mirror, it will fit.
Question 16.
Ramon has a rope that is 25\(\frac{1}{2}\) feet long. He wants to cut it into 6 pieces that are equal in length. How long will each piece be?
Answer:
In order to find length of each peace, we have to divide 25\(\frac{1}{2}\) by 6, so we have following:
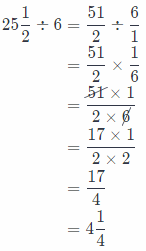
So, each piece will be long 4\(\frac{1}{4}\) feet.
Question 17.
Eleanor and Max used two rectangular wooden boards to make a set for the school play. One board was 6 feet long, and the other was 5\(\frac{1}{2}\) feet long. The two boards had equal widths. The total area of the set was 60\(\frac{3}{8}\) square feet. What was the width?
Answer:
We can conclude that total length of the set is:
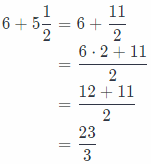
In order to total width of the set, we have to divide 60\(\frac{3}{8}\) by \(\frac{23}{3}\) and get:
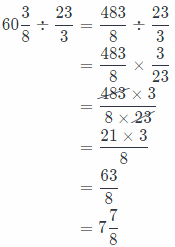
So, the total width of the set 7\(\frac{7}{8}\) feet.
H.O.T. Focus On Higher Order Thinking
Question 18.
Draw Conclusions Micah divided 11\(\frac{2}{3}\) by 2\(\frac{5}{6}\) and got 4\(\frac{2}{17}\) for an answer.
Does his answer seem reasonable? Explain your thinking. Then check Micah’s answer.
Answer:
Yes, Micah’s answer seems reasonabLe because 4\(\frac{2}{17}\) is smaller than 11\(\frac{2}{3}\), now we will also check it:
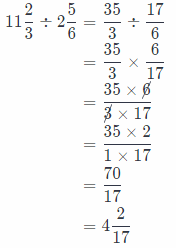
We can see that Micah’s answer is correct.
Question 19.
Explain the Error To divide 14\(\frac{2}{3}\) ÷ 2\(\frac{3}{4}\), Erik multiplied 14\(\frac{2}{3}\) × \(\frac{4}{3}\). Explain Erik’s error.
Answer:
Erik’s error was that he did not first rewrite mixed numbers as a fractions and then multiply them using the reciprocal of the second fraction.
So, the right way is:
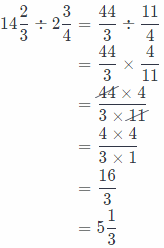
He did not first rewrite mixed numbers as a fractions.
Question 20.
Analyze Relationships Explain how you can find the missing number in 3\(\frac{4}{5}\) ÷ = 2\(\frac{5}{7}\). Then find the missing number.
Answer:
We will find the missing number dividing 3\(\frac{4}{5}\) by 2\(\frac{5}{7}\)
First, we will rewrite those mixed numbers as a fractions greater than 1.
Then rewrite the problem. First we need to rewrite the mixed numbers as a fractions grater than 1.
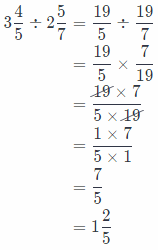
So, the missing number is \(\frac{7}{5}\), or 1\(\frac{2}{5}\).