Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 3.1 Answer Key Multiplying Fractions.
Texas Go Math Grade 6 Lesson 3.1 Answer Key Multiplying Fractions
Texas Go Math Grade 6 Lesson 3.1 Explore Activity Answer Key
Modeling Fraction Multiplication
Sam and Pete had a party. After the party, they discovered that \(\frac{3}{4}\) of a casserole was left over. Sam and Pete ate \(\frac{1}{2}\) of the leftover casserole. What fraction of the original casserole did Sam and Pete eat?
Shade the model to show 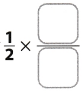 .
.
(A) Shade the rectangle to represent the \(\frac{3}{4}\) of the casserole that was left over after the party.
(B) Double shade \(\frac{1}{2}\) of \(\frac{3}{4}\). Divide the remaining fourth into two parts so that all of the parts are equal.
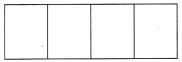
(C) Sam and Pete ate ____ of the original casserole.
(D) Did the amount of casserole increase or decrease when multiplied by \(\frac{1}{2}\)? How does the model show this? Explain.
(E) Write the multiplication shown by the model. 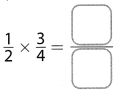
Reflect
Question 1.
Communicate Mathematical Ideas Will the product of \(\frac{1}{2}\) and \(\frac{2}{3}\) be greater or less than \(\frac{2}{3}\)? Explain.
Answer:
We can calculate the product of \(\frac{1}{2}\) and \(\frac{2}{3}\) and then compare the result with \(\frac{2}{3}\).
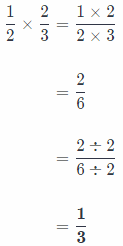
Now, we can compare \(\frac{1}{2}\) and \(\frac{2}{3}\)
Easiest way is to compare their numerators.
Number 1 is less than 2.
Therefore. we can write: 1 < 2
That implies that \(\frac{1}{3}\) is less than \(\frac{2}{3}\).
Question 2.
Communicate Mathematical Ideas Is the product less than or greater than the factors? Explain.
Answer:
This question depends on whether we multiply numbers whose value is greater than 1 or less than 1.
If both factors are greater than 1, then we get number which is greater than factors.
If any of factors is less than 1, then we get number which is less than at least one factor.
Question 3.
Analyze Relationships How can you determine when to simplify using the GCF before multiplying?
Answer:
We simplify our fractions using GCF when we see some common factor in numerator and denominator.
Your Turn
Multiply. Write each product in simplest form.
Question 4.
\(\frac{1}{6} \times \frac{3}{5}\) ____________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor
And finally, we write our answer in simplest form!
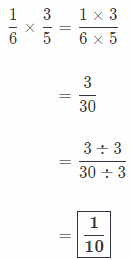
Question 5.
\(\frac{3}{4} \times \frac{7}{9}\) ____________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor
And finally, we write our answer in simplest form!
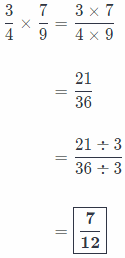
Question 6.
\(\frac{3}{7} \times \frac{2}{3}\) ____________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor
And finally, we write our answer in simplest form!
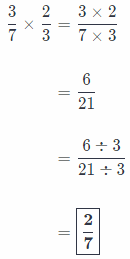
Question 7.
\(\frac{4}{5} \times \frac{2}{7}\) ____________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor
And finally, we write our answer in simplest form!
\(\frac{4}{5} \times \frac{2}{7}=\frac{4 \times 2}{5 \times 7}\)
= \(\frac{8}{35}\)
Reflect
Question 8.
Analyze Relationships Is the product of a fraction and a whole number greater than or less than the whole number? Explain.
Answer:
Product of a fraction and a whole number is greater than the whole number
if fraction numerator is greater than its denominator.
If fraction numerator is less than its denominator then the product is less than the whole number
There is also special case when fraction numerator and denominator are same, then the product is same as whole number.
Your Turn
Multiply. Write each product in simplest form.
Question 9.
\(\frac{5}{8}\) × 24 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
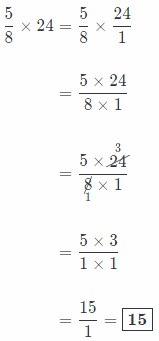
Question 10.
\(\frac{3}{5}\) × 20 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
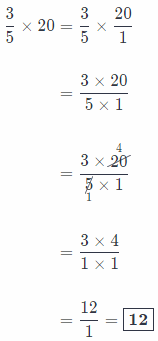
Question 11.
\(\frac{1}{3}\) × 8 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
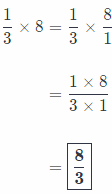
Question 12.
\(\frac{1}{4}\) × 14 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
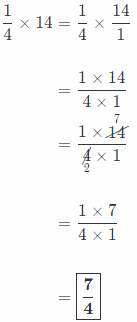
Question 13.
\(\frac{7}{10}\) × 7 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
\(\frac{7}{10}\) × 7 = \(\frac{7}{10} \times \frac{7}{1}\)
= \(\frac{7 \times 7}{10 \times 1}\)
= \(\frac{49}{10}\) = 4.9
Question 14.
\(\frac{7}{10}\) × 10 _______________
Answer:
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
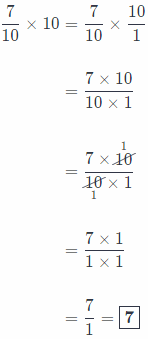
Texas Go Math Grade 6 Lesson 3.1 Guided Practice Answer Key
Question 1.
Lisa, Taryn, and Catherine go to a store to buy party supplies. The store has a sale on the supplies they want for the original price. The girls agree to each pay \(\frac{1}{3}\) of the cost. (Explore Activity)

a. Draw a model to show what fraction of the original price they will each pay.
Answer:
Discount:
Lisa
Taryn
Catherine
b. What fraction of the original price did each girl pay?
Answer:
As original, price was discounted to \(\frac{3}{4}\), and the girls agree to each pay \(\frac{1}{3}\) of the cost
So, each of them pays a third of a discounted price. We can write it as:
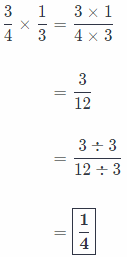
Now we know that each girl will pay \(\frac{1}{4}\) of the cost.
c. Write the multiplication shown by the model.
Answer:
As original, price was discounted to \(\frac{3}{4}\), and the girls agree to each pay \(\frac{1}{3}\) of the cost
So, each of them pays a third of a discounted price. We can write it as:
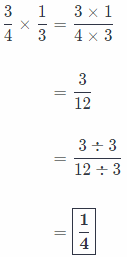
Now we know that each girl will pay \(\frac{1}{4}\) of the cost.
Done in task.
d. Did the fraction representing the sale price increase or decrease when multiplied by \(\frac{1}{3}\)? Explain.
Answer:
As we multiplied by a fraction whose numerator is less than denominator, we got a number which is less than the original one!
Multiply. Write each product in simplest form.
Question 2.
\(\frac{1}{2} \times \frac{5}{8}\) _______________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor.
And finally, we write our answer in simplest form!
\(\frac{1}{2} \times \frac{5}{8}=\frac{1 \times 5}{2 \times 8}\)
= \(\frac{5}{16}\)
Question 3.
\(\frac{3}{5} \times \frac{5}{9}\) _______________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor.
And finally, we write our answer in simplest form!
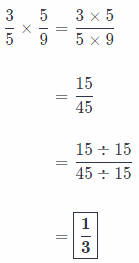
Question 4.
\(\frac{3}{8} \times \frac{2}{5}\) _______________
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simplify expression by dividing by the Greatest Common Factor.
And finally, we write our answer in simplest form!
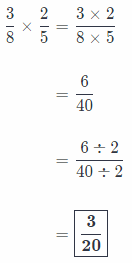
Find each amount.
Question 5.
\(\frac{1}{4}\) of 12 bottles of water = ______ bottles
Answer:
Here, if we want to get some ‘piece of stuff, we have to multiply the original value with given fractions!
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
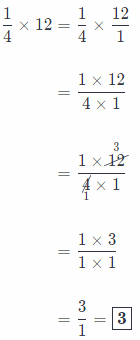
Therefore, \(\frac{1}{4}\) of 12 bottles of water equals 3 bottles of water!
Question 6.
\(\frac{2}{3}\) of 24 bananas = ______ bananas
Answer:
If we want to get some ‘piece of stuff, we have to multiply the original value with given fractions!
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
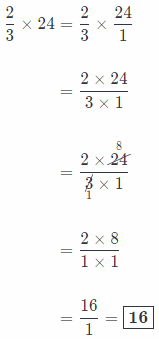
Therefore, \(\frac{2}{3}\) of 24 bananas equals 16 bananas
Question 7.
\(\frac{3}{5}\) of $40 restaurant bill = $ ______
Answer:
If we want to get some ‘piece of stuff, we have to multiply the original value with given fractions!
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
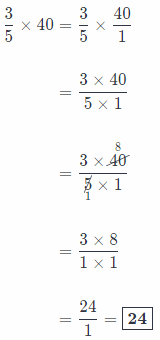
Therefore, \(\frac{3}{5}\) of $40 bill equals $24!
Question 8.
\(\frac{5}{6}\) of 18 pencils = ______ pencils
Answer:
If we want to get some ‘piece of stuff, we have to multiply the original value with given fractions!
Here, before we start the process of multiplication, we must write whole number as an equivalent fraction.
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we simplify before multiplying using the Greatest Common Factor.
Thirdly, we multiply numerators and denominators.
And finally, we write our solution in simplest form, as whole number if possible!
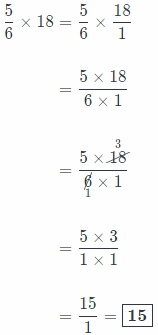
Thferefore, \(\frac{5}{8}\) of 18 pencils equals 15 pencils!
Essential Question Check-In
Question 9.
How can you multiply two fractions?
Answer:
Process of fractions multiplication:
Firstly, we write the problem as a single fraction.
Secondly, we multiply numerators and denominators!
Thirdly, we simpLify expression by dividing by the Greatest Common Factor.
And finally, we write our answer in simplest form!
Solve. Write each answer in simplest form.
Question 10.
Erin buys a bag of peanuts that weighs \(\frac{3}{4}\) of a pound. Later that week, the bag is \(\frac{2}{3}\) full. How much does the bag of peanuts weigh now? Show your work.
Answer:
In this task, we have a full, bag of peanuts that weights \(\frac{3}{4}\) pounds.
Later that week, there is only \(\frac{2}{3}\) of peanuts bag left
Now, we can conclude that the only way to find our solution is to multiply full bag weight with “new” weight
Note that we won’t write process of multiplication here since it can be found in previous tasks explained briefly!
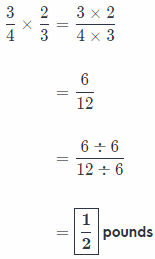
Question 11.
Multistep Marianne buys 16 bags of potting soil that comes in \(\frac{5}{8}\)-pound bags.
a. How many pounds of potting does Marianne buy?
Answer:
If we want to find weight of 16 bags of potting soil, we have to multiply the quantity with weight of single bag, which is \(\frac{5}{8}\) pounds.
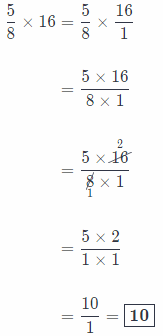
Now we know that Marianne buys 10 pounds of potting!
b. If Marianne’s father calls and says he needs 13 pounds of potting soil, will 4 more bags be enough to cover the extra soil needed?
Answer:
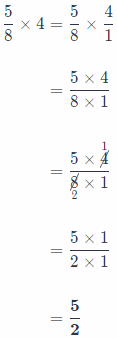
Now, final thing to do is to compare the weight of 18 bags with needed 13 pounds of potting
10 + \(\frac{5}{2}\) = 10 + 2.5 = 12.5
Now, we know that: 12.5 < 13 pounds.
So, conclusion is that 4 extra soil bags won’t be enough to cover her father’s needs!
Division:
![]()
Question 12.
Analyze Relationships Name three different pairs of fractions that have the same product when multiplied. Explain how you found them.
Answer:
First
\(\frac{5}{4} \times \frac{5}{2}\) = \(\frac{25}{8}\)
Secondly
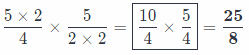
Third
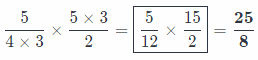
As we can see, all the pairs were obtained by multiplying numerator/denominator of one fractions and denominator/numerator of second fraction by same number!
Question 13.
Marcial found a recipe for fruit salad that he wanted to try to make for his birthday party. He decided to triple the recipe.
a. What is the new amount for the oranges, apples, blueberries, and peaches?
Answer:
As she tripled the recipe, now we have to triple the original amount of each fruit.
Blueberries:
\(\frac{1}{4}\) × 3 = \(\frac{1}{4}\) × \(\frac{3}{1}\)
= \(\frac{1 \times 3}{4 \times 1}\)
= \(\frac{3}{4}\)
New amount of Blueberries is \(\frac{3}{4}\) cup.
Oranges:
\(\frac{1}{2}\) × 3= \(\frac{1}{2}\) × \(\frac{3}{1}\)
= \(\frac{1 \times 2}{3 \times 1}\)
= \(\frac{3}{2}\)
New amount of Orange is \(\frac{3}{2}\) pieces.
Apples:
\(\frac{3}{5}\) × 3 = \(\frac{3}{5}\) × \(\frac{3}{1}\)
= \(\frac{3 \times 5}{3 \times 1}\)
= \(\frac{9}{5}\)
New amount of Apples is \(\frac{9}{5}\) pieces.
Peaches.
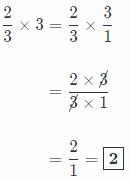
New amount of peaches is 2 pieces.
b. Communicate Mathematical Ideas The amount of rhubarb in the original recipe is 3 cups. Using what you know of whole numbers and what you know of fractions, explain how you could triple that mixed number.
Answer:
Let’s write the process of tripling the amount of rhubarb.
(1) Transforming mixed number into fraction
3\(\frac{1}{2}\) = 1 + 1 + 1 + \(\frac{1}{2}\)
= \(\frac{2}{2}+\frac{2}{2}+\frac{2}{2}+\frac{1}{2}\)
= \(\frac{7}{2}\)
(2) Multiplying fraction by 3:
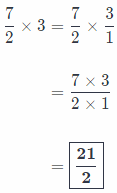
As Calculations says, new amount of rhubarb is \(\frac{21}{2}\) cups.
Question 14.
Music Two-fifths of the instruments in the marching band are brass. One-eighth of the brass instruments are tubas.
a. What fraction of the band is tubas?
Answer:
If there are \(\frac{2}{5}\) of instruments brass, and \(\frac{1}{8}\) of the brass instruments are tubas,
Amount of tubas is equal to product of those 2 fractions!
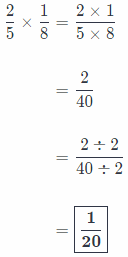
Now we know that \(\frac{1}{20}\) of all instruments in band are tubas.
b. If there are 240 band instruments total, how many are tubas?
Answer:
If there are 240 instruments in band, then there are:
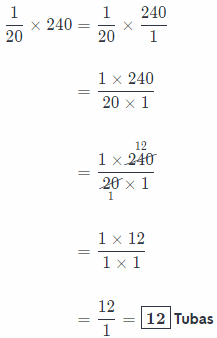
Division:
Question 15.
Compare simplifying before multiplying fractions with simplifying after multiplying the fractions.
Answer:
Simplifying before multiplying fractions will give us the same result as simplifying after multiplying the fractions!
However, simplifying before multiplying fractions has some benefits.
For example, when we have some larger number in numerator and denominator with common factor greater than I, we can simply reduce them to lower the amount of work after multiplication.
Question 16.
Sports Kevin is a quarterback on the football team. He completed 36 passes during the season. His second-string replacement, Mark, completed \(\frac{2}{9}\) as many passes as Kevin. How many passes did Mark complete?
Answer:
Kevin completed 36 passes during the season and Mark completed \(\frac{2}{9}\) of kevin’s amount.
So, Mark completed:
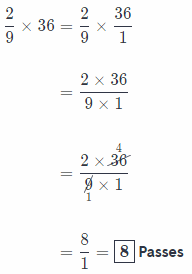
H.O.T. Focus On Higher Order Thinking
Question 17.
Represent Real-World Problems Kate wants to buy a new bicycle from a sporting goods store. The bicycle she wants normally sells for $360. The store has a sale where all bicycles cost \(\frac{5}{6}\) of the regular price. What is the sale price of the bicycle?

Answer:
As original price of bicycle is $360, \(\frac{5}{6}\) of the price would be:
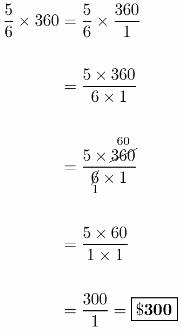
Discounted price would be $ 300
Division:
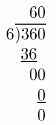
Question 18.
Error Analysis To find the product \(\frac{3}{7}\) × \(\frac{4}{9}\) Cameron simplified to \(\frac{3}{7}\) to \(\frac{1}{7}\) and then multiplied the fractions \(\frac{1}{7}\) and \(\frac{4}{9}\) to find the product \(\frac{4}{63}\). What is Cameron’s error?
Answer:
Cameron made a mistake in simplification process.
He simplified \(\frac{3}{7}\) into \(\frac{1}{7}\) which makes no sense.
When we simplify fractions, we divide both numerator and denominator by same number and get equivalent fraction to an original one!
For example, in this task he reached from \(\frac{3}{7}\) to \(\frac{1}{7}\), since we have same
denominators in both cases we can simply compare their numerators to see that they are not actually equal.
Let’s do it:
Number 3 is greater than 1, therefore, these fractions aren’t equivalent.
Question 19.
Justify Reasoning When multiplying a whole number by a fraction, the whole number is written as a fraction by placing the value of the whole number in the numerator and 1 in the denominator. Does this change the final answer? Explain why or why not.
Answer:
As we multiply a whole number by a fraction, we transform that whole number into fraction with 1 in denominator, that surely can not change our final answer. Why?
The answer is pretty simple actually. Remember what they have taught you in lower grades
Dividing some number by 1 does not change it, same is with multiplying!
Since fraction represent “division” of the numerator by denominator, we got our answer.