Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 15.3 Answer Key Relationships Between Sides and Angles in a Triangle.
Texas Go Math Grade 6 Lesson 15.3 Answer Key Relationships Between Sides and Angles in a Triangle
Essential Question
How can you use the relationships between side lengths and angle measures in a triangle to solve problems?
Texas Go Math Grade 6 Lesson 15.3 Explore Activity Answer Key
Explore Activity
Exploring the Relationship Between Sides and Angles in a Triangle
There is a special relationship between the lengths of sides and the measures of angles in a triangle.
A. Use geometry software to make triangle ABC. Make ∠A the smallest angle.
B. Choose one vertex and drag it s0 that you lengthen the side of the triangle opposite angle A. Describe what happens to ∠A.
C. Drag the vertex to shorten the side opposite ∠B. What happens to ∠B?

D. Make several new triangles. In each case, note the locations of the longest and shortest sides in relation to the largest and smallest angles. Describe your results.
Your Turn
Question 1.
Triangle ABC has side lengths of 11, 16, and 19.
Match each side with its correct length.
AB = ___ AC = ____ BC = ____

Answer:
Determine the side lengths of the triangle.
AB = 16 opposite the mid size angle
AC = 19 opposite the largest angle
BC = 11 opposite the smallest angle
The side lengths of the triangle are AB = 16; AC = 19; and BC = 11.
Question 2.
Triangle ABC has angle measures of 45°, 58°, and 77°. Match each angle with its correct measure.
m∠A = ___ m∠B = __ m∠C = ___
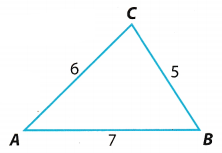
Answer:
Determine the angle measures of the triangle.
m∠A = 45 opposite the shortest side
m∠B = 58 opposite the midsize side
m∠C = 77 opposite the longest side
The angle measures of the triangle are ∠A = 45; ∠B = 58; and ∠C = 77
Your Turn
Question 3.
A fence around a rock garden is in the shape of a right triangle. Two angles measure 30° and 60°. Two sides measure 10 feet and 17.3 feet. The total length of the fence is 47.3 feet. How long is the side opposite the right angle? ______
Answer:
Determine the length of the opposite side of the right angle.
10 + 17.3 = 27.3 sum of the two side lengths
47.3 – 27.3 = 20 value of the third side length
a = 10 opposite the smallest angle
b = 17.3 opposite the midsize angle
c = 20 opposite the largest angle
The side length opposite to the right angle measures 20 feet.
Texas Go Math Grade 6 Lesson 15.3 Guided Practice Answer Key
Question 1.
Triangle ABC has side lengths of 17, 13, and 24. Match each side with its correct length. (Example 1)
____ = 24 ____ = 13 ____ = 17

Answer:
Determine the side of the triangle for each given measurement
AC = 24 opposite the largest angle
AB = 13 opposite the smallest angle
BC = 17 opposite the midsize angle
The sides of the triangle with the given measurements are:
AC = 24;
AB = 13;
BC = 17
Question 2.
The figure represents a traffic island that has angles measuring 60°, 20°, and 100°. Match each angle with its correct measure. (Example 1)
m∠___ = 100° m∠___ = 20° m∠___ = 60°
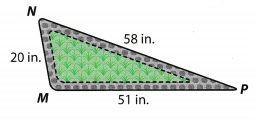
Answer:
Determine the angles of the triangle using its side lengths.
m∠M = 100° opposite the longest side
m∠P = 20° opposite the shortest side
m∠N = 60° opposite the midsize side
The angle measurements are: ∠M = 100°; ∠P = 20°; ∠N = 60°
Question 3.
Vocabulary Explain how the relationship between the sides and angles of a triangle applies to equilateral triangles. (Example 2)
Answer:
Equilateral triangle is a triangle with all sides equal and all angles equal. Therefore, the relationship between the angles and its sides will also be equal.
An equilateral triangle have equal angles and sides thus alt opposite sides of angles will have similar value.
Question 4.
Ramone is building a fence around a vegetable garden in his backyard. The fence will be in the shape of a right isosceles triangle. Two of the side measures are 12 feet and 16 feet. Use a problem solving model to find the total length of fencing he needs. Explain. (Example 2)
Answer:
Right isosceles triangle have two sides and two angles equal. The angle measures are 90° – 45° = 45°. If the opposite side of the largest angle measures 16 ft then the remaining two sides will measure 12 ft each. Add all the
side lengths to determine the total length of fencing he needs or the perimeter
P = 12 + 12 + 16 = 40 feet
The total length of fencing needed for the vegetable garden is 40 feet.
Essential Question Check-In
Question 5.
Describe the relationship between the lengths of the sides and the measures of the angles in a triangle.
Answer:
The relationship of sides and angles in a triangle are opposites The opposite of the largest angle is the longest side while the opposite of the smallest angle is the shortest side and the opposite of the midsize angle is the midsize side.
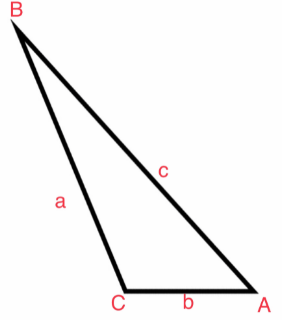
The longest side is opposite of the largest angle. The midsize side is opposite of the midsize angle. The shortest side is opposite of the smallest angle.
Texas Go Math Grade 6 Lesson 15.3 Independent Practice Answer Key
Use the figure for 6-8.
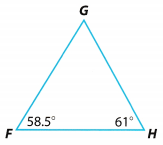
Question 6.
Critique Reasoning Dustin says that ΔFGH is an equilateral triangle because the sides appear to be the same length. Is his reasoning valid? Explain.
Answer:
An equilateral triangle has all sides and all angels equal. Based from the figure, the measure of ∠F = 58.5° and ∠H = 61° while the unknown angle is ∠G = 60.5. It shows that the angles have different measurements which
do not comprise an equilateral triangle having 60° angles. With the indicated measurements, it denotes that the side lengths of the triangle varies because of the different angle measurements.
It is not an equilateral triangle since the angles have different measurements then the side lengths will also have different measurements.
Question 7.
What additional information do you need to know before you can determine which side of the triangle is the longest? How can you find it?
Answer:
The additional information needed is the measure of the unknown angle to determine the longest side. In getting the measure of the unknown angle, add the given angles then subtract from 180°
Determine the measure of the unknown angle.
m∠F + m∠G + m∠H = 180° measures of each angle
58.5° + x + 61° = 180° substitute for the sum of angle measures in triangle
119.5° + x = 180° sum of the two angles
119.5° + x – 119.5° = 180° – 119.5° subtract 119.5° from both sides of the equation
x = 60.5° measure of the unknown angle
The largest angle is ∠H therefore, the longest side is side FG.
Question 8.
Which side of the triangle is the longest? Explain how you found the answer.
Answer:
Determine the longest side of the triangLe.
m∠F = 58. 5° = GH opposite the smallest angLe
m∠G = 60.5° = FH opposite the midsize angle
m∠H = 61° = FG opposite the largest angle
The longest side is the side opposite the largest angle which is side FG.
The figure shows the angle measurements formed by two fenced-in animal pens that share a side. Use the figure for 9-10.
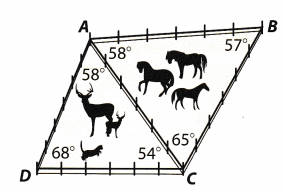
Question 9.
Caitlin says that \(\overline{A C}\) is the longest segment of fencing because it is opposite 68°, the largest angle measure in the figure. Is her reasoning valid? Explain.
Answer:
Her answer is invalid because her longest side of the triangle is only based on ∆ADC alone and not as a whole figure. By looking at the figure, it shows that there can still be other basis for the longest segment
The longest segment of the figure is not based on one triangle only
Question 10.
What is the longest segment of fencing in ΔABC? Explain your reasoning.
Answer:
Determine the longest segment of the ΔABC.
m∠4 = 58° = BC opposite the midsize angle
m∠B = 57° = AC opposite the smallest angle
m∠C = 65° = AB opposite the largest angle
Based on the concept of opposite angles, the longest segment of the indicated triangle is segment AB.
Question 11.
Find the longest segment of fencing in the figure. Explain your reasoning.
Answer:
Segment AC is the longest segment for the ΔADC white segment AB is the longest segment for ΔABC. Therefore, the longest segment of the whole figure is segment AB because segment AC is less than segment AB.
Segment AB
Question 12.
In triangle ABC, \(\overline{A B}\) is longer than \(\overline{B C}\) and \(\overline{B C}\) is longer than \(\overline{A C}\).
a. Draw a sketch of triangle ABC.
Answer:
Sketch of the triangle.
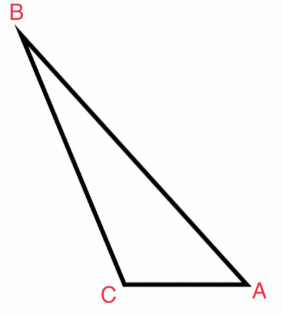
Triangle ABC has a longest side of segment AB, midsize side of segment BC, and shortest side of segment AC.
b. Name the smallest angle in the triangle. Explain your reasoning.
Answer:
Based from the figure, the smallest angle is ∠B because it is the opposite angle of the smallest side which is segment AC
The smallest angle is ∠B.
Texas Go Math Grade 6 Lesson 15.3 H.O.T. Focus On Higher Order Thinking Answer Key
Question 13.
Persevere in Problem Solving Determine the shortest line segment in the figure. Explain how you found the answer.
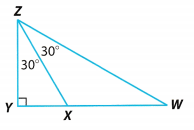
Answer:
The shortest line segment of the whole figure is segment ZY in reference to ∆WYZ.
m∠W = 30 = ZY opposite the smallest angle
m∠Y = 90 = WZ opposite the largest angle
m∠Z = 60 = WY opposite the midsize angle
Segment ZY is the shortest segment of the triangle.
Question 14.
Communicate Mathematical Ideas Explain how the relationship between the sides and angles of a triangle applies to isosceles triangles.
Answer:
An isosceles triangle has two sides of equal length. If two sides of an isosceles triangle have equal length, then the opposite angles of those two sides are also equal. Therefore, an isosceLes triangle has two equal sides and two equal angles.
Two sides of an isosceles triangle are equal therefore, two angles are also equal.
Question 15.
Critical Thinking Can a scalene triangle contain a pair of congruent angles? Explain.
Answer:
A scalene triangle has no equal sides. Knowing the relationship of the sides and its opposite angles, therefore it shows that a scalene triangle does not have equal angles. Thus, it also denotes that it cannot have a pair of congruent angles.
A scalene triangle cannot have a pair of congruent angles because all of its sides and angles are not equal.