Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 13.3 Answer Key Multiplication and Division Inequalities with Positive Numbers.
Texas Go Math Grade 6 Lesson 13.3 Answer Key Multiplication and Division Inequalities with Positive Numbers
Texas Go Math Grade 6 Lesson 13.3 Explore Activity Answer Key
Modeling One-Step Inequalities
You can use algebra tiles to solve inequalities that involve multiplying positive numbers.

Dominic is buying school supplies. He buys 3 binders and spends more than $9. How much did he spend on each binder?
A. Let x represent the cost of one binder. Write an inequality.
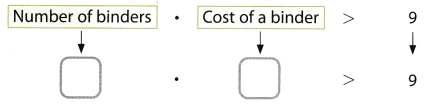
B. The model shows the inequality from A
There are _________ x-tiles, so draw circles to separate the tiles into ________ equal groups. _____________
How many units are in each group? _________
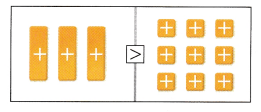
C. What values make the inequality you wrote in A true? Graph the solution of the inequality. _________
![]()
Reflect
Question 1.
Analyze Relationships Is 3.25 a solution of the inequality you wrote in A ? If so, does that solution make sense for the situation?
Answer:
Inequality for A is the following:
3 ∙ x > 9
We can substitute 3.2 for x and check if inequality is true, so we have the following:
3 ∙ 3.25 > 9
9 ∙ 75 > 9
We got that inequality is true, so, 3.25 can be the solution. And yes, this solution makes sense for the situation.
Question 2.
Represent Real-World Problems Rewrite the situation in A to represent the inequality 3x < 9.
Answer:
Modified situation which represents given inequality could be:
Dominic is buying school supplies. He buys 3 binders and spends less than 9$. How much did he spend on each binder?
Your Turn
Solve each inequality. Graph and check the solution.
Question 3.
5x ≥ 100

Answer:
First step in solving given inequality is dividing both sides by 5 and get:
\(\frac{5 x}{5} \geq \frac{100}{5}\)
x ≥ 20
Now, we will graph the solution:

We will check the solution by substituting a solution from the shaded part of the graph into the original inequality.
We will substitute 30 for x into the original inequality and get:
5 ∙ 30 ≥ 100
150 ≥ 100
So, the inequality is true
x ≥ 20
Question 4.
\(\frac{z}{4}\) < 11

Answer:
First step in solving given inequality is multiplying both sides by 4 and get:
4(\(\frac{z}{4}\)) < 11(4)
x < 44
Now, we will graph the solution:

We will check the solution by substituting a solution from the shaded part of the graph into the original inequality.
We will substitute 40 for x into the original inequality and get:
\(\frac{40}{4}\) < 11
10 < 11
So, the inequality is true.
z < 44
Reflect
Question 5.
Represent Real-World Problems Write and solve a real-world problem for the inequality 4x ≤ 60.
Answer:
Justin buys snacks. He bought 4 packs and spent $60 or less than $60. How much costs one pack of snacks?
Let x represent a price of one pack of snacks. According to given information.
we have the following inequality:
4x ≤ 60
In order to solve it. We will divide it by 4 and get:
\(\frac{4 x}{4} \leq \frac{60}{4}\)
x ≤ 15
So, one pack of snacks costs $15 or less than $15.
Your Turn
Question 6.
A paperweight must weigh less than 4 ounces. Brittany wants to make 6 paperweights using sand. Write and solve an inequality to find the possible weight of the sand she needs.
Answer:
Let x represent the possible weight of the sand Brittany needs. According to all informations, we have the following inequality:
6x < 4
We will, divide by 6 given inequality in order to solve previous inequality and get:
\(\frac{6x}{6}\) < \(\frac{4}{6}\)
x < \(\frac{2}{3}\)
So, the weight of the sand must be less than \(\frac{2}{3}\) ounce.
We will check solution substituting \(\frac{1}{3}\) for x in original inequality and get:
6 ∙ \(\frac{1}{3}\) < 4
2 < 4
So, the inequality is true.
x < \(\frac{2}{3}\)
Texas Go Math Grade 6 Lesson 13.3 Guided Practice Answer Key
Question 1.
Write the inequality shown on the model. Circle groups of tiles to show the solution. Then write the solution. (Explore Activity)
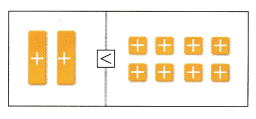
Inequality: ___________
Solution: ___________
Answer:
Solve each inequality. Graph and check the solution. (Example 1)
Question 2.
8y < 320 _________
![]()
Answer:
First step ¡s multiplying both sides by 8 and get:
\(\frac{8y}{8}\) < \(\frac{320}{80}\)
y < 40
Now, we will graph the solution:
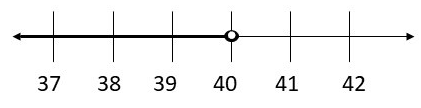
We will now check the solution by substituting a solution from the shaded part of graph into the original inequality.
We will substitute 30 for y into original inequality and get:
8 ∙ 30 < 320
240 < 320
So, the inequality is true.
y < 40
Question 3.
\(\frac{r}{3}\) ≥ 11 __________
![]()
Answer:
First we will multiply both sides by 3 and get:
3(\(\frac{r}{3}\)) ≥ 11 ∙ 3
r ≥ 33
Now, we will graph the solution:
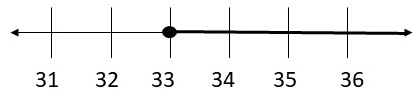
We will now check the solution by substituting a solution from the shaded part of graph into the original inequality.
We will substitute 39 for r into original inequality and get:
\(\frac{39}{3}\) ≥ 11
13 ≥ 11
So, the inequality is true.
r ≥ 33
Question 4.
Karen divided her books and put them on 6 shelves. There were at least 14 books on each shelf. How many books did she have? Write and solve an inequality to represent this situation. (Example 2)
Answer:
Let x represent number of books Karen had. According to previous informations, we need to solve following inequality:
\(\frac{x}{6}\) > 14
First, we will multiply by 6 both sides and get:
6(\(\frac{x}{6}\)) > 14.6
x > 84
Next thing we will do is to check the solution by substituting a value in the solution set in the original inequality.
We will substitute 90 for x and get:
\(\frac{90}{6}\) > 14
15 > 14
So, the inequality is true.
Conclusion is that Karen had at least 84 book.
x > 84
Essential Question Check-In
Question 5.
Explain how to solve and check the solution to 5x < 40 using properties of inequalities.
Answer:
In order to solve this inequality, we need to divide both sides by 5 and get:
\(\frac{5x}{5}\) < \(\frac{40}{5}\)
x < 8
So, we got that set of solutions is x < 8. Now we will check the solution by substituting a value in the solution set in the original inequality. We will substitute 5 for x and get:
5 ∙ 5 < 40
25 < 40
So, the inequality is true.
Texas Go Math Grade 6 Lesson 13.3 Independent Practice Answer Key
Write and solve an inequality for each problem.
Question 6.
Geometry The perimeter of a regular hexagon is at most 42 inches. Find the possible side lengths of the hexagon.
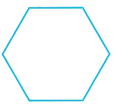
Answer:
We can notice that hexagon has 6 sides, so, let x be length of one side of hexagon. Because this is a regular hexagon, all sides have equal lengths. The perimeter is calculated by multiplying side length by 6, so, according to given informations in this task, we get the following inequality:
6x ≤ 42
In order to solve this inequality, we will divide both sides by 6 and get:
\(\frac{6x}{6}\) ≤ \(\frac{42}{6}\)
x ≤ 7
So, the possible length of side of the hexagon ¡s at most 7.
Question 7.
Tamar needs to make at least $84 at work on Tuesday to afford dinner and a movie on Wednesday night. She makes $14 an hour at her job. How many hours does she need to work on Tuesday?
Answer:
Let x represent number of hours Tamara needs to work on Tuesday.
According to all information in the task, we have the following inequality:
14x ≥ 84
In order to solve this inequality, we need to divide both sides by 14 and get:
\(\frac{14x}{14}\) ≥ \(\frac{84}{14}\)
x ≥ 6
So, Tamara needs to work at least 6 hours on Tuesday
Question 8.
In a litter of 7 kittens, each kitten weighs more than 3.5 ounces. Find the possible total weight of the litter.
Answer:
Let x represent the possible total. weight of the litter.
According to all informations in the task, we have the following inequality:
\(\frac{x}{7}\) > 3.5
We will multiply both sides by 7 and get:
7(\(\frac{x}{7}\)) > 3.5 ∙ 7
x > 24.5
So, the possible total weight of the litter is more than 24.5 ounces.
Question 9.
To cover his rectangular backyard, Will needs at least 1 70.5 square feet of sod. The length of Will’s yard is 15.5 feet. What are the possible widths of Will’s yard?
Answer:
Let x represent width of Will’s yard. In order to calculate it, we need to solve the following inequality:
15.5x ≥ 170.5
We wiLl divide both sides by 15.5 and get:
\(\frac{15.5x}{15.5}\) ≥ \(\frac{170.5}{15.5}\)
x ≥ 11
So, the width of Will’s yard need to be at least 11 feet.
Solve each inequality. Graph and check the solution.
Question 10.
10x ≤ 60
![]()
Answer:
First step is to divide both sides by 10, so, we get:
\(\frac{10x}{10}\) ≤ \(\frac{60}{10}\)
x ≤ 6
Now, we wilt graph the solution:

We will, now check the solution by substituting a solution from the shaded part of graph into the original inequality.
We will, substitute 3 for z into original inequality and get:
10 ∙ 3 ≤ 60
30 ≤ 60
So, the inequality is true.
x ≤ 6
Question 11.
\(\frac{t}{2}\) > 0
![]()
Answer:
First step is to multiply both sides by 2, so, we get:
2(\(\frac{t}{2}\)) > 0 ∙ 2
t > 0
Now, we will graph the solution:

We will now check the solution by substituting a solution from the shaded part of graph into the original inequality.
We will substitute 2 for t into original inequality and get:
\(\frac{2}{2}\) > 0
1 < 0 So, the inequality is true t > o
Question 12.
Steve pays less than $32 per day to rent his apartment. August has 31 days. What are the possible amounts Steve could pay for rent in August?
Answer:
Let x represent the possible amount Steve could pay for rent in August According to all informations, we have the following inequality we need to solve:
\(\frac{x}{31}\) < 32
We will multiply both sides by 31 and get:
31(\(\frac{x}{31}\)) < 32 ∙ 31
x < 992
So, Steve could pay for amount in August less than 992$.
Question 13.
If you were to graph the solution for exercise 12, would all points on the graph make sense for the situation? Explain.
Answer:
No, points which make sense for the situation will be between 992 and 0. Points with negative values do not make sense for this a real-world situation.
Question 14.
Multistep Lina bought 4 smoothies at a health food store. The bill was less than $16.
a. Write and solve an inequality to represent the cost of each smoothie.
Answer:
Let x represent the cost of each smoothie. We need to soLve the following inequaLity in order to caLculate x.
4x < 16
We need to divide both sides by 4 and get:
\(\frac{4x}{4}\) < \(\frac{16}{4}\)
x < 4
So, the price of each smoothie in less than 4$.
b. What values make sense for this situation? Explain.
Answer:
Values that makes sense for this situation are between 4 and 0.
Because, no one sells nothing for price 0.
So only previous values make sense for this situation.
c. Graph the values that make sense for this situation on the number line.
Answer:
According to part (b), we will graph the values that make sense for this situation, it would be:

Solve each inequality.
Question 15.
\(\frac{p}{13}\) ≤ 30
Answer:
First step is to multiply both sides by 13:
13 (\(\frac{p}{13}\)) ≤ 30 ∙ 13
p ≤ 390
Now, we will graph the solution:
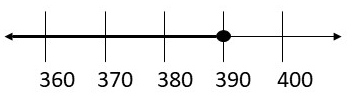
Next step is to check the solution by substituting a solution from the shaded part of the graph into the original inequality.
We will substitute 360 for p and get:
\(\frac{360}{13}\) ≤ 30
27.69 ≤ 30
So, the inequality is true
p ≤ 390
Question 16.
2t > 324
Answer:
First step is to divide both sides by 2, so, we have the following:
\(\frac{2t}{2}\) > \(\frac{324}{2}\)
t > 162
Now, we will graph the solution:
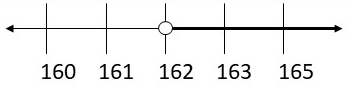
Next step is to check the solution by substituting a soLution from the shaded part of the graph into the original inequality.
We will substitute 170 for t and get:
2 ∙ 170 > 324
340 > 324
So, the inequality is true.
t > 162
Question 17.
12y ≥ 1
Answer:
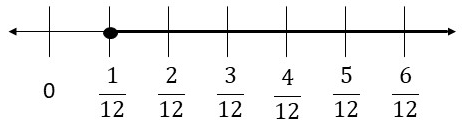
Next step is to check the solution by substituting a solution from the shaded part of the graph into the original inequality.
We will substitute 10 for y and get:
12 ∙ 10 ≥ 1
120 ≥ 1
So, the inequality is true.
y ≥ \(\frac{1}{12}\)
Question 18.
\(\frac{x}{9.5}\) < 11
Answer:
We will multiply both sides by 9.5 and get:
9.5 (\(\frac{x}{9.5}\)) < 11.9.5
x < 104.5
Now, we will graph the solution:
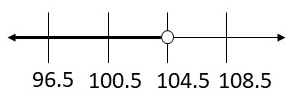
Next step is to check the solution by substituting a solution from the shaded part of the graph into the original inequality.
We will substitute 90 for x and get:
\(\frac{90}{9.5}\) < 11
9.47 < 11
So, the inequality is true.
x < 104.5
The sign shows some prices at a produce stand.
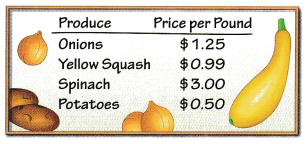
Question 19.
Tom has $10. What is the greatest amount of spinach he can buy?
Answer:
Let x represent the amount of spinach Tom can buy. According to all informations in the task, we have the following inequality:
3x ≤ 10
In order to solve this inequaLity, we need to divide both sides by 3 and get:
\(\frac{3x}{3}\) ≤ \(\frac{10}{3}\)
x ≤ 3.33
So, conclusion is that Tom can buy at most 3.33 pounds of spinach.
Question 20.
Gary has enough money to buy at most 5.5 pounds of potatoes. How much money does Gary have?
Answer:
Let x represent sum of money Gary have. According to data from the table and informations from task, we have the following inequality:
\(\frac{x}{0.50}\) ≤ 0.50
In order to solve this inequality, we need to multiply both sides by 0.50 and get:
0.50(\(\frac{x}{0.50}\)) ≤ 5.5 ∙ 0.50
x ≤ 2.75
So, conclusion is that Gary has at most 2.75.
Question 21.
Florence wants to spend no more than $3 on onions. Will she be able to buy 2.5 pounds of onions? Explain.
Answer:
Let x represent the amount of onions Florence can buy.
According to the table and informations, we get following inequality:
1.25x ≤ 3
In order to soLve this inequality, we need to divide both sides by 1.25 and get:
\(\frac{1.25 x}{1.25} \leq \frac{3}{1.25}\)
x ≤ 2.4
So, she can buy at most 2.4 pounds of onions. Conclusion is she can not buy 2.5 pounds of onions.
Question 22.
The produce buyer for a local restaurant wants to buy more than 30 lb of onions. The produce buyer at a local hotel buys exactly 12 pounds of spinach. Who spends more at the produce stand? Explain.
Answer:
Let x represent the sum of money the produce buyer for a local restaurant will spend for buying onions. So, we have the following inequality :
\(\frac{x}{1.25}\) > 30
In order to solve this inequality, we need to multiply both sides by 1.25 and get:
1.25(\(\frac{x}{1.25}\)) > 30 ∙ 1.25
x > 37.5
So, the produce buyer will spend more that $ 37.5 to by more than 30 lb of onions.
Now, let y represent sum of money the produce buyer for a local hotel will spend for buying exactly 12 pounds of spinach. We have the following equation we need to solve:
y ÷ 3 = 12
y = 12.3
y = 36
So, we can notice that the produce buyer will spend exactly $36 to buy 12 pounds of spinach.
Conclusion is that the produce buyer for a local restaurant will spend more money than the produce buyer for a local hotel.
H.O.T. Focus on Higher Order Thinking
Question 23.
Critique Reasoning A student solves \(\frac{r}{5}\) ≤ \(\frac{2}{5}\) and gets r ≤ \(\frac{2}{25}\) What is the correct solution? What mistake might the student have made?
Answer:
The mistake which student might made is that he divided by 5, not multiplied by 5
So, the right way to solve this inequality is to multiply by 5 and get:
5(\(\frac{r}{5}\)) ≤ \(\frac{2}{5}\) ∙ 5
r ≤ 2
So, the solution is r ≤ 2.
Question 24.
Represent Real-World Problems Write and solve a word problem that can be represented with 240 ≤ 2x.
Answer:
Mary want’s to spend $240 or more on buying chocolate as presents for guests at lier party. One pack costs $2, so, how many packs of chocolate she can buy?
Let x represent the number of packs of chocolate Mary can buy. According to all informations. we get the following inequality:
2x ≥ 240
We need to divide both sides by 2 and get:
\(\frac{2 x}{2} \geq \frac{240}{2}\)
x ≥ 120
So, she can at least buy 120 packs of chocolate or more.
Question 25.
Persevere in Problem Solving A rectangular prism has a length of 13 inches and a width of \(\frac{1}{2}\) inch. The volume of the prism is at most 65 cubic inches. Find all possible heights of the prism. Show your work.
Answer:
First, we will calculate the area of basis of this rectangular prism multiplying the length by the width and get:
B = 13 ∙ \(\frac{1}{2}\) = \(\frac{13}{2}\)
So, the area of bassis of rectangular prism is \(\frac{13}{2}\) square inches. Formula for calculating the volume is:
V = B ∙ H
Where V is the volume, B is the area of basis and H is its height.
According to all informations in the task, we have the following inequality we need to solve to find all possible heights of prism, where x represent height:
\(\frac{13}{2}\)x ≤ 65
We need to multiply both sides by \(\frac{2}{13}\) and get:
\(\frac{2}{13} \cdot \frac{13}{2} x \leq \frac{65}{1} \cdot \frac{2}{13}\)
x ≤ 10
So, the height of the prism can be at most 10 inches.