Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Review Test Answer Key Part 2.
Texas Go Math Grade 5 Review Test Answer Key Part 2
Selected Response
Question 1.
Charles bought \(\frac{7}{8}\) foot of electrical wire and \(\frac{5}{6}\) foot of copper wire for his science project. What is the least common denominator of the fractions?
(A) 14
(B) 18
(C) 24
(D) 48
Answer:
(C) 24
Explanation:
In fraction \(\frac{7}{8}\) denominator is 8 and in fraction \(\frac{5}{6}\) denominator is 6.
The least common denominator of those fractions is the least common multiple of denominators in those two fractions.
So, in this case it would be 24
Question 2.
Tom jogged \(\frac{3}{5}\) mile on Monday and \(\frac{2}{6}\) mile on Tuesday. How much farther did Tom jog on Monday than on Tuesday?
(A) \(\frac{1}{30}\) mile
(B) \(\frac{3}{15}\) mile
(C) \(\frac{8}{30}\) mile
(D) \(\frac{14}{15}\) mile
Answer:
(C) \(\frac{8}{30}\) mile
Explanation:
In order to find how much farther Tom jogged on Monday than to Tuesday, we need to subtract \(\frac{2}{6}\) from \(\frac{3}{5}\). The least common denominator of those two fractions is 30, so, we get:
\(\frac{3}{5}\) – \(\frac{2}{6}\) = \(\frac{3 \cdot 6-2 \cdot 5}{30}\) = \(\frac{8}{30}\)
Conclusion is that correct answer is C.
Question 3.
Three fences on a ranch measure \(\frac{15}{16}\) mile, \(\frac{7}{8}\) mile, and \(\frac{7}{16}\) mile. Which is the best estimate of the total length of all three fences?
(A) 1\(\frac{1}{2}\) miles
(B) 1\(\frac{3}{4}\) miles
(C) 2\(\frac{1}{2}\) miles
(D) 3 miles
Answer:
(C) 2\(\frac{1}{2}\) miles
Explanation:
We need to sum those three fractions. The Least common denominator for those fractions is 16, so, we get:
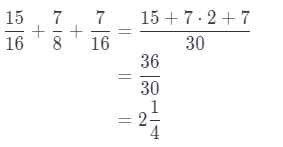
So, we can see that the best estimate of the total length of all three fences is 2\(\frac{1}{2}\) miles, or C.
Question 4.
Lawrence bought \(\frac{3}{4}\) pound of roast beef. He used \(\frac{1}{4}\) pound to make a sandwich. How much roast beef remained after Lawrence made his sandwich?
(A) \(\frac{1}{4}\)pound
(B) \(\frac{1}{3}\) pound
(C) \(\frac{1}{2}\) pound
(D) 3 pounds
Answer:
(C) \(\frac{1}{2}\) pound
Explanation:
In order to find how much roast beef remained after Lowrence made his sandwich we need to subtract those two fractions. So, we get:
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\)
= \(\frac{1}{2}\)
Conclusion is that correct answer is C, \(\frac{1}{2}\) pound roast beef remained.
Question 5.
A pizza box measures 16 inches by 16 inches by 2 inches. What is the volume of the box?
(A) 128 cubic inches
(B) 256 cubic inches
(C) 512 cubic inches
(D) 640 cubic inches
Answer:
(C) 512 cubic inches
Explanation:
The volume of those kind of box we calculate multiplying all three measures of sides. So, the volume of this box:
16 ∙ 16 ∙ 2 = 512 cubic inches.
Conclusion is that correct answer is C.
Question 6.
Vanessa made 6 sandwiches for a party and cut them all into fourths. How many \(\frac{1}{4}\) -sandwich pieces did she have?
(A) 1\(\frac{1}{2}\)
(B) 2\(\frac{1}{4}\)
(C) 4
(D) 24
Answer:
(A) 1\(\frac{1}{2}\)
Explanation:
In order to find how many \(\frac{1}{4}\) -sandwich pieces she have to multiply 6 by \(\frac{1}{4}\). so, we get the folowing:
6 ∙ \(\frac{1}{4}\) = \(\frac{6}{4}\)
= \(\frac{3}{2}\)
= 1\(\frac{1}{2}\)
So, correct answer is A.
Question 7.
Dr. Watson combines 400 mL of detergent, 800 mL of alcohol, and 1,500 mL of water. How many liters of solution does he have?
(A) 2.7 liters
(B) 27 liters
(C) 270 liters
(D) 2,700 liters
Answer:
(A) 2.7 liters
Explanation:
In order to find how many liters of solution he has we need to sum following:
400 + 800 + 1500 = 2700 ml
Because 1 L = 1000 mL, conclusion is that 2700 mL = 2.7L, so, Dr. Watson has 2.7 L of solution.
Correct answer is A.
Question 8.
Give the most descriptive name for the figure.
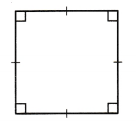
(A) square
(B) rectangle
(C) parallelogram
(D) rhombus
Answer:
(A) square
Explanation:
From picture, as much as we can see, the most descriptive name for the figure would be square.
It is square, because it has all four sides with the same measures.
Question 9.
Find the volume of the rectangular prism. 5 cm,
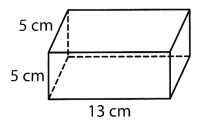
(A) 23 cm3
(B) 184 cm3
(C) 310 cm3
(D) 325 cm3
Answer:
(D) 325 cm3
Explanation:
Volume of this rectangular prism is product of measures of all three sides, so, we have following:
V = 13 ∙ 5 ∙ 5 = 325 cm3
So, correct answer is D.
Question 10.
Which ordered pair describes the location of Point A?
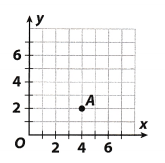
(A) (0, 2)
(B) (2, 4)
(C) (4, 0)
(D) (4, 2)
Answer:
(D) (4, 2)
Explanation:
From picture we can see that for point A corresponding on the x-axis is 4 and corresponding value on the y-axis is 2, so, it would be point (4, 2),
Question 11.
Which ordered pair describes the location of Point B?
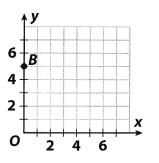
(A) (0, 5)
(B) (5, 0)
(C) (5, 5)
(D) (1, 5)
Answer:
(A) (0, 5)
Explanation:
From picture we can see that for point B corresponding value on the x-axis is 0 and corresponding value on y axis is 5, so, it would be pair (0, 5).
Question 12.
Which set of ordered pairs was generated by the equation y = x + 5?
(A) (1, 5), (2, 10), (3, 15), (4, 20)
(B) (3, 8), (4, 9), (6, 11), (8, 13)
(C) (2, 11), (4, 16), (5, 21)
(D) (1, 5), (3, 5), (4, 5), (7, 5)
Answer:
(B) (3, 8), (4, 9), (6, 11), (8, 13)
Explanation:
Form given equation we can see that y value is for 5 greater than the value of x. The only one set of ordered pairs which is generated by given equation is B. Really:
8 = 3 + 5,
9 = 4 + 5,
11 = 6 + 5,
13 = 8 + 5
Question 13.
Gina wants to ship three books that weigh 2\(\frac{7}{16}\) pounds, 1\(\frac{7}{8}\) pounds and \(\frac{1}{2}\) pound. Which is the best estimate for the total weight of the three books?
(A) 3\(\frac{1}{2}\) pounds
(B) 4 pounds
(C) 5 pounds
(D) 6 pounds
Answer:
(C) 5 pounds
Explanation:
First, those weights in pounds we need to be fractions, so, we have the following:
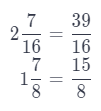
Because now we have fractions \(\frac{39}{16}\), \(\frac{15}{8}\) and \(\frac{1}{2}\), we have to add them in order to find their sum and the best estimate for the total weight of those three books.
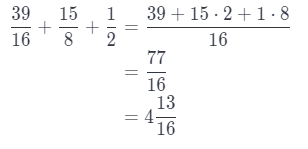
Conclusion is the best estimate is 5 pounds.
Question 14.
How much trail mix will each person get if 5 people share \(\frac{1}{2}\) pound of trail mix?
(A) \(\frac{1}{10}\) pound
(B) \(\frac{1}{5}\) pounds
(C) 2\(\frac{1}{2}\) pound
(D) 10 pounds
Answer:
(A) \(\frac{1}{10}\) pound
Explanation:
If 5 people share \(\frac{1}{2}\) pound of trait mix, each person will get \(\frac{1}{10}\) pound, because:
\(\frac{1}{2}\) ÷ 5 = \(\frac{1}{2}\) ∙ \(\frac{1}{5}\)
= \(\frac{1}{10}\)
Question 15.
Each cube in the solid figure represents one cubic centimeter. What is the volume in cubic centimeters of the solid?
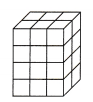
(A) 24 cubic centimeters
(B) 48 cubic centimeters
(C) 72 cubic centimeters
(D) 96 cubic centimeters
Answer:
(A) 24 cubic centimeters
Explanation:
One side of the solid has three cubes, so, measure of that side is 3 centimeters. Other side of the solid has two cubes, so, its measure is 2 centimeters And the third side has four cubes, so, its measure is 4 centimeters.
Volume of this solid is product of measures of all three sides, so, we have following:
y = 3 ∙ 2 ∙ 4 = 24
So, its volume is 24 cubic centimeters.
Gridded Response
Question 16.
It took Ray 0.45 hour to rake the leaves and \(\frac{3}{4}\) hour to mow the lawn. How many minutes did it take him to do both tasks?
Answer:
0.45 hours is 0.45 ∙ 60 = 27 minutes.
\(\frac{3}{4}\) hours is \(\frac{3}{4}\) ∙ 60 = 45 minutes.
So, Ray took 27 + 45 = 72 minutes to take the leaves.