Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 5.6 Answer Key Add and Subtract Mixed Numbers.
Texas Go Math Grade 5 Lesson 5.6 Answer Key Add and Subtract Mixed Numbers
Unlock the Problem
Denise mixed 1\(\frac{4}{5}\) ounces of blue paint with 2\(\frac{1}{10}\) ounces of yellow paint. How many ounces of paint did Denise mix?
- What operation should you use to solve the problem?
- Do the fractions have the same denominator?
Add. 1\(\frac{4}{5}\) + 2\(\frac{1}{10}\)
To find the sum of mixed numbers with unequal denominators, you can use a common denominator.
STEP 1: Estimate the sum.
STEP 2: Find a common denominator. Use the common denominator to write equivalent fractions with equal denominators.
STEP 3: Add the fractions. Then add the whole numbers. Write the answer in simplest form.
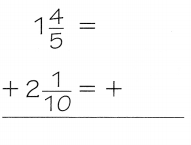
So, Denise mixed __________ ounces of paint.
Answer:
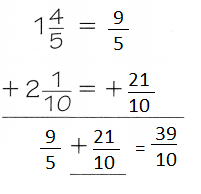
So, Denise mixed \(\frac{39}{10}\) ounces of paint.
Math Talk
Mathematical Processes
Did you use the least common denominator? Explain.
Answer: yes
Explanation:
The sum of mixed numbers with unequal denominators can use a common denominator.
Question 1.
Explain how you know whether your answer is reasonable.
Answer: Yes my answer is reasonable
Because, the sum of two mixed numbers is solved and it is proved
Question 2.
What other common denominator could you have used?
Answer: 50
multiply 5 x 10 = 50
Example
Subtract. 4\(\frac{5}{6}\) – 2\(\frac{3}{4}\)
You can also use a common denominator to find the difference of mixed numbers with unequal denominators.
STEP 1: Estimate the difference.
STEP 2: Find a common denominator. Use the common denominator to write equivalent fractions with equal denominators.
STEP 3: Subtract the fractions. Subtract the whole numbers. Write the answer in simplest form.

Answer:
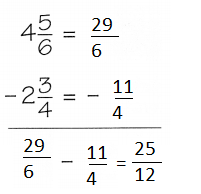
Question 3.
Explain how you know whether your answer is reasonable.
Answer: Used the common denominator to write equivalent fractions with equal denominators.
so, my answer is reasonable.
Share and Show
Question 1.
Use a common denominator to write equivalent fractions with equal denominators and then find the sum. Write your answer in simplest form.
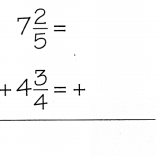
Answer:
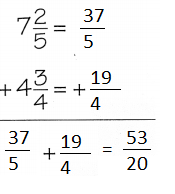
Explanation:
Used a common denominator and written equivalent fractions with equal denominators and then find the sum. written the answer in simplest form.
Find the sum. Write your answer in simplest form.
Question 2.
2\(\frac{3}{4}\) + 3\(\frac{3}{10}\)
Answer:
2\(\frac{3}{4}\) + 3\(\frac{3}{10}\) = \(\frac{11}{4}\) + \(\frac{33}{10}\) = \(\frac{55}{20}\) + \(\frac{66}{20}\) = \(\frac{121}{20}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 3.
5\(\frac{3}{4}\) + 1\(\frac{1}{3}\)
Answer:
5\(\frac{3}{4}\) + 1\(\frac{1}{3}\) = \(\frac{23}{4}\) + \(\frac{4}{3}\) = \(\frac{69}{12}\)+ \(\frac{16}{12}\) = \(\frac{85}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 4.
3\(\frac{4}{5}\) + 2\(\frac{3}{10}\)
Answer:
3\(\frac{4}{5}\) + 2\(\frac{3}{10}\) = \(\frac{19}{5}\) + \(\frac{23}{10}\) = \(\frac{38}{10}\) + \(\frac{23}{10}\) = \(\frac{61}{10}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Problem Solving
Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.
Question 5.
1\(\frac{5}{12}\) + 4\(\frac{1}{6}\)
Answer:
1\(\frac{5}{12}\) + 4\(\frac{1}{6}\) = \(\frac{17}{12}\) + \(\frac{21}{6}\) = \(\frac{17}{12}\) + \(\frac{42}{12}\) = \(\frac{59}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 6.
8\(\frac{1}{2}\) + 6\(\frac{3}{5}\)
Answer:
8\(\frac{1}{2}\) + 6\(\frac{3}{5}\) = \(\frac{17}{2}\) + \(\frac{33}{5}\) = \(\frac{85}{10}\) + \(\frac{66}{10}\) = \(\frac{151}{10}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 7.
2\(\frac{1}{6}\) + 4\(\frac{5}{9}\)
Answer:
2\(\frac{1}{6}\) + 4\(\frac{5}{9}\) = \(\frac{13}{6}\) + \(\frac{36}{9}\) = \(\frac{39}{18}\) + \(\frac{72}{18}\) = \(\frac{41}{18}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 8.
3\(\frac{5}{8}\) + \(\frac{5}{12}\)
Answer:
3\(\frac{5}{8}\) + \(\frac{5}{12}\) = \(\frac{29}{8}\) + \(\frac{5}{12}\) = \(\frac{87}{24}\) + \(\frac{10}{24}\) = \(\frac{97}{24}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 9.
3\(\frac{2}{3}\) – 1\(\frac{1}{6}\)
Answer:
3\(\frac{2}{3}\) – 1\(\frac{1}{6}\) = \(\frac{11}{3}\) – \(\frac{7}{6}\) = \(\frac{22}{6}\) – \(\frac{7}{6}\) = \(\frac{15}{6}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 10.
5\(\frac{6}{7}\) – 1\(\frac{2}{3}\)
Answer:
5\(\frac{6}{7}\) – 1\(\frac{2}{3}\) = \(\frac{41}{7}\) – \(\frac{5}{3}\) = \(\frac{123}{21}\) – \(\frac{35}{21}\) = \(\frac{88}{21}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 11.
2\(\frac{7}{8}\) – \(\frac{1}{2}\)
Answer:
2\(\frac{7}{8}\) – \(\frac{1}{2}\) = \(\frac{23}{8}\) – \(\frac{1}{2}\) = \(\frac{23}{8}\) – \(\frac{4}{8}\) = \(\frac{19}{8}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 12.
4\(\frac{7}{12}\) – 1\(\frac{2}{9}\)
Answer:
4\(\frac{7}{12}\) – 1\(\frac{2}{9}\) = \(\frac{55}{12}\) – \(\frac{7}{5}\) = \(\frac{275}{60}\) – \(\frac{72}{60}\) = \(\frac{203}{60}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 13.
Communicate Why do you need to write equivalent fractions with common denominators to add 4\(\frac{5}{6}\) and \(\frac{11}{8}\)? Explain.
Answer: 4\(\frac{5}{6}\) + \(\frac{11}{8}\) = \(\frac{25}{24}\) + \(\frac{11}{24}\) = \(\frac{36}{24}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Problem Solving
Use the table to solve 14-15.

Question 14.
H.O.T. Multi-Step Gavin needs to make 2 batches of Mango paint. Explain how you could find the total amount of paint Gavin mixed.
Answer: \(\frac{70}{6}\)
Explanation:
Gavin needs to make 2 batches of Mango paint
5\(\frac{5}{6}\) red + 5\(\frac{5}{6}\) yellow = \(\frac{70}{6}\) mango
Question 15.
H.O.T. Gavin mixes the amount of red from one shade of paint with the amount of yellow from a different shade of paint. He mixes the batch so he will have the greatest possible amount of paint. What amounts of red and yellow from which shades are used in the mixture? Explain your answer.

Answer: The amounts of red and yellow from each shades are used in the mixture is same
Explanation:
Gavin needs to make 2 batches of Mango paint
5\(\frac{5}{6}\) red + 5\(\frac{5}{6}\) yellow = \(\frac{70}{6}\) mango
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 16.
Dr. Whether-or-Not collects two hailstones during a storm in California. One hailstone weighs 2\(\frac{3}{8}\) pounds, and the other hailstone weighs 1\(\frac{3}{10}\) pounds. How much heavier is the larger hailstone than the smaller hailstone?
(A) \(\frac{3}{40}\) pounds
(B) 1\(\frac{27}{40}\) pounds
(C) 1\(\frac{3}{40}\) pounds
(D) 3\(\frac{27}{40}\) pounds
Answer: D
Explanation:
Dr. Whether-or-Not collects two hailstones during a storm in California.
One hailstone weighs 2\(\frac{3}{8}\) pounds,
and the other hailstone weighs 1\(\frac{3}{10}\) pounds.
2\(\frac{3}{8}\) + 1\(\frac{3}{10}\) pounds
\(\frac{19}{8}\) + \(\frac{13}{10}\)
\(\frac{294}{80}\)
3\(\frac{27}{40}\) pounds
Question 17.
Apply Jason is making a fruit salad. He mixes in 3\(\frac{1}{4}\) cups of orange melon and 2\(\frac{2}{3}\) cups of green melon. How many cups of melon does Jason put in the fruit salad?
(A) 5\(\frac{1}{4}\) cups
(B) 5\(\frac{1}{3}\) cups
(C) 5\(\frac{7}{12}\) cups
(D) 5\(\frac{11}{12}\) cups
Answer: A
Explanation:
Apply Jason is making a fruit salad.
He mixes in 3\(\frac{1}{4}\) cups of orange melon and 2\(\frac{2}{3}\) cups of green melon.
3\(\frac{1}{4}\) + 2\(\frac{2}{3}\)
\(\frac{13}{4}\) + \(\frac{8}{3}\)
\(\frac{39}{12}\) + \(\frac{24}{12}\)
\(\frac{63}{12}\)
5\(\frac{1}{4}\)
Question 18.
Multi-Step Dakota makes a salad dressing by combining 6\(\frac{1}{3}\) fluid ounces of oil and 2\(\frac{3}{8}\) fluid ounces of vinegar in a jar. She then pours 2\(\frac{1}{4}\) fluid ounces of the dressing onto her salad. How much dressing remains in the jar?
(A) 6\(\frac{1}{8}\) fluid ounces
(B) 6\(\frac{3}{8}\) fluid ounces
(C) 6\(\frac{11}{24}\) fluid ounces
(D) 6\(\frac{17}{24}\) fluid ounces
Answer: C
Dakota makes a salad dressing by combining 6\(\frac{1}{3}\) fluid ounces of oil
and 2\(\frac{3}{8}\) fluid ounces of vinegar in a jar.
She then pours 2\(\frac{1}{4}\) fluid ounces of the dressing onto her salad.
6\(\frac{1}{3}\) + 2\(\frac{3}{8}\) – 2\(\frac{1}{4}\)
\(\frac{155}{24}\)
6\(\frac{11}{24}\) fluid ounces
Texas Test Prep
Question 19.
Yolanda walked 3\(\frac{6}{10}\) miles. Then she walked 4\(\frac{1}{2}\) more miles. How many miles did Yolanda walk?
(A) 7\(\frac{1}{10}\) miles
(B) 8\(\frac{7}{10}\) miles
(C) 8\(\frac{1}{10}\) miles
(D) 7\(\frac{7}{10}\) miles
Answer: C
Explanation:
Yolanda walked 3\(\frac{6}{10}\) miles.
Then she walked 4\(\frac{1}{2}\) more miles
3\(\frac{6}{10}\) + 4\(\frac{1}{2}\)
\(\frac{72}{20}\) + \(\frac{90}{20}\)
\(\frac{162}{20}\)
Texas Go Math Grade 5 Lesson 5.6 Homework and Practice Answer Key
Find the sum or difference. Write your answer in simplest form.
Question 1.
1\(\frac{1}{4}\) + 2\(\frac{2}{3}\) _____________
Answer:
1\(\frac{1}{4}\) + 2\(\frac{2}{3}\) = \(\frac{5}{4}\) + \(\frac{8}{3}\) = \(\frac{15}{12}\) + \(\frac{32}{12}\) = \(\frac{47}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 2.
3\(\frac{3}{4}\) + 4\(\frac{5}{12}\) _____________
Answer:
3\(\frac{3}{4}\) + 4\(\frac{5}{12}\) = \(\frac{36}{12}\) + \(\frac{53}{12}\) = \(\frac{89}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 3.
1\(\frac{1}{3}\) + 2\(\frac{1}{6}\) _____________
Answer:
1\(\frac{1}{3}\) + 2\(\frac{1}{6}\) = \(\frac{8}{6}\) + \(\frac{13}{6}\) = \(\frac{21}{6}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 4.
4\(\frac{1}{2}\) + 3\(\frac{4}{5}\) _____________
Answer:
4\(\frac{1}{2}\) + 3\(\frac{4}{5}\) = \(\frac{45}{10}\) + \(\frac{38}{10}\) = \(\frac{83}{10}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 5.
5\(\frac{5}{6}\) + 4\(\frac{2}{9}\) ____________
Answer:
5\(\frac{5}{6}\) + 4\(\frac{2}{9}\) = \(\frac{35}{6}\) + \(\frac{38}{9}\) = \(\frac{105}{18}\) + \(\frac{76}{18}\) = \(\frac{181}{18}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 6.
7\(\frac{1}{4}\) + 3\(\frac{2}{5}\) ___________
Answer:
7\(\frac{1}{4}\) + 3\(\frac{2}{5}\) = \(\frac{29}{4}\) + \(\frac{17}{5}\) = \(\frac{145}{20}\) + \(\frac{68}{20}\) = \(\frac{213}{20}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 7.
3\(\frac{2}{7}\) + 8\(\frac{1}{3}\) _____________
Answer:
3\(\frac{2}{7}\) + 8\(\frac{1}{3}\) = \(\frac{23}{7}\) + \(\frac{25}{3}\) = \(\frac{69}{21}\) + \(\frac{175}{21}\) = \(\frac{244}{21}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 8.
4\(\frac{3}{7}\) + 3\(\frac{1}{2}\) ____________
Answer:
4\(\frac{3}{7}\) + 3\(\frac{1}{2}\) = \(\frac{31}{7}\) + \(\frac{7}{2}\) = \(\frac{62}{14}\) + \(\frac{49}{14}\) = \(\frac{114}{14}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 9.
2\(\frac{4}{5}\) – 1\(\frac{1}{2}\) ____________
Answer:
2\(\frac{4}{5}\) – 1\(\frac{1}{2}\) = \(\frac{14}{5}\) – \(\frac{3}{2}\) = \(\frac{28}{10}\) – \(\frac{15}{10}\) = \(\frac{13}{10}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 10.
5\(\frac{3}{8}\) – 1\(\frac{1}{4}\) ____________
Answer:
5\(\frac{3}{8}\) – 1\(\frac{1}{4}\) = \(\frac{43}{8}\) – \(\frac{5}{4}\) = \(\frac{43}{8}\) – \(\frac{10}{8}\) = \(\frac{33}{8}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 11.
4\(\frac{1}{3}\) – 3\(\frac{1}{6}\) _____________
Answer:
4\(\frac{1}{3}\) – 3\(\frac{1}{6}\) = \(\frac{13}{3}\) – \(\frac{19}{6}\) = \(\frac{26}{6}\) – \(\frac{19}{6}\) = \(\frac{7}{6}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 12.
6\(\frac{5}{6}\) – 5\(\frac{7}{9}\) _____________
Answer:
6\(\frac{5}{6}\) – 5\(\frac{7}{9}\) = \(\frac{41}{6}\) – \(\frac{53}{9}\) = \(\frac{123}{18}\) – \(\frac{106}{18}\) = \(\frac{17}{18}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 13.
4\(\frac{1}{3}\) – 2\(\frac{1}{4}\) ____________
Answer:
4\(\frac{1}{3}\) – 2\(\frac{1}{4}\) = \(\frac{13}{3}\) – \(\frac{9}{4}\) = \(\frac{52}{12}\) – \(\frac{27}{12}\) = \(\frac{25}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 14.
3\(\frac{1}{4}\) – 1\(\frac{1}{6}\) _____________
Answer:
3\(\frac{1}{4}\) – 1\(\frac{1}{6}\) = \(\frac{13}{4}\) – \(\frac{7}{6}\) = \(\frac{39}{12}\) – \(\frac{14}{12}\) = \(\frac{25}{12}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 15.
6\(\frac{3}{4}\) – 2\(\frac{5}{16}\) _____________
Answer:
6\(\frac{3}{4}\) – 2\(\frac{5}{16}\) = \(\frac{23}{4}\) – \(\frac{37}{16}\)= \(\frac{92}{16}\) – \(\frac{37}{16}\) = \(\frac{55}{16}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 16.
7\(\frac{3}{5}\) – 2\(\frac{1}{4}\) _____________
Answer:
7\(\frac{3}{5}\) – 2\(\frac{1}{4}\) = \(\frac{38}{5}\) – \(\frac{9}{4}\) = \(\frac{152}{20}\) – \(\frac{45}{20}\) = \(\frac{107}{20}\)
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Question 17.
Use two mixed numbers to write an equation with a sum of 4\(\frac{1}{4}\).
Answer:
Explanation:
Step I: We add the whole numbers, separately. We change the mixed fractions into improper fractions.
Step II: To add fractions, we take least common denominators and change the fractions into like fractions.
Step III: We find the sum of the whole numbers and the fractions in the simplest form.
Problem Solving
Question 18.
Lucas says his twin baby brothers have a total weight of 15\(\frac{1}{8}\) pounds. Jackson weighs pounds, and Jeremy weighs 8\(\frac{7}{8}\) pounds. Explain how you can use estimation to tell if the total weight is reasonable.
Answer:
Question 19.
The gas tank in Rebecca’s old car held 14\(\frac{1}{5}\) gallons. The gas tank in Rebecca’s new car holds 18\(\frac{1}{2}\) gallons. How many more gallons will the tank in Rebecca’s new car hold than her old car?
Answer: 4\(\frac{3}{10}\)
Explanation:
18\(\frac{1}{2}\) – 14\(\frac{1}{5}\)
= 4\(\frac{3}{10}\)
Lesson Check
Fill in the bubble completely to show your answer.
Use the table for 20-21.
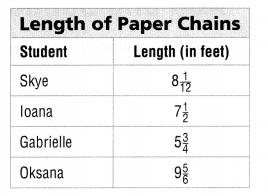
Four students made paper chains to decorate the community center. The table at the right shows the lengths of the paper chains.
Question 20.
If Ioana attaches her chain to the end of Gabrielle’s chain, what will be the length of the combined chain?
(A) 13\(\frac{3}{4}\) feet
(B) 13\(\frac{1}{4}\) feet
(C) 12\(\frac{1}{4}\) feet
(D) 12\(\frac{1}{2}\) feet
Answer: B
Explanation:
the length of the combined chain is 13\(\frac{1}{4}\) feet
7\(\frac{1}{2}\) feet + 5\(\frac{3}{4}\) feet=
\(\frac{30+23}{4}\) feet
\(\frac{53}{4}\)
Question 21.
How much longer is Oksana’s chain than Gabrielle’s chain?
(A) 15\(\frac{7}{12}\) feet
(B) 14\(\frac{1}{12}\) feet
(C) 4\(\frac{1}{4}\) feet
(D) 4\(\frac{1}{12}\) feet
Answer: D
4\(\frac{1}{12}\) feet is longer than Oksana’s chain than Gabrielle’s chain
Explanation:
9\(\frac{5}{6}\) feet + 5\(\frac{3}{4}\) feet=
\(\frac{118-69}{12}\) feet
\(\frac{49}{12}\)
4\(\frac{1}{12}\)
Question 22.
Mia hiked 2\(\frac{1}{2}\) miles farther than Jacob. Which could be the two distances each person hiked?
(A) Mia: 2\(\frac{1}{2}\) miles; Jacob: 1\(\frac{1}{4}\) miles
(B) Mia: 2\(\frac{1}{2}\) miles; Jacob: 7\(\frac{1}{2}\) miles
(C) Mia: 3\(\frac{2}{5}\) miles; Jacob: 5\(\frac{9}{10}\) miles
(D) Mia: 5\(\frac{9}{10}\) miles; Jacob: 3\(\frac{2}{5}\) miles
Answer: A
Explanation:
2\(\frac{1}{2}\) than jacob
if Mia: 2\(\frac{1}{2}\) miles; Jacob: 1\(\frac{1}{4}\) miles
Question 23.
Multi-Step Mr. Carter owned a ranch with 7\(\frac{1}{4}\) acres. Last year, he bought 3\(\frac{1}{5}\) acres of land from his neighbor. Then he sold 2\(\frac{1}{4}\) acres. How many acres does Mr. Carter own now?
(A) 10\(\frac{9}{20}\) acres
(B) 8\(\frac{1}{5}\) acres
(C) 12\(\frac{7}{10}\) acres
(D) 6\(\frac{3}{10}\) acres
Answer: B
Mr. Carter owned a ranch with 7\(\frac{1}{4}\) acres.
Last year, he bought 3\(\frac{1}{5}\) acres of land from his neighbor
Then he sold 2\(\frac{1}{4}\) acres.
7\(\frac{1}{4}\) + 3\(\frac{1}{5}\) – 2\(\frac{1}{4}\)
\(\frac{164}{20}\)
= 8\(\frac{1}{5}\) acres
Question 24.
Multi-Step This week, Maddie worked 2\(\frac{1}{2}\) hours on Monday, 2\(\frac{2}{3}\) hours on Tuesday, and 3\(\frac{1}{4}\) hours on Wednesday. How many more hours will Maddie need to work this week to make her goal of 10\(\frac{1}{2}\) hours a week?
(A) 2\(\frac{1}{12}\) hours
(B) 8\(\frac{5}{12}\) hours
(C) 18\(\frac{11}{12}\) hours
(D) 5\(\frac{1}{3}\) hours
Answer: A
Explanation:
This week, Maddie worked 2\(\frac{1}{2}\) hours on Monday,
2\(\frac{2}{3}\) hours on Tuesday,
and 3\(\frac{1}{4}\) hours on Wednesday.
2\(\frac{1}{2}\)+2\(\frac{2}{3}\) + 3\(\frac{1}{4}\) -10\(\frac{1}{2}\)
\(\frac{25}{12}\)
=2\(\frac{1}{12}\) hours