Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 5.5 Answer Key Add and Subtract Fractions.
Texas Go Math Grade 5 Lesson 5.5 Answer Key Add and Subtract Fractions
Unlock the Problem
Malia bought shell beads and glass beads to weave into designs in her baskets. She bought \(\frac{1}{4}\) pound of shell beads and \(\frac{3}{8}\) pound of glass beads. How many pounds of beads did she buy?
- Underline the question you need to answer.
- Draw a circle around the information you will use.
Add. \(\frac{1}{4}\) + \(\frac{3}{8}\). Write your answer in simplest form.
One Way
Find a common denominator by multiplying the denominators.
4 × 8 = ________ ← common denominator
Use the common denominator to write equivalent fractions with equal denominators. Then add, and write your answer in simplest form.
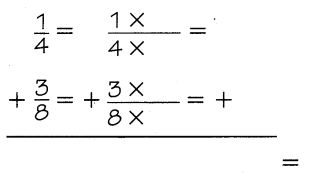
Another Way
Find the least common denominator.
The least common denominator of \(\frac{1}{4}\) and \(\frac{3}{8}\) is ___________.
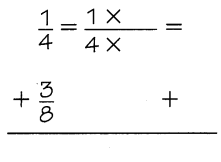
So, Malia bought _________ pound of beads.
Answer:
One Way
Find a common denominator by multiplying the denominators.
4 × 8 = 24 ← common denominator
Use the common denominator to write equivalent fractions with equal denominators. Then add, and write your answer in simplest form.
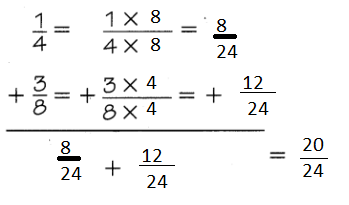
Another Way
The least common denominator of 14 and 38 is 8
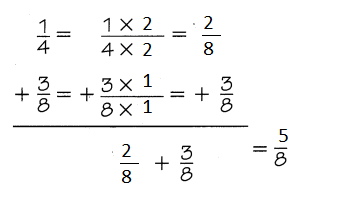
So, Malia bought \(\frac{5}{8}\) pound of beads.
Question 1.
Explain how you know whether your answer is reasonable.
Answer: The both methods are same
they both give the same answer
Least common denominator is the simplest method
Example
When subtracting two fractions with unequal denominators, follow the same steps you follow when adding two fractions. However, instead of adding the fractions, subtract.
Subtract. \(\frac{9}{10}\) – \(\frac{2}{5}\) Write your answer in simplest form.
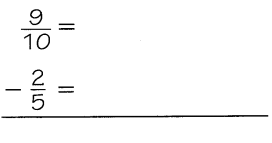
Describe the steps you took to solve the problem.
Answer:
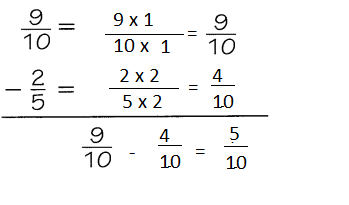
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 2.
Explain how you know whether your answer is reasonable.
Answer:
The fraction solved into simplest form is reasonable
which found by least common denominator
Share and Show
Find the sum or difference. Write your answer in simplest form.
Question 1.
\(\frac{5}{12}\) + \(\frac{1}{3}\)
Answer:
\(\frac{5}{12}\) + \(\frac{1}{3}\) = \(\frac{5}{12}\) + \(\frac{4}{12}\) = \(\frac{9}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 2.
\(\frac{2}{5}\) + \(\frac{3}{7}\)
Answer:
\(\frac{2}{5}\) + \(\frac{3}{7}\) = \(\frac{14}{35}\) + \(\frac{15}{35}\) =\(\frac{29}{35}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 3.
\(\frac{1}{6}\) + \(\frac{3}{4}\)
Answer:
\(\frac{1}{6}\) + \(\frac{3}{4}\) = \(\frac{2}{12}\) + \(\frac{9}{12}\) = \(\frac{11}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 4.
\(\frac{3}{4}\) – \(\frac{1}{8}\)
Answer:
\(\frac{3}{4}\) – \(\frac{1}{8}\) = \(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 5.
\(\frac{1}{4}\) – \(\frac{1}{7}\)
Answer:
\(\frac{1}{4}\) – \(\frac{1}{7}\) = \(\frac{7}{28}\) – \(\frac{4}{28}\)= \(\frac{3}{28}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 6.
\(\frac{9}{10}\) – \(\frac{1}{4}\)
Answer:
\(\frac{9}{10}\) – \(\frac{1}{4}\) = \(\frac{18}{20}\) – \(\frac{5}{20}\)= \(\frac{13}{20}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Math Talk
Mathematical Processes
Explain why it is important to check your answer for reasonableness.
Answer:
Problem Solving
Practice: Copy and Solve Find the sum or difference. Write your answer in simplest form.
Question 7.
\(\frac{1}{3}\) + \(\frac{4}{18}\)
Answer:
\(\frac{1}{3}\) + \(\frac{4}{18}\) = \(\frac{6}{18}\) + \(\frac{4}{18}\) =\(\frac{10}{18}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 8.
\(\frac{3}{5}\) + \(\frac{1}{3}\)
Answer:
\(\frac{3}{5}\) + \(\frac{1}{3}\) = \(\frac{9}{15}\) + \(\frac{5}{15}\) = \(\frac{14}{15}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 9.
\(\frac{3}{10}\) + \(\frac{1}{6}\)
Answer:
\(\frac{3}{10}\) + \(\frac{1}{6}\) = \(\frac{9}{30}\) + \(\frac{5}{30}\) = \(\frac{14}{30}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 10.
\(\frac{1}{2}\) + \(\frac{4}{9}\)
Answer:
\(\frac{1}{2}\) + \(\frac{4}{9}\) = \(\frac{9}{18}\) + \(\frac{8}{18}\) = \(\frac{17}{18}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 11.
\(\frac{1}{2}\) – \(\frac{3}{8}\)
Answer:
\(\frac{1}{2}\) – \(\frac{3}{8}\) = \(\frac{4}{8}\) – \(\frac{3}{8}\) = \(\frac{1}{8}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 12.
\(\frac{5}{7}\) – \(\frac{2}{3}\)
Answer:
\(\frac{5}{7}\) – \(\frac{2}{3}\) = \(\frac{15}{21}\) – \(\frac{14}{21}\) = \(\frac{1}{21}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 13.
\(\frac{4}{9}\) – \(\frac{1}{6}\)
Answer:
\(\frac{4}{9}\) – \(\frac{1}{6}\) = \(\frac{8}{18}\) – \(\frac{3}{18}\) = \(\frac{5}{18}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 14.
\(\frac{11}{12}\) – \(\frac{7}{15}\)
Answer:
\(\frac{11}{12}\) – \(\frac{7}{15}\) = \(\frac{55}{60}\) – \(\frac{28}{60}\) = \(\frac{27}{60}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
H.O.T. Algebra Find the unknown number.
Question 15.
\(\frac{9}{10}\) – ☐ = \(\frac{1}{5\)
☐ = ___________
Answer:
\(\frac{9}{10}\) – \(\frac{7}{10}\)= \(\frac{1}{5\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 16.
\(\frac{5}{12}\) + ☐ = \(\frac{1}{2}\)
☐ = ____________
Answer:
\(\frac{5}{12}\) + \(\frac{1}{12}\) =\(\frac{6}{12}\) =\(\frac{1}{2}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Problem Solving
Use the picture for 17-18

Question 17.
Sara is making a key chain using the bead design shown. What fraction of the beads in her design are either blue or red?
Answer:
Explanation:
Let us consider dark black as red
and light black as blue
Number of beads are 15
Number of red beads are \(\frac{5}{15}\)
Number of black beads are \(\frac{6}{15}\)
Question 18.
H.O.T. Multi-Step In making the key chain, Sara uses the pattern of beads 3 times. After the key chain is complete, what fraction of the beads in the key chain are either white or blue?

Answer:
Question 19.
Write Math Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. He claims to have \(\frac{3}{10}\) of the original spool of twine leftover. How you know whether Jamie’s claim is reasonable.
Answer: Yes. Jamie’s claim is reasonable.
Explanation:
Jamie had \(\frac{4}{5}\) of a spool of twine. He then used \(\frac{1}{2}\) of a spool of twine to make friendship knots. So \(\frac{3}{10}\) of the original spool of twine leftover. Since
\(\frac{4}{5}\) –\(\frac{1}{2}\) = \(\frac{8}{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\)
He claims to have \(\frac{3}{10}\) of the original spool of twine leftover. So it is equla to what he leftover. So his claim is reasonabale.
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 20.
Apply Students are voting for a new school mascot. So far, the results show that \(\frac{3}{10}\) of the students voted for “Fightin’ Titan,” \(\frac{1}{2}\) of the students voted for “Nifty Knight,” and the rest of the students have not voted yet. What fraction of the student population has not voted yet?
(A) \(\frac{3}{10}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{4}{5}\)
Answer: (C) \(\frac{1}{5}\)
Explanation:
So far, the results show that \(\frac{3}{10}\) of the students voted for “Fightin’ Titan,” \(\frac{1}{2}\) of the students voted for “Nifty Knight,” Then \(\frac{8}{10}\) voted. Since
\(\frac{3}{10}\) +\(\frac{1}{2}\) = \(\frac{8}{10}\)
So \(\frac{1}{5}\) of the students have not voted yet. Since
1- \(\frac{8}{10}\) = \(\frac{1}{5}\)
Question 21.
Tina spent \(\frac{3}{5}\) of her paycheck on a trip to the beach. She spent \(\frac{3}{8}\) of her paycheck on new clothes for the trip. What fraction of her paycheck did Tina spend on the trip and clothes together?
(A) \(\frac{9}{40}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{7}{8}\)
(D) \(\frac{39}{40}\)
Answer: (D) \(\frac{39}{40}\)
Explanation:
Tina spent \(\frac{3}{5}\) of her paycheck on a trip to the beach. She spent \(\frac{3}{8}\) of her paycheck on new clothes for the trip. So Tortal Spent is \(\frac{39}{40}\)
\(\frac{3}{5}\) + \(\frac{3}{8}\) = \(\frac{39}{40}\)
Question 22.
Multi-Step On Friday, \(\frac{1}{6}\) of band practice was spent trying on uniforms. The band spent \(\frac{1}{4}\) of practice on marching. What fraction of practice time was left for playing music?
(A) \(\frac{5}{12}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{7}{12}\)
(D) \(\frac{1}{4}\)
Answer: (C) \(\frac{7}{12}\)
Explanation:
\(\frac{1}{6}\) of band practice was spent trying on uniforms. The band spent \(\frac{1}{4}\) of practice on marching. So Total time spent is \(\frac{5}{12}\). So Time left is \(\frac{7}{12}\)
\(\frac{1}{6}\) + \(\frac{1}{4}\) = \(\frac{5}{12}\)
1-\(\frac{5}{12}\) =\(\frac{7}{12}\)
Texas Test Prep
Question 23.
Which equation represents the fraction of beads that are green or yellow?
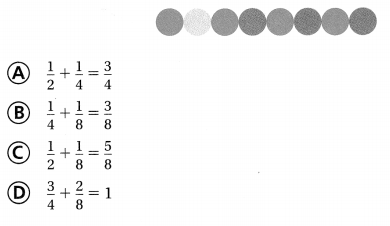
Answer:
Texas Go Math Grade 5 Lesson 5.5 Homework and Practice Answer Key
Find the sum or difference. Write your answer in simplest form.
Question 1.
\(\frac{1}{5}\) + \(\frac{1}{2}\) ____________
Answer:
\(\frac{1}{5}\) + \(\frac{1}{2}\) = \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 2.
\(\frac{2}{3}\) + \(\frac{1}{6}\) ____________
Answer:
\(\frac{2}{3}\) + \(\frac{1}{6}\) = \(\frac{4}{6}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 3.
\(\frac{1}{4}\) + \(\frac{2}{3}\) ____________
Answer:
\(\frac{1}{4}\) + \(\frac{2}{3}\) = \(\frac{3}{12}\) + \(\frac{8}{12}\) = \(\frac{11}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 4.
\(\frac{3}{4}\) + \(\frac{1}{8}\) ____________
Answer:
\(\frac{3}{4}\) + \(\frac{1}{8}\) = \(\frac{6}{8}\) + \(\frac{1}{8}\) = \(\frac{7}{8}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 5.
\(\frac{2}{9}\) + \(\frac{1}{3}\) ____________
Answer:
\(\frac{2}{9}\) + \(\frac{1}{3}\) = \(\frac{2}{9}\) + \(\frac{3}{9}\) = \(\frac{5}{9}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 6.
\(\frac{1}{2}\) + \(\frac{2}{6}\) ____________
Answer:
\(\frac{1}{2}\) + \(\frac{2}{6}\) = \(\frac{3}{6}\) + \(\frac{2}{6}\) = \(\frac{5}{6}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 7.
\(\frac{3}{10}\) + \(\frac{1}{3}\) ____________
Answer:
\(\frac{3}{10}\) + \(\frac{1}{3}\) = \(\frac{9}{30}\) + \(\frac{10}{30}\) = \(\frac{19}{30}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 8.
\(\frac{4}{18}\) + \(\frac{2}{6}\) ____________
Answer:
\(\frac{4}{18}\) + \(\frac{2}{6}\) = \(\frac{4}{18}\) + \(\frac{6}{18}\) = \(\frac{10}{18}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 9.
\(\frac{6}{12}\) – \(\frac{1}{3}\) ____________
Answer:
\(\frac{6}{12}\) – \(\frac{1}{3}\) = \(\frac{6}{12}\) – \(\frac{4}{12}\) = \(\frac{2}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 10.
\(\frac{3}{4}\) – \(\frac{1}{6}\) ____________
Answer:
\(\frac{3}{4}\) – \(\frac{1}{6}\) = \(\frac{9}{12}\) – \(\frac{2}{12}\) = \(\frac{7}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 11.
\(\frac{5}{7}\) – \(\frac{1}{2}\) ____________
Answer:
\(\frac{5}{7}\) – \(\frac{1}{2}\) = \(\frac{10}{14}\) – \(\frac{7}{14}\) = \(\frac{3}{14}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 12.
\(\frac{8}{9}\) – \(\frac{2}{3}\) ____________
Answer:
\(\frac{8}{9}\) – \(\frac{2}{3}\) = \(\frac{8}{9}\) – \(\frac{6}{9}\) = \(\frac{2}{9}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 13.
\(\frac{5}{9}\) – \(\frac{1}{6}\) ____________
Answer:
\(\frac{5}{9}\) – \(\frac{1}{6}\) = \(\frac{10}{18}\) – \(\frac{3}{18}\) = \(\frac{7}{18}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 14.
\(\frac{2}{3}\) – \(\frac{1}{4}\) ____________
Answer:
\(\frac{2}{3}\) – \(\frac{1}{4}\) = \(\frac{8}{12}\) – \(\frac{3}{12}\) = \(\frac{5}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 15.
\(\frac{7}{14}\) – \(\frac{2}{7}\) ____________
Answer:
\(\frac{7}{14}\) – \(\frac{2}{7}\) = \(\frac{7}{14}\) – \(\frac{4}{14}\) = \(\frac{3}{14}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 16.
\(\frac{5}{6}\) – \(\frac{3}{4}\) ____________
Answer:
\(\frac{5}{6}\) – \(\frac{3}{4}\) = \(\frac{10}{12}\) – \(\frac{9}{12}\) = \(\frac{1}{12}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Find the unknown number.
Question 17.
\(\frac{7}{12}\) – ☐ = \(\frac{1}{6}\)
☐ = _____________
Answer:
\(\frac{7}{12}\) – \(\frac{5}{12}\) = \(\frac{1}{6}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 18.
\(\frac{5}{18}\) + ☐ = \(\frac{1}{2}\)
☐ = _____________
Answer:
\(\frac{5}{18}\) + \(\frac{4}{18}\) = \(\frac{1}{2}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 19.
\(\frac{7}{10}\) – ☐ = \(\frac{2}{5}\)
☐ = ______________
Answer:
\(\frac{7}{10}\) – \(\frac{3}{10}\) = \(\frac{2}{5}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Question 20.
☐ + \(\frac{1}{9}\) = \(\frac{1}{3}\)
☐ = _______________
Answer:
\(\frac{2}{9}\) + \(\frac{1}{9}\) = \(\frac{1}{3}\)
Explanation:
Step 1: The least common denominator is found
Step 2: written equivalent fractions with equal denominators
Step 3: write the answer in simplest form.
Problem Solving
Question 21.
There are 12 students in the pep squad. Three students are wearing white shirts. Six students are wearing blue shirts. What fraction of the students in the pep squad are wearing either white or blue shirts?
Answer: \(\frac{1}{4}\) wearing the white shirts and \(\frac{1}{2}\) wearing the blue shirts.
Explanation:
There are 12 students in the pep squad. Three students are wearing white shirts.
\(\frac{3}{12}\) = \(\frac{1}{4}\)
Six students are wearing blue shirts.
\(\frac{6}{12}\) = \(\frac{1}{2}\)
Question 22.
Tiffany ran \(\frac{5}{6}\) mile. Shayne ran \(\frac{3}{4}\) mile. Who ran farther? How much farther?
Answer:
Lesson Check
Fill in the bubble completely to show your answer.
Question 23.
Mr. Benson spent \(\frac{2}{5}\) of the monthly budget on rent and \(\frac{3}{10}\) of the budget on food. What fraction of Mr. Benson’s budget was spent on rent and food?
(A) \(\frac{1}{3}\)
(B) \(\frac{3}{10}\)
(C) \(\frac{7}{10}\)
(D) \(\frac{1}{2}\)
Answer: (C) \(\frac{7}{10}\)
Explanation:
Mr. Benson spent \(\frac{2}{5}\) of the monthly budget on rent and \(\frac{3}{10}\) of the budget on food.
Sum of \(\frac{2}{5}\) and \(\frac{3}{10}\) is \(\frac{7}{10}\) .
Since
\(\frac{3}{10}\)+ \(\frac{2}{5}\)= \(\frac{7}{10}\) .
Question 24.
The Ortega family made \(\frac{15}{16}\) pound of confetti for the annual Fiesta celebration in San Antonio. They used \(\frac{1}{4}\) pound to make confetti filled eggs. How much confetti is left to use next year?
(A) \(\frac{11}{16}\) pound
(B) \(\frac{9}{16}\) pound
(C) \(\frac{4}{5}\) pound
(D) \(\frac{3}{4}\) pound
Answer: (A) \(\frac{11}{16}\) pound
Explanation:
The Ortega family made \(\frac{15}{16}\) pound of confetti for the annual Fiesta celebration in San Antonio. They used \(\frac{1}{4}\) pound to make confetti filled eggs. confetti is left to use next year is \(\frac{11}{16}\) pound. Since
\(\frac{15}{16}\) – \(\frac{1}{4}\) = \(\frac{11}{16}\) pound
Use the recipe for 25-26.

Question 25.
If Rory measures the lemon juice and the vanilla extract into one spoon before adding them to the blender, how much liquid will be in the spoon?
(A) \(\frac{5}{8}\) teaspoon
(B) \(\frac{1}{5}\) teaspoon
(C) \(\frac{1}{4}\) teaspoon
(D) \(\frac{3}{8}\) teaspoon
Answer: (A) \(\frac{5}{8}\) teaspoon
Explanation:
Sum of lemon juice and the vanilla extract is
\(\frac{1}{2}\) teaspoon + \(\frac{1}{8}\) teaspoon = \(\frac{5}{8}\) teaspoon
Question 26.
Multi-Step Rory has \(\frac{5}{8}\) cup of milk. How much milk does she have left after she doubles the recipe for the smoothie?
(A) \(\frac{3}{8}\) cup
(B) \(\frac{1}{8}\) cup
(C) \(\frac{3}{4}\) cup
(D) \(\frac{1}{2}\) cup
Answer: (B) \(\frac{1}{8}\) cup
Explanation:
she doubles the recipe for the smoothie. So it is \(\frac{1}{2}\) cup. Since
\(\frac{1}{4}\) cup + \(\frac{1}{4}\) cup = \(\frac{1}{2}\) cup.
Rory has \(\frac{5}{8}\) cup of milk. She left \(\frac{1}{8}\) cup of milk.
Since
\(\frac{5}{8}\) –\(\frac{1}{2}\) cup. = \(\frac{1}{8}\)
Question 27.
Multi-Step Torn has \(\frac{7}{8}\) cup of olive oil. He uses \(\frac{1}{2}\) cup to make salad dressing and \(\frac{1}{4}\) cup to make tomato sauce. How much olive oil does Torn have left?
(A) \(\frac{5}{4}\) cups
(B) \(\frac{5}{8}\) cup
(C) \(\frac{3}{8}\) cup
(D) \(\frac{1}{8}\) cup
Answer: (D) \(\frac{1}{8}\) cup
Explanation:
\(\frac{1}{2}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
and
\(\frac{7}{8}\) cup – \(\frac{3}{4}\) cup = \(\frac{1}{8}\) cup