Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 5.1 Answer Key Addition with Unequal Denominators.
Texas Go Math Grade 5 Lesson 5.1 Answer Key Addition with Unequal Denominators
Investigate
Hilary is using red fabric to make a tote bag. She uses one piece that is \(\frac{1}{2}\) yard long. She uses another piece that is \(\frac{1}{4}\) yard long. How much red fabric does she use?
Materials; fraction strips; MathBoard
A. Find \(\frac{1}{2}\) + \(\frac{1}{4}\). Place a \(\frac{1}{2}\) strip and a \(\frac{1}{4}\) strip under the 1-whole strip on your MathBoard.

Answer:

B. Find fraction strips, all with the same denominator, that are equivalent to \(\frac{1}{2}\) and \(\frac{1}{4}\) and fit exactly under the sum \(\frac{1}{2}\) + \(\frac{1}{4}\). Record the addends, using equal denominators.
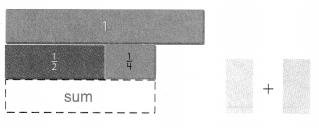
Answer: 3/4
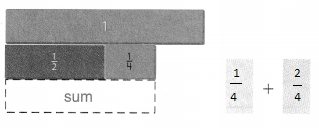
C. Record the sum in simplest form. \(\frac{1}{2}\) + \(\frac{1}{4}\) = ___________
So, Hilary uses ___________ yard of fabric.
Answer: So, Hilary uses \(\frac{3}{4}\) yard of fabric.
Record the sum in simplest form. \(\frac{1}{2}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
Math Talk
Mathematical Processes
How can you tell if the sum of the fractions is less than 1?
Answer:
Fractions greater than 1 have numerators larger than their denominators; those that are less than 1 have numerators smaller than their denominators; the rest are equal to 1.
Draw Conclusions
Question 1.
Describe how you would determine what fraction strips, all with the same denominator, would fit exactly under \(\frac{1}{2}\) + \(\frac{1}{3}\). What are they?
Answer:
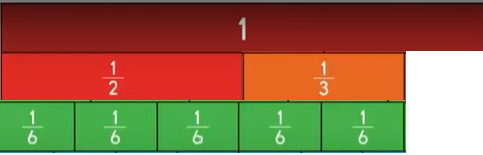
Explanation:
The denominator is 6
Which would fit exactly under \(\frac{1}{6}\) + \(\frac{1}{6}\)+ \(\frac{1}{6}\) + \(\frac{1}{6}\)+\(\frac{1}{6}\) + \(\frac{1}{6}\).
Question 2.
H.O.T. Explain the difference between finding fraction strips with the same denominator for \(\frac{1}{2}\) + \(\frac{1}{3}\) and \(\frac{1}{2}\) + \(\frac{1}{4}\).
Answer:
Make Connections
Sometimes, the sum of two fractions is greater than 1. When adding fractions with unequal denominators, you can use the 1-whole strip to help determine If a sum is greater than 1 or less than 1.
Use fraction strips to solve. \(\frac{3}{5}\) + \(\frac{1}{2}\)
STEP 1:
Work with another student. Place three \(\frac{1}{5}\) fraction strips under the 1-whole strip on your MathBoard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{5}\) strips.
STEP 2:
Find fraction strips, all with the same denominator, that are equivalent to \(\frac{3}{5}\) and \(\frac{1}{2}\). Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{3}{5}\) = __________ \(\frac{1}{2}\) = __________
STEP 3:
Add the fractions with equal denominators. Use the 1-whole strip to rename the sum in simplest form.
\(\frac{3}{5}\) + \(\frac{1}{2}\) = __________ + _________
= __________ or _________
Think: How many fraction strips with the same denominator are equal to 1 whole?
Answer:
step 1:

Explanation:
Placed three \(\frac{1}{5}\) fraction strips under the 1-whole strip on your MathBoard. Then place a \(\frac{1}{2}\) fraction strip beside the three \(\frac{1}{5}\) strips.
step 2:
Place the fraction strips under the sum. At the right, draw a picture of the model and write the equivalent fractions.
\(\frac{3}{5}\) = 6\(\frac{1}{10}\)
\(\frac{1}{2}\) = 5\(\frac{1}{10}\)
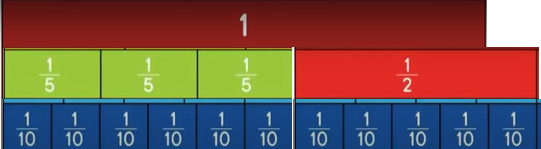
step 3:
\(\frac{3}{5}\) + \(\frac{1}{2}\) = 6\(\frac {1}{10}\) + 5\(\frac{1}{10}\)
= \(\frac{11}{10}\)

Math Talk
Mathematical Processes
In what step did you find out that the answer is greater than 1? Explain.
Answer: In step 2
Explanation:
\(\frac{3}{5}\) =6\(\frac{1}{10}\)
\(\frac{1}{2}\) =5\(\frac{1}{10}\)

Share and Show
Use fraction strips to find the sum. Write your answer in simplest form.
Question 1.
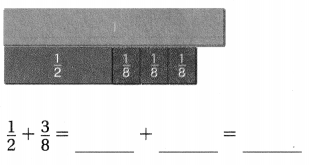
Answer:

Explanation:
Place the fraction strips with the same denominator 8, that are equivalent to \(\frac{1}{2}\)
then Added
Question 2.

Answer:
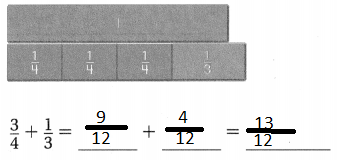
Explanation:
Place the fraction strips with the same denominator of 12, that are equivalent to \(\frac{3}{4}\) and \(\frac{1}{3}\). Then Added.
Use fraction strips to find the sum. Write your answer in simplest form.
Question 3.
\(\frac{2}{5}\) + \(\frac{3}{10}\) = __________
Answer: \(\frac{7}{10}\)
Explanation:
\(\frac{2}{5}\) + \(\frac{3}{10}\) = \(\frac{4}{10}\) + \(\frac{3}{10}\) = \(\frac{7}{10}\)
or
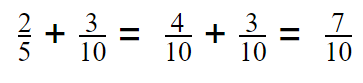
Question 4.
\(\frac{1}{4}\) + \(\frac{1}{12}\) = ___________
Answer: \(\frac{1}{3}\)
Explanation:
\(\frac{1}{4}\) + \(\frac{1}{12}\) = \(\frac{3}{12}\) + \(\frac{1}{12}\) = \(\frac{4}{12}\) = \(\frac{1}{3}\)
or

Question 5.
\(\frac{1}{2}\) + \(\frac{3}{10}\) = ____________
Answer: \(\frac{4}{5}\)
Explanation:
\(\frac{1}{2}\) + \(\frac{3}{10}\) = \(\frac{5}{10}\) + \(\frac{3}{10}\) = \(\frac{8}{10}\) = \(\frac{4}{5}\)
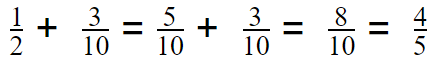
Problem Solving
Question 6.
H.O.T. Multi-Step Maya makes trail mix by combining \(\frac{1}{3}\) cup mixed nuts, \(\frac{1}{4}\) cup of dried fruit, and \(\frac{1}{6}\) cup of chocolate morsels. What is the total amount of ingredients in her trail mix?

Answer: \(\frac{3}{4}\)
Explanation:
\(\frac{1}{3}\) + \(\frac{1}{4}\) + \(\frac{1}{6}\)= \(\frac{4}{12}\) + \(\frac{3}{12}\) +\(\frac{2}{12}\) = \(\frac{9}{12}\) = \(\frac{3}{4}\)
Question 7.
H.O.T. Pose a Problem Write a new problem using different amounts for ingredients Maya used. Each amount should be a fraction with a denominator of 2, 3, or 4.
Answer:
Maya makes trail mix by combining \(\frac{1}{2}\) cup mixed nuts, \(\frac{1}{3}\) cup of dried fruit, and \(\frac{1}{4}\) cup of chocolate morsels. What is the total amount of ingredients in her trail mix?
Question 8.
Use Diagrams Solve the problem you wrote. Draw a picture of the fractions strips you use to solve your problem.
Answer: \(\frac{13}{12}\)
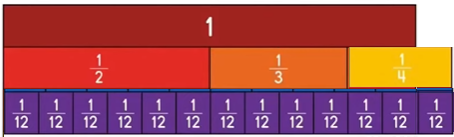
Question 9.
Explain why you chose the amounts you did for your problem.
Answer: in the question asked use different amounts for ingredients and Each amount should be a fraction with a denominator of 2, 3, or 4.
Question 10.
Write Math Explain how using fraction strips with equal denominators makes it possible to add fractions with unequal denominators.
Answer:
Think of the fruit analogy?
Does it make sense to add two bananas plus one watermelon? The units do not make sense for the sum.
BUT … we could think about changing both of them to common units, servings of fruit. If one banana serves one person and one watermelon serves ten people, then we could convert:
- two bananas + one watermelon =
- = two fruit servings + ten fruit servings =
- = twelve servings of fruit
Example:

Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 11.
In a garden, bluebonnets occupy \(\frac{7}{10}\) of the garden. After winter, the bluebonnets spread to cover another \(\frac{1}{5}\) of the garden. What fraction of the garden is now covered in bluebonnets?
(A) \(\frac{1}{5}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{8}{10}\)
(D) \(\frac{9}{10}\)
Answer: D
Explanation:
\(\frac{7}{10}\) + \(\frac{1}{5}\) = \(\frac{9}{10}\)
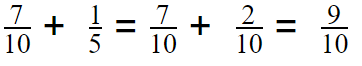
Question 12.
Ling is using fraction strips to add \(\frac{2}{3}\) and \(\frac{7}{12}\). The sum is one whole, plus how many twelfths?
(A) 1
(B) 2
(C) 3
(D) 4
Answer: C
Explanation:

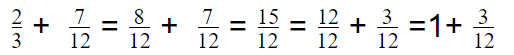
Question 13.
Multi-Step Juan uses \(\frac{1}{5}\) liter to water a small plant, and he uses \(\frac{1}{2}\) liter to water a large plant. Now he has \(\frac{2}{10}\) liter Left in the pitcher. How much water did Juan have in the beginning?
(A) \(\frac{3}{5}\) L
(B) \(\frac{9}{10}\) L
(C) \(\frac{1}{10}\) L
(D) \(\frac{3}{10}\) L
Answer: B
Explanation:
Juan uses \(\frac{1}{5}\) liter to water a small plant, and he uses \(\frac{1}{2}\) liter to water a large plant.
So total water he used \(\frac{7}{10}\) L.
Now he has \(\frac{2}{10}\) liter Left in the pitcher.
So Juan have water in the beginning is \(\frac{9}{10}\) L. Since
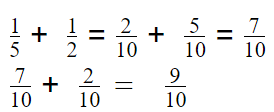
Texas Test Prep
Question 14.
Wilhelm is making a pie. He uses \(\frac{1}{2}\) cup of blueberries and \(\frac{2}{3}\) cup of raspberries. What is the total amount of berries in Wilhelm’s pie?
(A) \(\frac{3}{5}\) cup
(B) \(\frac{2}{6}\) cup
(C) \(\frac{7}{6}\) cups
(D) \(\frac{3}{6}\) cup
Answer: \(\frac{7}{6}\) cups
Explanation:
He uses \(\frac{1}{2}\) cup of blueberries and \(\frac{2}{3}\) cup of raspberries.
Sum of \(\frac{1}{2}\) + \(\frac{2}{3}\) = \(\frac{7}{6}\)

Texas Go Math Grade 5 Lesson 5.1 Homework and Practice Answer Key
Use fraction strips to find the sum. Write your answer in the simplest form.
Question 1.

Answer:
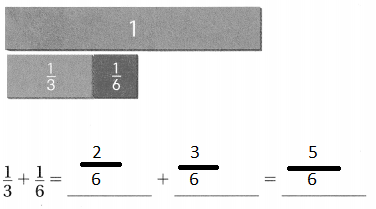
Explanation:
To add the given fractions, did the denominator equal first then added
Question 2.
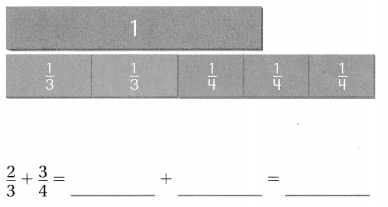
Answer:
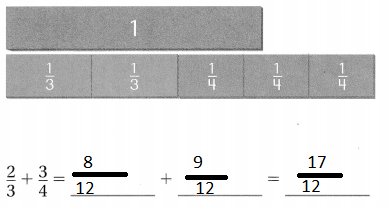
Explanation:
To add the given fractions, did the denominator equal first then added
Question 3.
\(\frac{1}{6}\) + \(\frac{3}{4}\) = ____________
Answer:\(\frac{11}{12}\)
Explanation:
To add the given fractions, did the denominator equal first then added
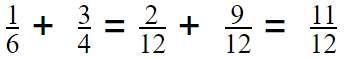
Question 4.
\(\frac{5}{6}\) + \(\frac{1}{2}\) = ____________
Answer: \(\frac{8}{6}\)
Explanation:
To add the given fractions, did the denominator equal first then added
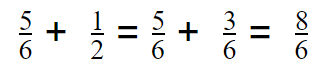
Question 5.
\(\frac{1}{2}\) + \(\frac{2}{5}\) = _____________
Answer: \(\frac{9}{10}\)
Explanation:
To add the given fractions, did the denominator equal first then added
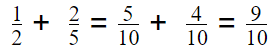
Question 6.
\(\frac{1}{4}\) + \(\frac{2}{3}\) = ______________
Answer: \(\frac{11}{12}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{1}{4}\) + \(\frac{2}{3}\) = \(\frac{3}{12}\) + \(\frac{8}{12}\) = \(\frac{11}{12}\)
Question 7.
\(\frac{1}{3}\) + \(\frac{5}{6}\) = _____________
Answer: \(\frac{7}{6}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{1}{3}\) + \(\frac{5}{6}\) = \(\frac{2}{6}\) + \(\frac{5}{6}\) = \(\frac{7}{6}\)
Question 8.
\(\frac{3}{5}\) + \(\frac{3}{10}\) = ______________
Answer: \(\frac{9}{10}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{3}{5}\) + \(\frac{3}{10}\) = \(\frac{6}{10}\) + \(\frac{3}{10}\) = \(\frac{9}{10}\)
Question 9.
\(\frac{1}{8}\) + \(\frac{3}{4}\) = _____________
Answer: \(\frac{7}{8}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{1}{8}\) + \(\frac{3}{4}\) = \(\frac{1}{8}\) + \(\frac{6}{8}\) = \(\frac{7}{8}\)
Question 10.
\(\frac{7}{10}\) + \(\frac{1}{2}\) = _____________
Answer: \(\frac{7}{8}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{7}{10}\) + \(\frac{1}{2}\) = \(\frac{7}{10}\) + \(\frac{5}{10}\) = \(\frac{12}{10}\) = \(\frac{6}{5}\)
Question 11.
\(\frac{5}{6}\) + \(\frac{1}{12}\) = _____________
Answer: \(\frac{11}{12}\)
Explanation:
To add the given fractions, did the denominator equal first then added
\(\frac{5}{6}\) + \(\frac{1}{12}\) = \(\frac{10}{12}\) + \(\frac{1}{12}\) = \(\frac{11}{12}\)
Problem Solving
Question 12.
Cooper is grating cheese for the family taco dinner. He grates \(\frac{1}{2}\) cup of cheddar cheese and \(\frac{3}{4}\) cup of monterey jack cheese. How much cheese does Cooper grate?
Answer: Cooper grate \(\frac{5}{4}\) cup of cheese
Explanation:
Cooper grates \(\frac{1}{2}\) cup of cheddar cheese and \(\frac{3}{4}\) cup of monterey jack cheese. then total cheese is sum of \(\frac{1}{2}\) cup of cheddar cheese and \(\frac{3}{4}\) cup of monterey jack cheese. So Total cheese is \(\frac{5}{4}\)
\(\frac{1}{2}\)+\(\frac{3}{4}\) =\(\frac{2}{4}\)+\(\frac{3}{4}\) = \(\frac{5}{4}\)
Question 13.
Jasmine has to mix \(\frac{3}{4}\) cup of flour and \(\frac{3}{8}\) cup of cornmeal. She has a container that holds 1 cup. Can Jasmine mix the flour and cornmeal in the container? Explain.
Answer: Jasmine Can not mix the flour and cornmeal in the container. Since total mix of flour and cornmeal is 1/8 cup more than cup.
Explanation:
Jasmine has to mix \(\frac{3}{4}\) cup of flour and \(\frac{3}{8}\) cup of cornmeal. So Sum of flour and cornmeal is \(\frac{9}{8}\)
if divide in to fraction strips of same denominator the \(\frac{8}{8}\) + \(\frac{1}{8}\). \(\frac{8}{8}\) is equals to 1 cup. So she can not mix in the container.
Lesson Check
Fill in the bubble completely to show your answer.
Question 14.
Julio spent \(\frac{1}{10}\) of his weekly allowance on a set of markers and \(\frac{2}{5}\) of it on a book. What fraction of Julio’s allowance is this altogether?
(A) \(\frac{1}{2}\)
(B) \(\frac{3}{10}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{1}{5}\)
Answer: \(\frac{1}{2}\)
Explanation:
\(\frac{1}{10}\) + \(\frac{2}{5}\) = \(\frac{1}{10}\) + \(\frac{4}{10}\) =\(\frac{5}{10}\) = \(\frac{1}{2}\)
Question 15.
Kate is using fraction strips to add \(\frac{4}{10}\) and \(\frac{4}{5}\). She uses one whole strip to represent the sum. How many fifths strips does she need to complete the sum?
(A) 1
(B) 2
(C) 5
(D) 8
Answer: A
Explanation:

one extra strip is needed to complete the sum
Question 16.
Which fraction correctly completes the equation?
\(\frac{6}{8}\) + \(\frac{}{}\) = 1
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{3}{8}\)
(D) \(\frac{1}{4}\)
Answer: D
Explanation:
\(\frac{6}{8}\) + \(\frac{1}{4}\) = \(\frac{6}{8}\) + \(\frac{2}{8}\) = \(\frac{8}{8}\) = 1
Question 17.
An apple was cut into 8 equal-size pieces. Stacy ate \(\frac{1}{4}\) of the apple. Tony ate \(\frac{3}{8}\) of the apple. What part of the apple did Stacy and Tony eat in all?
(A) \(\frac{1}{2}\)
(B) \(\frac{5}{8}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{1}{4}\)
Answer: B
Explanation:
Equal the all denominators:
Stacy ate \(\frac{1}{4}\) of the apple = \(\frac{1}{4}\) = \(\frac{2}{8}\)
Tony ate \(\frac{3}{8}\) of the apple = \(\frac{3}{8}\)
Stacy and Tony ate = \(\frac{3}{8}\) + \(\frac{2}{8}\)= \(\frac{5}{8}\)
Question 18.
Multi-Step Last weekend, Beatrice walked her poodle \(\frac{2}{3}\) mile on Saturday and \(\frac{5}{6}\) mile on Sunday. Fiona walked her beagle \(\frac{1}{3}\) mile on Saturday and \(\frac{1}{2}\) mile on Sunday. How much farther did the poodle walk last weekend than the beagle?
(A) \(\frac{1}{2}\) mile
(B) 1\(\frac{1}{3}\) miles
(C) \(\frac{2}{3}\) mile
(D) 1\(\frac{1}{2}\) miles
Answer: C
Explanation:
Last weekend, Beatrice walked her poodle \(\frac{2}{3}\) mile on Saturday
and \(\frac{5}{6}\) mile on Sunday.
Fiona walked her beagle \(\frac{1}{3}\) mile on Saturday
and \(\frac{1}{2}\) mile on Sunday.
\(\frac{2}{3}\) + \(\frac{5}{6}\) = \(\frac{4}{6}\) + \(\frac{5}{6}\) = \(\frac{9}{6}\) = \(\frac{3}{2}\)
\(\frac{1}{3}\) + \(\frac{1}{2}\) = \(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
\(\frac{3}{2}\) – \(\frac{5}{6}\) = \(\frac{9}{6}\) – \(\frac{5}{6}\) = \(\frac{2}{3}\)
Question 19.
Multi-Step Rick worked in his garden on Friday. He pulled weeds for \(\frac{5}{6}\) hour, planted seeds for \(\frac{1}{2}\) hour, and watered for \(\frac{1}{6}\) hour. How much time did Rick spend working in his garden on Friday?
(A) \(\frac{1}{2}\) hour
(B) 1 hour
(C) 1\(\frac{1}{3}\) hours
(D) 1\(\frac{1}{2}\) hours
Answer: D
Explanation:
\(\frac{5}{6}\) +\(\frac{1}{2}\) + \(\frac{1}{6}\) = \(\frac{5}{6}\) +\(\frac{3}{6}\) +\(\frac{1}{6}\) = \(\frac{9}{6}\) = \(\frac{6}{6}\) +\(\frac{3}{6}\) = 1 + \(\frac{1}{2}\)