Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 5.7 Answer Key Use Properties of Addition.
Texas Go Math Grade 4 Lesson 5.7 Answer Key Use Properties of Addition
Essential Question
How can properties help you add fractions with like denominators?
Answer:
the commutative property of addition states that when finding a sum, changing the order of the addends will not change their sum. In symbols, the commutative property of addition says that for numbers
The associative property of addition states that when finding a sum, changing the way addends are grouped will not change their sum. In symbols, the associative property of addition says that for numbers
Unlock the Problem
Jane and her teammates are training for their track meet. On the first day of practice, they run 2\(\frac{4}{8}\) miles around the track. On the second day, they run 2\(\frac{1}{8}\) miles. On the last day of practice before the meet, they run \(\frac{7}{8}\) mile. How many miles did Jane and her teammates run to train for their track meet?
Use the Associative Property.
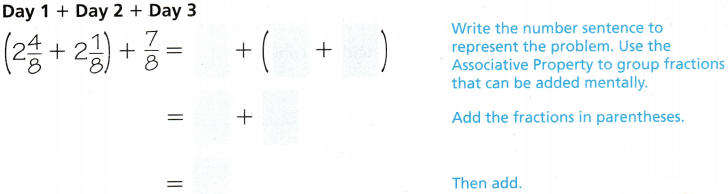
So, Jane and her teammates ran __________ miles to prepare for their track meet.
Answer:

Explanation:
So, Jane and her teammates ran \(\frac{44}{8}\) miles to prepare for their track meet.
Math Talk
Mathematical Processes
Explain why grouping the fractions differently makes it to find the sum.
Answer:
Because mixed fractions are again converted to fractions
to find the sum
Explain why you would not group 2\(\frac{4}{8}\) and \(\frac{7}{8}\) together in parentheses.
Answer:
One is fraction and the other is mixed fraction
Example Add. (2\(\frac{7}{8}\) + 2\(\frac{5}{8}\)) + 3\(\frac{3}{8}\)
Use the Associative Property
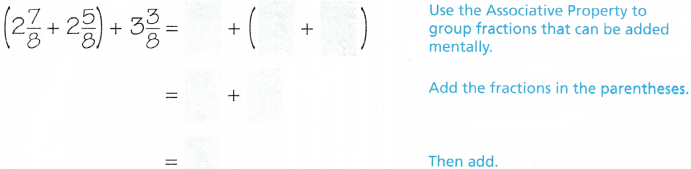
Answer:

Explanation:
By using the associative property solved the addition sum of mixed fraction.
Try This!
Subtraction is not commutative or associative. When you subtract, perform operations in parentheses first. Then subtract from left to right.
a. 5\(\frac{8}{12}\) – \(\frac{2}{12}\) – \(\frac{1}{12}\) = _______ – \(\frac{1}{12}\) = ____________
Answer:
5\(\frac{8}{12}\) – \(\frac{2}{12}\) – \(\frac{1}{12}\) = 5\(\frac{6}{12}\) – \(\frac{1}{12}\) = 5\(\frac{5}{12}\)
Explanation:
First subtracted the whole then subtracted the fractions
b. \(\left(5 \frac{8}{12}-\frac{2}{12}\right)-\frac{1}{12}\) = ____________ – \(\frac{1}{12}\) = ____________
Answer:
(5\(\frac{8}{12}\) – \(\frac{2}{12}\) )- \(\frac{1}{12}\) =(5\(\frac{6}{12}\))
(5\(\frac{6}{12}\)) – \(\frac{1}{12}\) = 5\(\frac{5}{12}\)
Explanation:
First subtracted the whole then subtracted the fractions
c. \(5 \frac{8}{12}-\left(\frac{2}{12}-\frac{1}{12}\right)\) = 5\(\frac{8}{12}\) – ____________ = ____________
Answer:
5\(\frac{8}{12}\) – (\(\frac{2}{12}\) – \(\frac{1}{12}\) )= 5\(\frac{1}{12}\)
5\(\frac{8}{12}\)– \(\frac{1}{12}\) = 5\(\frac{7}{12}\)
Explain how you can use your answers to parts b and c to conclude that subtraction is not associative.
Answer:
The answer are different from part b to part c.
Share and Show
Use the properties and mental math to solve. Write your answer in simplest form.
Question 1.
\(\left(2 \frac{5}{8}+\frac{1}{8}\right)+\frac{7}{8}\)
Answer:
\(\frac{21}{8}\) + 1
= \(\frac{29}{8}\)
Explanation:
Used mental math’s to solve the equation into simplest form
Question 2.
\(\frac{7}{12}+\left(\frac{5}{12}+\frac{2}{12}\right)\)
Answer:
\(\frac{14}{12}\) = 2\(\frac{2}{12}\)
Explanation:
Used mental math’s to solve the equation into simplest form
Question 3.
\(3 \frac{1}{4}+\left(2 \frac{3}{4}+6 \frac{2}{4}\right)\)
Answer:
\(\frac{18}{4}\) = 4\(\frac{2}{4}\)
Explanation:
Used mental math’s to solve the equation into simplest form
Problem Solving
Use the map to solve 4-5.
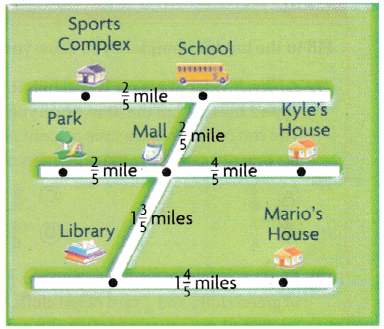
Question 4.
Multi-Step In the morning, Julie rides her hike from the sports complex to the school. In the afternoon, she rides from the school to the mall, and then to Kyle’s house. How far does Julie ride her bike?
Answer:
\(\frac{2}{5}\) + \(\frac{2}{5}\) +\(\frac{4}{5}\)
\(\frac{8}{5}\) mile far that Julie ride her bike.
Question 5.
H.O.T. On one afternoon, Mario walks from his house to the library. That evening, Mario walks from the library to the mall, and then to Kyle’s house. Describe how you can use the properties to find how far Mario walks.
Answer: By using the commutative property
Explanation:
(1\(\frac{4}{5}\) + 1\(\frac{3}{5}\) )+ \(\frac{4}{5}\)
2\(\frac{11}{5}\) = 4\(\frac{1}{5}\)
4\(\frac{1}{5}\) mile far Mario walks.
Question 6.
H.O.T. Analyze Explain how you would use the Associative Property to help you solve this problem. \(\left(6 \frac{2}{8}+5 \frac{3}{8}\right)+1 \frac{5}{8}\)
Answer:
6\(\frac{2}{8}\)+(5\(\frac{3}{8}\)+1\(\frac{5}{8}\))
Add the wholes 6+5+1=12
Add the fractions \(\frac{2}{8}\)+\(\frac{3}{8}\)+\(\frac{5}{8}\)
=\(\frac{10}{8}\)
=1\(\frac{2}{8}\) = 13\(\frac{2}{8}\)
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 7.
A bicycle rider trains on Type 3 hills for \(\frac{3}{8}\) of his practice time, Type 2 hills for \(\frac{1}{8}\) of the time, and Type HC hills for \(\frac{3}{8}\) of the time. The rest of the practice time is spent on flat ground. What part of his practice time does the rider train on hills?
Answer:
\(\frac{3}{8}\)+\(\frac{1}{8}\)+\(\frac{3}{8}\)
=\(\frac{7}{8}\)part of his practice time that the rider train on hills
Explanation:
Added the whole then added the fractions.
Question 8.
Marie is making a costume. She uses \(\frac{2}{4}\) yard of blue cloth, \(\frac{1}{4}\) yard of green cloth, and yard of red cloth. Which shows a way Marie could find the amount of cloth she uses?
(A) \(\frac{2}{4}+\left(\frac{1}{4}+\frac{1}{4}\right)\)
(B) \(\frac{2}{4}+\left(\frac{2}{4}+\frac{1}{4}\right)\)
(C) \(\frac{3}{4}+\left(\frac{1}{4}+\frac{1}{4}\right)\)
(D) \(\frac{1}{4}+\left(\frac{1}{4}+\frac{1}{4}\right)\)
Answer: A
Explanation:
\(\frac{2}{4}+\left(\frac{1}{4}+\frac{1}{4}\right)\) shows a way Marie that the amount of cloth she uses.
Question 9.
Multi-Step Otis needs 1 pound of apples to make an apple pie. He has \(\frac{3}{12}\) pound of yellow apples, \(\frac{4}{12}\) pound of red apples, and \(\frac{3}{12}\) pound of green apples. How many more pounds of apples does he need?
(A) \(\frac{6}{12}\) pound
(B) \(\frac{7}{12}\) pound
(C) \(\frac{10}{12}\) pound
(D) \(\frac{2}{12}\) pound
Answer: D
Explanation:
\(\frac{3}{12}\)+\(\frac{4}{12}\)+\(\frac{3}{12}\) = \(\frac{10}{12}\)
1- \(\frac{10}{12}\) = \(\frac{2}{12}\) pound of more apples he need
TEXAS Test Prep
Question 10.
Bill got an answer of \(\frac{8}{10}\) to the problem \(\left(\frac{9}{10}-\frac{4}{10}\right)-\frac{3}{10}\) Which statement shows the error he made?
(A) He did not subtract all the numbers.
(B) He subtracted \(\left(\frac{9}{10}-\frac{4}{10}\right)\) first.
(C) He regrouped as \(\frac{9}{10}-\left(\frac{4}{10}-\frac{3}{10}\right)\)
(D) He subtracted from left to right.
Answer: C
Explanation:
He regrouped as \(\frac{9}{10}-\left(\frac{4}{10}-\frac{3}{10}\right)\) this the error he made
Texas Go Math Grade 4 Lesson 5.7 Homework and Practice Answer Key
Use the properties and mental math to solve.
Write your answer in simplest form.
Question 1.
\(\frac{1}{5}+\left(\frac{4}{5}+\frac{2}{5}\right)\)
Answer:
\(\frac{1}{5}\) + \(\frac{6}{5}\)
= \(\frac{7}{5}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Question 2.
\(\left(\frac{3}{9}+\frac{5}{9}\right)+\frac{4}{9}\)
Answer:
\(\frac{8}{9}\) + \(\frac{4}{9}\)
= \(\frac{12}{9}\)
=1\(\frac{3}{9}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Question 3.
\(\left(\frac{2}{3}+\frac{2}{3}\right)+\frac{1}{3}\)
Answer:
\(\frac{4}{3}\) + \(\frac{1}{3}\)
= \(\frac{5}{3}\)
=1\(\frac{5}{3}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Question 4.
\(4 \frac{2}{6}+\left(2 \frac{4}{6}+3 \frac{3}{6}\right)\)
Answer:
4\(\frac{2}{6}\) +5 \(\frac{7}{6}\)
= 9\(\frac{9}{6}\) =10\(\frac{3}{6}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Question 5.
\(\left(2 \frac{3}{4}+1 \frac{3}{4}\right)+3 \frac{1}{4}\)
Answer:
3\(\frac{6}{4}\) + 3\(\frac{1}{4}\)
=6 \(\frac{7}{4}\)
=7\(\frac{3}{4}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Question 6.
\(1 \frac{2}{7}+\left(3 \frac{5}{7}+3 \frac{4}{7}\right)\)
Answer:
1\(\frac{2}{7}\) + 6\(\frac{9}{7}\)
= 7\(\frac{11}{7}\)
=8\(\frac{4}{7}\)
Explanation:
Used mental math’s to solve the equation into simplest form by using the properties
Problem Solving
Use the map for 7-8.
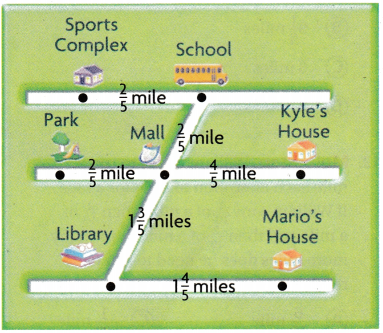
Question 7.
On Saturday, Mario walked from his house to the library. Later that day, he walked from the library to the mall, and then to the park. How far did Mario walk on Saturday?
Answer:
1\(\frac{4}{5}\)+1\(\frac{3}{5}\)+\(\frac{2}{5}\)
Explanation:
Add the whole 1+1=2
Added the fractions \(\frac{4+3+2}{5}\)
\(\frac{8}{5}\) = 3\(\frac{3}{5}\)
Question 8.
Kyle rode his bike from the library to the mall. Later he rode from the mall to school, and then to the sports complex. How far did Kyle ride his bike?
Answer:
1\(\frac{3}{5}\)+\(\frac{2}{5}\)+\(\frac{2}{5}\)
Explanation:
Add the whole 1=1
Added the fractions \(\frac{2+3+2}{5}\)
\(\frac{7}{5}\) = 2\(\frac{2}{5}\)
Lesson Check
Fill in the bubble completely to show your answer.
Question 9.
Robin is studying for a history test. She studies for \(\frac{3}{4}\) hour on both Friday and Saturday and 1\(\frac{1}{4}\) hour on Sunday. Robin writes \(\left(\frac{3}{4}+\frac{3}{4}\right)+1 \frac{1}{4}\) to find the amount of time she studied. Which shows another way Robin could find the amount of time she studied?
(A) \(\frac{3}{4}+\left(\frac{3}{4}+\frac{3}{4}\right)\)
(B) \(\frac{3}{4}+\left(\frac{3}{4}+\frac{1}{4}\right)\)
(C) \(\frac{3}{4}+\left(1 \frac{1}{4}+1 \frac{1}{4}\right)\)
(D) \(\frac{3}{4}+\left(\frac{3}{4}+1 \frac{1}{4}\right)\)
Answer: D
Explanation:
\(\frac{3}{4}+\left(\frac{3}{4}+1 \frac{1}{4}\right)\)is the another way that Robin could find the amount of time she studied.
Question 10.
At Hill School, the fourth grade classes each had a pizza party. Mr Dean’s class ate 5\(\frac{3}{8}\) Mrs. Sander’s class ate 4\(\frac{5}{8}\) pizzas, and Mrs. Carter’s class ate 5\(\frac{5}{8}\) pizzas. What is the total amount of pizza eaten by all three classes?
(A) 14\(\frac{7}{8}\) pizzas
(B) 14\(\frac{1}{2}\) pizzas
(C) 15\(\frac{5}{8}\) pizzas
(D) 15 pizzas
Answer: C
Explanation:
5\(\frac{3}{8}\) + 4\(\frac{5}{8}\) + 5\(\frac{5}{8}\)
Add the whole 5 +4+5= 14
Add the fractions \(\frac{13}{8}\)
15\(\frac{5}{8}\)
Question 11.
The distance from Jill’s house to the grocery store is 3\(\frac{7}{10}\) miles. The distance from the grocery store to the hank is \(\frac{2}{10}\) mile. The distance from the bank to the gym is 5\(\frac{1}{10}\) miles. If Jill drives from her house to the bank and then to the gym, how far has she traveled?
(A) 9 miles
(B) 9\(\frac{1}{5}\) miles
(C) 8 miles
(D) 8\(\frac{1}{5}\) miles
Answer: A
Explanation:
3\(\frac{7}{10}\)+\(\frac{2}{10}\)+5\(\frac{1}{10}\)
Add the whole 3+5=8
Add the fractions \(\frac{7+2+1}{10}\) = 1
8+1=9
Question 12.
At lunchtime, Dale’s Diner served a total of 2\(\frac{2}{6}\) pots of vegetable soup, 3\(\frac{5}{6}\) pots of chicken soup, and 4\(\frac{3}{6}\) pots of tomato soup. I low many pots of soup were served in all?
(A) 9\(\frac{2}{3}\) pots
(B) 10\(\frac{2}{3}\) pots
(C) 10\(\frac{1}{3}\) pots
(D) 9\(\frac{1}{3}\) pots
Answer: B
Explanation:
2\(\frac{2}{6}\) + 3\(\frac{5}{6}\)+4\(\frac{3}{6}\)
Add the whole 2+3+4= 9
Add the fractions \(\frac{2+5+3}{6}\) = \(\frac{10}{6}\)
= 10\(\frac{4}{6}\)
Question 13.
Multi-Step William wants to run a mile each afternoon to train for a race. If William runs \(\frac{3}{10}\) of a mile, then \(\frac{4}{10}\) of a mile and then \(\frac{2}{10}\) of a mile, how many more miles does he need to run to reach his goal?
(A) \(\frac{6}{10}\) mile
(B) \(\frac{9}{10}\) mile
(C) \(\frac{1}{10}\) mile
(D) \(\frac{7}{10}\) mile
Answer: C
Explanation:
\(\frac{3}{10}\) + \(\frac{4}{10}\) + \(\frac{2}{10}\)
Add the fractions directly \(\frac{3+4+2}{10}\)
1-\(\frac{9}{10}\) = \(\frac{1}{10}\)
Question 14.
Grace has 2\(\frac{1}{3}\) yards of red fabric, 2\(\frac{2}{3}\) yards of blue fabric, and 1\(\frac{2}{3}\) yards of green fabric. How much fabric does Grace have?
(A) 6\(\frac{2}{3}\) yards
(B) 5\(\frac{2}{3}\) yards
(C) 7\(\frac{2}{3}\) yards
(D) 3\(\frac{1}{3}\) yards
Answer: A
Explanation:
2\(\frac{1}{3}\) + 2\(\frac{2}{3}\) + 1\(\frac{2}{3}\)
Add the wholes 2+2+1 = 5
Add the fractions \(\frac{1+2+2}{3}\)
6\(\frac{2}{3}\) yards