Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 3.1 Answer Key Equivalent Fractions.
Texas Go Math Grade 4 Lesson 3.1 Answer Key Equivalent Fractions
Investigate
Materials
- color pencils
Joe cut a pan of brownies into third-size pieces. He kept and gave the rest away. Joe will not eat his part all at once. How can he cut his part into smaller, equal-size pieces?
A. Draw on the model to show how Joe could cut his part of the brownies into 2 equal pieces.
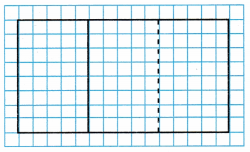
Answer:
You can rename these 2 equal pieces as a fraction of the original pan of brownies.
Suppose Joe had cut the original pan of brownies into equal pieces of this size.
How many pieces would there be? __________
Answer:
6
Explanation:
There are a total of 6 pieces that would be there.
What fraction of the pan is 1 piece? __________
Answer:
\(\frac{1}{6}\)
Explanation:
The fraction \(\frac{1}{6}\) of the pan is 1 piece.
What fraction of the pan is 2 pieces? __________
Answer:
\(\frac{2}{6}\)
Explanation:
The \(\frac{2}{6}\) of the pan is 2 pieces.
You can rename \(\frac{1}{3}\) as __________.
Answer:
\(\frac{2}{6}\)
Explanation:
You can rename \(\frac{1}{3}\) as \(\frac{2}{6}\).
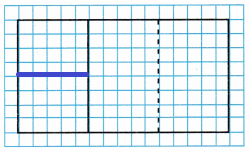
B. Now draw on the model to show how Joe could cut his part of the brownies into 4 equal pieces.
Answer:
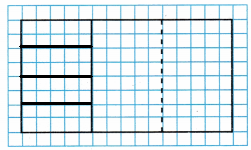
You can rename these 4 equal pieces as a fraction of the original pan of brownies.
Suppose Joe had cut the original pan of brownies into equal pieces of this size.
How many pieces would there be? __________
Answer:
12
Explanation:
There are 12 pieces that would be there.
What fraction of the pan is 1 piece? __________
Answer:
\(\frac{2}{6}\)
Explanation:
The fraction \(\frac{2}{6}\) of the pan is 1 piece.
What fraction of the pan is 4 pieces? __________
Answer:
\(\frac{4}{12}\)
Explanation:
You can rename \(\frac{1}{3}\) as __________ .
Answer:
You can rename \(\frac{1}{3}\) as \(\frac{4}{12}\)
C. Fractions that name the same amount are equivalent fractions. Write the equivalent fractions.
\(\frac{1}{3}\) = __________ = __________
Answer:
\(\frac{2}{6}\) = \(\frac{4}{12}\)
Make Connections
Savannah has \(\frac{2}{4}\) yard of ribbon, and Lin has \(\frac{3}{8}\) yard of ribbon. How can you determine whether Savannah and Lin have the same length of ribbon?
The equal sign (=) and not equal to sign (≠) show whether fractions are equivalent.
Tell whether \(\frac{2}{4}\) and \(\frac{3}{8}\) are equivalent. Write = or ≠.
STEP 1 Shade the amount of ribbon Savannah has.
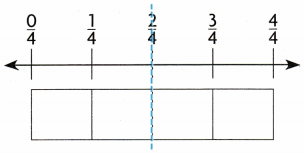
Answer:
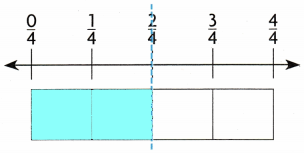
STEP 2 Shade the amount of ribbon Lin has.
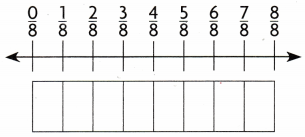
Think: \(\frac{2}{4}\) yard is not the same amount as \(\frac{3}{8}\) yard.
So, \(\frac{2}{4}\) _______ \(\frac{3}{8}\).
Answer:
\(\frac{2}{4}\) is not equal to \(\frac{3}{8}\)
Explanation:
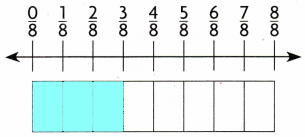
Math Talk
Mathematical Processes
How could you use a model to show that \(\frac{4}{8}\) = \(\frac{1}{2}\)?
Answer:
We could use a model by using fraction strips. Next, we need to line up 4 eighth-size parts below 1 half-size part.
Share and Show
Use the model to write an equivalent fraction.
Question 1.
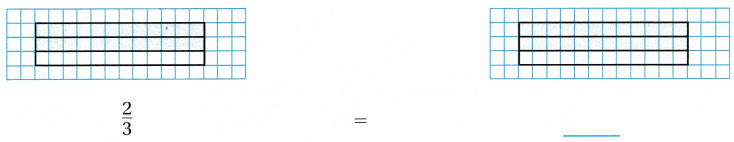
Answer:
The model to write an equivalent fraction is \(\frac{6}{9}\)
Explanation:
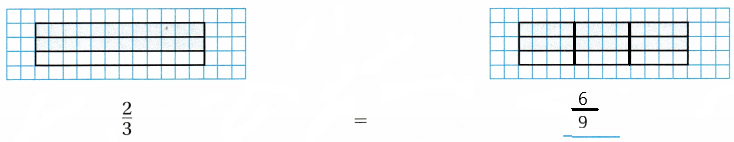
Tell whether the fractions are equivalent. Write = or
Question 2.
\(\frac{5}{8}\) ____________ \(\frac{2}{4}\)
Answer:
\(\frac{5}{8}\) is not equal to \(\frac{2}{4}\)
Explanation:
≠
Question 3.
\(\frac{5}{6}\) ____________ \(\frac{10}{12}\)
Answer:
Question 4.
\(\frac{1}{2}\) ____________ \(\frac{5}{10}\)
Answer:
Question 5.
H.O.T. Apply Does \(\frac{1}{3}\) = \(\frac{3}{9}\)? Explain
Answer:
Problem Solving
H.O.T. What’s the Error?
Question 6.
Reasoning Ben brought two pizzas to a party. He says that since \(\frac{1}{4}\) of each pizza is left, the same amount of each pizza is left. What is his error?

Describe Ben’s error
Answer:

Draw models of 2 pizzas with a different number of equal pieces. Use shading to show \(\frac{1}{4}\) of each pizza.
Answer:
Question 7.
H.O.T. Tia had \(\frac{3}{4}\) of her homework done. Maxwell had \(\frac{7}{12}\) of his homework done. Had they done the same amount of homework? Explain.
Answer:
Question 8.
Multi-Step Liu ran \(\frac{2}{3}\) of a mile, Toby ran \(\frac{3}{4}\) of a mile, and Raul ran \(\frac{8}{12}\) of a mile. Who of the three ran the same distance?
Answer:
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 9.
Students in Beth’s class made a sidewalk drawing on \(\frac{1}{6}\) of a sidewalk. Jim’s class made a drawing on an equivalent amount of another sidewalk. What fraction could be the amount of sidewalk Jim’s class drew on?
(A) \(\frac{1}{12}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{2}{12}\)
Answer:
\(\frac{2}{12}\)
Explanation:
The amount of sidewalk Jim’s class drew on is \(\frac{2}{12}\).
Question 10.
Use Diagrams The dough recipe used \(\frac{2}{5}\) cup of flour. Use the model. Which fraction is equivalent to \(\frac{2}{5}\)?
(A) \(\frac{1}{12}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{2}{12}\)
Answer:
Question 11.
Jon ate of a veggie pizza. Laura ate an equivalent amount of a cheese pizza. Which fraction could be the amount of cheese pizza that Laura ate?
(A) \(\frac{1}{4}\)
(B) \(\frac{2}{4}\)
(C) \(\frac{1}{8}\)
(D) \(\frac{2}{12}\)
Answer:
TEXAS Test Prep
Question 12.
Which fraction is equivalent to \(\frac{3}{5}\)?
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{1}{4}\)
Answer:
Texas Go Math Grade 4 Lesson 3.1 Homework and Practice Answer Key
Equivalent Fractions
Use the model to write an equivalent fraction.
Question 1.
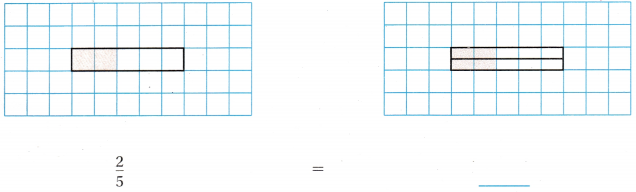
Answer:
Tell whether the fractions are equivalent. Write = or ≠.
Question 2.
\(\frac{3}{6}\) _______ \(\frac{1}{2}\)
Answer:
Question 3.
\(\frac{2}{3}\) _______ \(\frac{4}{5}\)
Answer:
Question 4.
\(\frac{1}{4}\) _______ \(\frac{4}{8}\)
Answer:
Question 5.
\(\frac{2}{5}\) _______ \(\frac{4}{10}\)
Answer:
Question 6.
\(\frac{1}{4}\) _______ \(\frac{1}{8}\)
Answer:
Question 7.
\(\frac{1}{6}\) _______ \(\frac{2}{12}\)
Answer:
Question 8.
\(\frac{2}{5}\) _______ \(\frac{6}{10}\)
Answer:
Question 9.
\(\frac{4}{12}\) _______ \(\frac{1}{3}\)
Answer:
Question 10.
\(\frac{1}{5}\) _______ \(\frac{2}{10}\)
Answer:
Question 11.
Sam ate \(\frac{1}{4}\) of a pizza. Claire ate \(\frac{2}{8}\) of a pizza. Did they eat the same amount of pizza? Explain.
Answer:
Question 12.
Lee spent \(\frac{1}{3}\) of his day doing chores. Carrie spent \(\frac{1}{6}\) of her day doing chores. Did Lee and Carrie spend the same amount of their day doing chores? Explain.
Answer:
\(\frac{1}{3}\) + \(\frac{1}{6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Explanation:
Lee and Carrie spend the same amount of their day doing chores is \(\frac{1}{2}\).
Lesson Check
Fill in the bubble completely to show your answer.
Question 13.
Which fraction is equivalent to \(\frac{6}{8}\)?
(A) \(\frac{8}{6}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{4}{6}\)
(D) \(\frac{6}{14}\)
Answer:
\(\frac{3}{4}\)
Explanation:
The fraction is equivalent to \(\frac{6}{8}\) is \(\frac{3}{4}\).
Question 14.
Which fraction is equivalent to \(\frac{2}{3}\)
(A) \(\frac{3}{5}\)
(B) \(\frac{3}{2}\)
(C) \(\frac{4}{5}\)
(D) \(\frac{6}{9}\)
Answer:
\(\frac{6}{9}\)
Explanation:
The fraction is equivalent to \(\frac{2}{3}\) is \(\frac{6}{9}\).
Question 15.
Which fraction is equivalent to the shaded area shown?
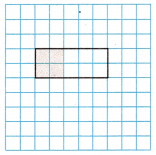
(A) \(\frac{5}{2}\)
(B) \(\frac{5}{5}\)
(C) \(\frac{2}{5}\)
(D) \(\frac{10}{4}\)
Answer:
\(\frac{2}{5}\)
Explanation:
The fraction is equivalent to the shaded area shown is \(\frac{2}{5}\).
Question 16.
Which fraction is equivalent to the shaded area shown?
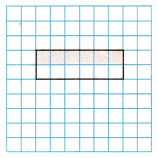
(A) \(\frac{6}{12}\)
(B) \(\frac{6}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{12}{3}\)
Answer:
\(\frac{6}{12}\)
Explanation:
The fraction is equivalent to the shaded area shown is \(\frac{6}{12}\).
Question 17.
Multi-Step Maria made one dozen cookies. She gave six of the cookies to her teacher and three of the cookies to her friend. ‘Which fraction is equivalent to the amount of cookies Maria gave away?
(A) \(\frac{3}{4}\)
(B) \(\frac{3}{6}\)
(C) \(\frac{3}{9}\)
(D) \(\frac{3}{12}\)
Answer:
\(\frac{3}{4}\)
Explanation:
One dozen cookies mean 12 cookies and she gave 6 cookies to her teacher and 3 cookies to her friend. Therefore total she gave 9 cookies to her friends. Hence fraction is equivalent to the number of cookies Maria gave away is \(\frac{3}{4}\).
Question 18.
Multi-Step Pete, Joe, and Blake shared a large pizza. The pizza was cut into eight pieces. Pete ate two pieces, Joe ate two pieces, and Blake ate one piece. Which fraction is equivalent to the amount of pizza that was eaten by all the boys?
(A) \(\frac{8}{5}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{8}{13}\)
(D) \(\frac{5}{8}\)
Answer:
\(\frac{5}{8}\)
Explanation:
Pete ate two pieces, Joe ate two pieces and Blake ate one piece. Therefore three persons ate 5 pieces of pizza. The \(\frac{5}{8}\) fraction is equivalent to the amount of pizza that was eaten by all the boys.