Refer to our Texas Go Math Grade 3 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 3 Lesson 2.4 Answer Key Fractions on a Number Line.
Texas Go Math Grade 3 Lesson 2.4 Answer Key Fractions on a Number Line
Essential Question
How can you represent and locate fractions on a number line?
Unlock the problem
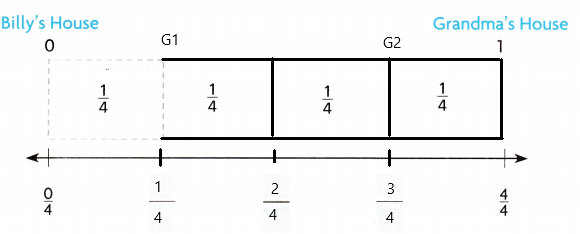
Billy’s family is traveling from his house to his grandma’s house. They stop at gas stations when they are \(\frac{1}{4}\) and \(\frac{3}{4}\) of the way there. How can he represent those distances on a number line?
You can use a number line to show fractions. The length from one whole number to the next whole number represents one whole. The line can be divided into any number of equal parts, or lengths.
Math Idea
A point on a number line shows the endpoint of a length, or distance, from zero. A number or fraction can name the distance.
Activity Locate fractions on a number line.

Step 1
Divide the line into four equal lengths, or fourths. Place four \(\frac{1}{4}\)-fraction strips end-to-end above the line to help.
Step 2
At the end of each strip, draw a mark on the line.
Step 3
Count the fourths from zero to 1 to label the distances from zero.
Step 4
Think: \(\frac{1}{4}\) is 1 out of 4 equal lengths.
Draw a point at \(\frac{1}{4}\) to represent the distance from 0 to \(\frac{1}{4}\). Label the point G1
Step 5
Think: \(\frac{3}{4}\) is 3 out of 4 equal lengths.
Draw a point at \(\frac{3}{4}\) to represent the distance from 0 to \(\frac{3}{4}\). Label the point G2
Answer:
Example
Complete the number line to name the point.
Materials ![]() color pencils, fraction strips
color pencils, fraction strips
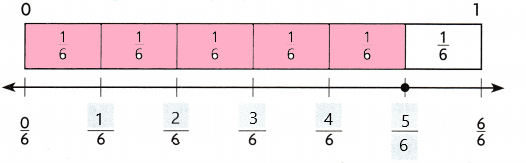
Write the fraction that names the point on the number line.
Think: This number line is divided into six equal lengths or sixths.
The length of one equal part is ___.

Shade the fraction strip diagram to show the location of the point.
There are ___ out of ___ equal lengths shaded.
The shaded length shows \(\frac{5}{6}\)
So, __ names the point.
Answer:
The length of one equal part is \(\frac{1}{6}\)
There are 5 out of 6 equal lengths shaded.
So, \(\frac{5}{6}\) names the point.
Explanation:
Share and Show
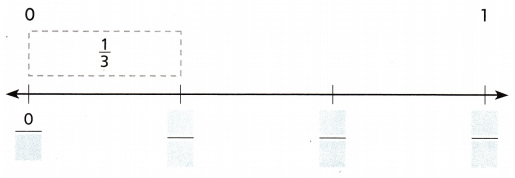
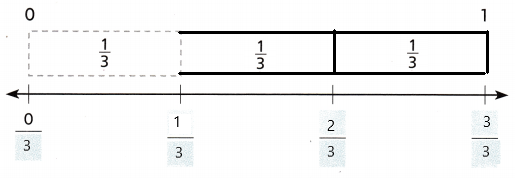
Question 1.
Use fraction strips to complete. Draw a point to show \(\frac{2}{3}\).
Answer:
I have pointed out to show the given fraction.
Explanation:
Math Talk
Mathematical Processes
Explain how you would use fraction strips to model on a number line.
Write the fraction that names the point.

Question 2.
Point A ____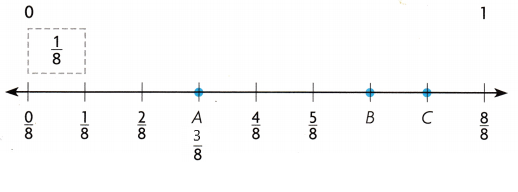
Answer:
Point A is \(\frac{3}{8}\)
Explanation:
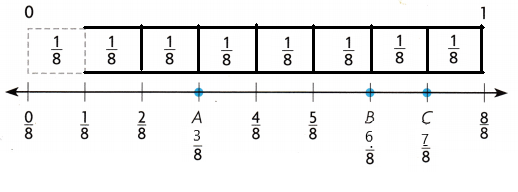
Question 3.
Point B ____
Answer:
Point B is \(\frac{6}{8}\)
Explanation:
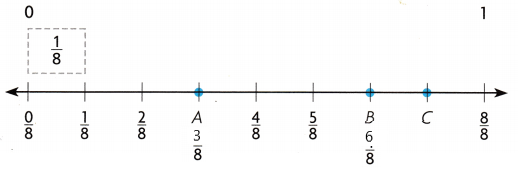
Question 4.
Point C ____
Answer:
Point C is \(\frac{7}{8}\)
Explanation:

Unlock the Problem
Question 5.
Multi-Step Javia ran 8 laps around a track to run a total of 1 mile on Monday. How many laps will she need to run on Tuesday to run \(\frac{3}{8}\) of a mile?
(A) 1
(B) 3
(C) 6
(D) 8
Answer:
3
Explanation:
Javia runs 1 mile in 8 laps.
3 times \(\frac{3}{8}\) = \(\frac{3}{8}\)
So when she runs \(\frac{3}{8}\) of a mile, she’s run 3 laps.
a. What do you need to find?
Answer:
We need to find the number of laps Javia will need to run.
b. Explain How will you use what you know about number lines to help you solve the problem?
Answer:
I will use the number line to count the number of laps in \(\frac{3}{8}\) of a mile.
c. H.O.T. Make a model to solve the problem.

Answer:
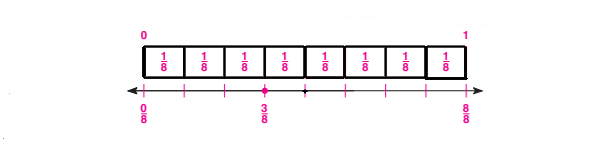
d. Complete the sentences.
There are ___ laps in 1 mile. Each lap represents ___ of a mile. ___ laps represent the distance of three eighths of a mile. So, Javia will need to run ___ laps to run \(\frac{3}{8}\) of a mile.
Answer:
There are 8 laps in 1 mile.
Each lap represents \(\frac{3}{8}\) of a mile.
Three laps represent the distance of three eighths of a mile.
So, Javia will need to run 3 laps to run \(\frac{3}{8}\) of a mile.
e. Fill in the bubble for the correct answer choice above.
Answer:
3
Explanation:
she runs \(\frac{3}{8}\) of a mile, she’s run 3 laps.
Question 6.
H.O.T. Write the missing fractions for the number line.
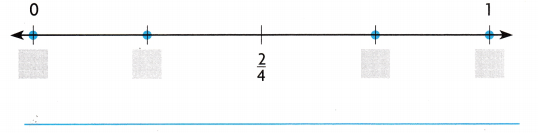
Answer:
\(\frac{0}{4}\), \(\frac{1}{4}\), \(\frac{3}{4}\) and \(\frac{4}{4}\).
Explanation:
Daily Assessment Task
Fill in the bubble for the correct answer choice.
Question 7.
Representations The point on the number line shows how far down the field a player ran in the final play of a football game. Which fraction tells how far the player ran down the field?

(A) \(\frac{2}{4}\)
(B) \(\frac{0}{4}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{4}{4}\)
Answer:
\(\frac{4}{4}\)
Explanation:
The fraction \(\frac{4}{4}\) tells how far the player ran down the field.
Question 8.
Use Diagrams Taylor rides the bus to school. There are bus stops at \(\frac{1}{6}\) and \(\frac{3}{6}\) of the way there. Which number line shows these distances?

Answer:
Option B
Explanation:
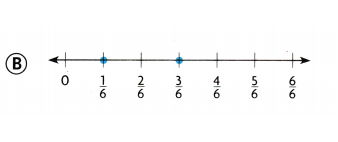
Question 9.
Multi-Step Jon uses one tank of gas to make six trips to his brother’s house. How many trips can he make on \(\frac{2}{6}\) of a tank of gas?
(A) 1
(B) 3
(C) 6
(D) 2
Answer:
2
Explanation:
Jon used one tank of gas to make six trips.
Texas Test Prep
Question 10.
Which fraction names point F on the number line?

(A) \(\frac{6}{6}\)
(B) \(\frac{2}{6}\)
(C) \(\frac{6}{2}\)
(D) \(\frac{1}{6}\)
Answer:
\(\frac{2}{6}\)
Explanation:
The fraction \(\frac{2}{6}\) names point F on the number line.
Texas Go Math Grade 3 Lesson 2.4 Homework and Practice Answer Key
Write the fraction that names the point on the number line.

Question 1.
point A
_____
Answer:
Point A is \(\frac{2}{6}\)
Explanation:
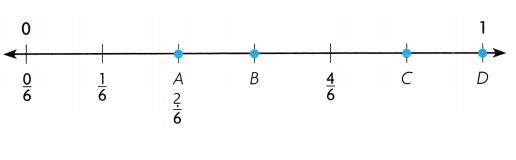
Question 2.
point B
_____
Answer:
Point B is \(\frac{3}{6}\)
Explanation:

Question 3.
point C
____
Answer:
Point C is \(\frac{5}{6}\)
Explanation:
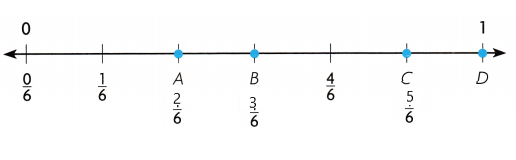
Question 4.
point D
Answer:
Point D is \(\frac{6}{6}\)
Explanation:

Use fraction strips to help you complete the number line.
Then locate and draw a point for the fraction.
Question 5.
\(\frac{2}{3}\)
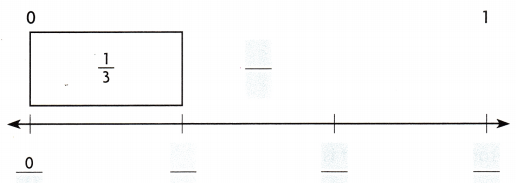
Answer:
I have located and drawn a point for the fraction
Explanation:

Problem Solving
Question 6.
There is a walking trail at the park. Four laps around the trail is a distance of 1 mile. How many laps does it take to walk \(\frac{3}{4}\) mile?
Answer:
3 laps
Explanation:
We need to determine how many laps would it take to walk \(\frac{3}{4}\) mile now we simply needed to multiply \(\frac{3}{4}\) by 4.
\(\frac{3}{4}\) × 4
\(\frac{12}{4}\)
3 laps.
Question 7.
How many laps does it take to walk \(\frac{1}{4}\) mile?
Answer:
1 lap
Explanation:
\(\frac{1}{4}\) × 4
1 lap
It takes 1 lap to walk \(\frac{1}{4}\) mile.
Lesson Check
Texas Test Prep
Fill in the bubble completely to show your answer.
Question 8.
Jen rides a bike on a bike path. She stops at \(\frac{3}{8}\) and \(\frac{5}{8}\) of the total length of the path. Which number line shows these distances?
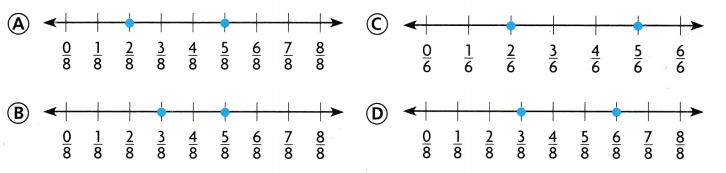
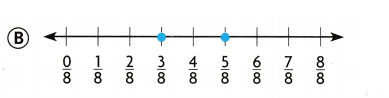
Answer:
Option B
Explanation:
Question 9.
The point on the number line shows where the home football team lines up for the next play. Which fraction shows how far down the field the team is?
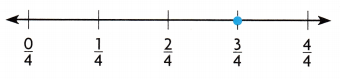
(A) \(\frac{1}{4}\)
(B) \(\frac{2}{4}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{4}{4}\)
Answer:
\(\frac{1}{4}\)
Explanation:
1-\(\frac{3}{4}\) = \(\frac{1}{4}\)
The \(\frac{1}{4}\) fraction shows how far down the field the team is.
Question 10.
Multi-Step Mrs. Foster pours six cups of lemonade from a full pitcher. How many cups can she pour from a pitcher that is full?
(A) 6 cups
(B) 4 cups
(C) 3 cups
(D) 5 cups
Answer:
5 cups
Explanation:
Mrs. Foster pours six cups of lemonade from a full pitcher. If \(\frac{6}{6}\) full pitcher pours 6 cups, then \(\frac{5}{6}\) full pitcher would pour 5 cups.
Use fraction strips to help you complete the number line. Then locate and draw a point for the fraction.
Question 11.
\(\frac{5}{6}\)

Answer:
I have located and drawn a point for the fraction given.
Explanation:
