Refer to our Texas Go Math Grade 3 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 3 Lesson 16.5 Answer Key Area of Combined Rectangles.
Texas Go Math Grade 3 Lesson 16.5 Answer Key Area of Combined Rectangles
Unlock the Problem
Anna’s rug has side lengths of 4 feet and 9 feet. What is the area of Anna’s rug?

Activity
Materials; square tiles
STEP 1:
Use square tiles to model 4 × 9.
STEP 2:
Draw a rectangle on grid paper to show your model.
STEP 3:
Draw a vertical line to break apart the model to make two smaller rectangles.
The side length 9 is broken into ___________ plus __________.
STEP 4:
Find the area of each of the two smaller rectangles.
Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
STEP 5:
Add the products to find the total area.
_________ + _________ = ___________ square feet
STEP 6:
Check your answer by counting the number of square feet.
__________ square feet
So, the area of Anna’s rug is ____________ square feet.
Answer:
STEP 1:
Use square tiles to model 4 × 9.
STEP 2:
Draw a rectangle on grid paper to show your model.
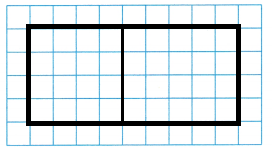
STEP 3:
Draw a vertical line to break apart the model to make two smaller rectangles.
The side length 9 is broken into 4 plus 5
STEP 4:
Find the area of each of the two smaller rectangles.
Rectangle 1: 4 × 4 = 16
Rectangle 2: 4 × 5 = 20
STEP 5:
Add the products to find the total area.
16 + 20 = 36 square feet
STEP 6:
Check your answer by counting the number of square feet.
36 square feet
So, the area of Anna’s rug is 36 square feet.
Math Talk
Mathematical Processes
Did you draw a line in the same place as your classmates? Explain why you found the same total area.
Answer:
Connect Using the Distributive Property, you found that you could break apart a rectangle into smaller rectangles, and combine the area of each smaller rectangle to find the total area.

How can you break apart this figure into rectangles to find its area?
One Way Use a horizontal line.

STEP 1:
Write a multiplication equation for each rectangle.
Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
STEP 2:
Add the products to find the total area.
_________ + __________ = __________ square units
Another Way Use a vertical line.

STEP 1:
Write a multiplication equation for each rectangle.
Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
STEP 2:
Add the products to find the total area.
_________ + __________ = __________ square units
So, the area is _________ square units.
Answer:
One Way Use a horizontal line.

STEP 1:
Write a multiplication equation for each rectangle.
Rectangle 1: 3 × 7 = 21
Rectangle 2: 3 × 3 = 9
STEP 2:
Add the products to find the total area.
21 + 9 = 30 square units
Another Way Use a vertical line.

STEP 1:
Write a multiplication equation for each rectangle.
Rectangle 1: 6 × 3 = 18
Rectangle 2: 3 × 4 = 12
STEP 2:
Add the products to find the total area.
18 + 12 = 30 square units
So, the area is 30 square units.
Math Talk
Mathematical Processes
Explain how you can check your answer.
Answer:
By counting the square units
we can find the answer
Share and Show
Question 1.
Draw a line to break apart the figure into rectangles. Find the total area of the figure.
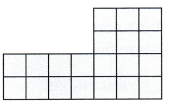
Think: I can draw vertical or horizontal lines to break apart the figure to make rectangles.
Write a multiplication equation for each rectangle.
Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
_________ + __________ = __________ square units
Answer:
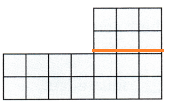
Explanation:
Rectangle 1: 2 × 3 = 6
Rectangle 2: 2 × 7 = 14
6 + 14 = 30 square units
Math Talk
Mathematical Processes
Which problem can you solve using the Distributive Property? Explain.
Answer:
Finding the area of irregular shapes.
Draw a line to break apart the figure into rectangles Then find the area. Show your multiplication and addition equations.
Question 2.

Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
_________ + __________ = __________ square units
Answer:
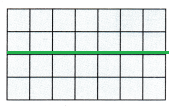
Explanation:
Rectangle 1: 2 × 7 = 14
Rectangle 2: 2 × 7 = 14
14 + 14 = 28 square units
Question 3.
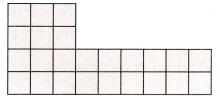
Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
_________ + __________ = __________ square units
Answer:
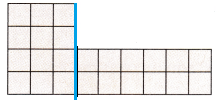
Explanation:
Rectangle 1: 4 × 3 = 12
Rectangle 2: 2 x 6 = 12
12 + 12 = 24 square units
Problem Solving
Question 4.
Multi-Step Connect A model of Lee School’s Media Center is shown at the right. Each unit square is 1 square yard. Draw a line to break apart the figure into rectangles. What is the total area of the media center?
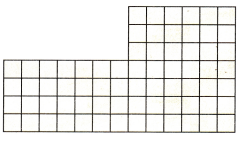
Answer:
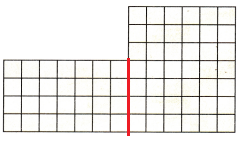
Explanation:
4 x 7 = 28
7 x 6 = 42
28 + 42 = 70
70 is the total area of the media center.
Question 5.
H.O.T. Multi-Step Apply A builder uses glass bricks shaped like cubes for a playroom wall. Draw a line to break apart the figure into rectangles. Find the area of the wall. What if the height of the wall is 8 feet and the glass area must be a rectangle? How many bricks will be left over?
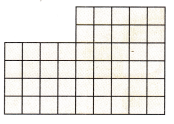
Answer:
Explanation:
The area is
2 x 5 = 10
4 x 9 = 36
36 + 10 = 46
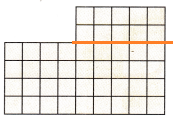
Question 6.
H.O.T. Multi-Step Explain how to break apart the figure to find the area.

Answer:

Explanation:
The area of figure is
6 x 3 = 18
3 x 5 = 15
7 x 3 = 21
18 + 15 + 21 = 54
54 is the total area
Daily Assessment Task
Fill in the bubble for the correct answer choice.
Question 7.
Max and Josh are playing Tic-Tac-Toe. Each unit square is 100 square centimeters. What is the area of the game board that they have used so far?
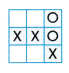
(A) 100 square centimeters
(B) 10 square centimeters
(C) 500 square centimeters
(D) 50 square centimeters
Answer: C
5 x 100 = 500 square centimeters
Explanation:
500 is the area of the game board that they have used so far.
Question 8.
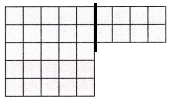
Multi-Step Mike is helping his uncle pave a parking lot. Each unit square is 1 square meter. How many square meters do they need to pave?
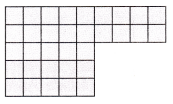
(A) 45 square meters
(B) 33 square meters
(C) 35 square meters
(D) 28 square meters
Answer: B
Explanation:
5 x 5 = 25
2 x 4 = 8
25 + 8 = 33
Question 9.
Multi-Step Callie is building a backyard pond and garden. She draws her design on grid paper. Each unit square is 1 square foot. The blue squares are pond and the green squares are garden. How many more square feet of garden are there than square feet of pond?

(A) 2 square feet
(B) 16 square feet
(C) 8 square feet
(D) 24 square feet
Answer:
4 x 2 = 8 is pond
4 x 4 = 16 is garden
16 – 8 = 8 more square feet of garden are there than square feet of pond.
Texas Test Prep
Question 10.
Pete drew a diagram of his backyard on grid paper. Each unit square is 1 square meter. The area surrounding the patio is grass. How many square meters of grass are in his backyard?

(A) 4 square meters
(B) 30 square meters
(C) 26 square meters
(D) 18 square meters
Answer: C
Explanation:
5 x 6 = 30
30 – 4 = 26 square meters of grass are in his backyard
Texas Go Math Grade 3 Lesson 16.5 Homework and Practice Answer Key
Use the Distributive Property to find the area, or draw a line to break apart the figure into rectangles. Show your multiplication and addition equations.
Question 1.

Rectangle 1: _________ × ___________ = ___________
Rectangle 2: _________ × ___________ = ____________
_________ + __________ = __________ square units
Answer:

Explanation:
Rectangle 1: 4 x 4 = 16
Rectangle 2: 2 x 4 = 8
16 + 8 = 24 square units
Question 2.

___________ square units
Answer:
7 x 5 = 35
Explanation:
35 square units
Problem Solving
Question 3.
Mr. Franklin’s patio ¡s shown at the right. Each unit square is 1 square foot. Draw a line to break apart the shape into rectangles. What ¡s the total area of Mr. Fank1in’s patio?

Answer:
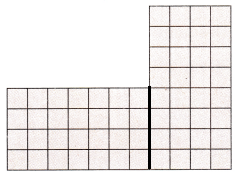
Explanation:
4 x 7 = 28
8 x 4 = 32
28 + 32 = 60 ¡s the total area of Mr. Fank1in’s patio
Question 4.
Ms. Ferrara has a rectangular kitchen with a pantry closet. Each unit square is 1 square foot. Draw a line to break apart the shape into rectangles. What is the total area of Ms. Ferrara’s kitchen?

Answer:

Explanation:
The area is
6 x 6 = 36
11 x 3 = 33
36 + 33 = 69 is the total area of Ms. Ferrara’s kitchen
Lesson Check
Fill in the bubble completely to show your answer.
Question 5.
Anya is building a wooden deck. The diagram shows the plan. Each unit square is 1 square meter. How many square meters is Anya’s deck?

(A) 40 square meters
(B) 34 square meters
(C) 25 square meters
(D) 30 square meters
Answer: B

Explanation:
3 x 3 = 9
5 x 5 = 25
25 + 9 = 34 square meters is Anya’s deck.
Question 6.
Opal creates a tile design. Each unit is 1 square inch.

How many square inches is Opal’s design?
(A) 22 square inches
(B) 16 square inches
(C) 18 square inches
(D) 28 square inches
Answer: A
4 x 2 = 8
2 x 3 = 6
4 x 2 = 8
8 + 6 + 8 = 22 square inches is Opal’s design
Question 7.
Multi-Step The shaded part of the diagram shows the squares that have game pieces on them for Team A. The board for Team B has 4 fewer game pieces on the board. Each unit is 1 square inch.

How much of Team B’s board is covered?
(A) 24 square inches
(B) 16 square inches
(C) 20 square inches
(D) 36 square inches
Answer:

Explanation:
4 x 2 = 8
2 x 2 = 4
8 + 4 = 12
4 x 2 = 8
12 + 8 = 20 is shaded part
2 x 2 = 4
4 x 3 = 12
12 + 4 = 16 The board for Team B has 4 fewer game pieces on the board. Each unit is 1 square inch.
16 – 4 = 12
Question 8.
Multi-Step Nora is planting a garden. The shaded area of the garden is tomato plants and the white area is corn. Each unit is 1 square foot. How many more square feet of tomatoes are there than square feet of corn in Nora’s garden?

(A) 24 square feet
(B) 12 square feet
(C) 18 square feet
(D) 6 square feet
Answer: D
6 x 4 = 24 is shaded part
6 x 3 = 18 is unshaded part
24 – 18 = 6 more square feet of tomatoes are there than square feet of corn in Nora’s garden.