What is the best way to learn maths? Referring to the Go Math Grade 8 Answer Key Chapter 1 Real Numbers is the best and perfect solution for all the students who want to learn maths in an easy way. Get Go Math Grade 8 Chapter 1 Real Numbers Answer Key now and begin your practice today. You will find the best and easy ways to learn maths by using Go Math Grade 8 Answer Key. Therefore, don’t look for the other source to start learning and practicing maths. Immediately open Go Math Grade 8 Chapter 1 Real Numbers Solution Key and start practicing.
Go Math Grade 8 Chapter 1 Real Numbers Answer Key
Download HMH Go Math Grade 8 Answer Key Chapter 1 Real Numbers PDF for free. Learn more about the tricks and tips to practice maths with the help of the Go Math Grade 8 Chapter 1 Real Numbers Answer Key. Find a better way to make your learning simple.
Lesson 1: Rational and Irrational Numbers
Lesson 2: Sets of real Numbers
Lesson 3: Ordering Real Numbers
Model Quiz
Mixed Review
Guided Practice – Rational and Irrational Numbers – Page No. 12
Write each fraction or mixed number as a decimal.
Question 1.
\(\frac{2}{5}\) =
Answer:
0.4
Explanation:
\(\frac{2}{5}\) = \(\frac{2 × 2}{5 × 2}\) = \(\frac{4}{10}\) = 0.4
Question 2.
\(\frac{8}{9}\) =
Answer:
0.88
Explanation:
\(\frac{8}{9}\) = \(\frac{8 × 10}{9 × 10}\) = \(\frac{80}{9 × 10}\) = \(\frac{8.88}{10}\) = 0.88
Question 3.
3 \(\frac{3}{4}\) =
Answer:
3.75
Explanation:
3 \(\frac{3}{4}\) =\(\frac{15}{4}\) = 3.75
Question 4.
\(\frac{7}{10}\) =
Answer:
0.7
Explanation:
\(\frac{7}{10}\) = 0.7
Question 5.
2 \(\frac{3}{8}\) =
Answer:
2.375
Explanation:
2 \(\frac{3}{8}\) = \(\frac{19}{8}\) = 2.375
Question 6.
\(\frac{5}{6}\) =
Answer:
0.833
Explanation:
\(\frac{5}{6}\) = \(\frac{5 × 10}{6 × 10}\) = \(\frac{50}{6 × 10}\) = \(\frac{8.33}{10}\) = 0.833
Write each decimal as a fraction or mixed number in simplest form
Question 7.
0.675
\(\frac{□}{□}\)
Answer:
\(\frac{27}{40}\)
Explanation:
\(\frac{0.675 × 1000}{1 × 1000}\) = \(\frac{675}{1000}\) = \(\frac{675/25}{1000/25}\) = \(\frac{27}{40}\)
Question 8.
5.6
______ \(\frac{□}{□}\)
Answer:
5 \(\frac{3}{5}\)
Explanation:
\(\frac{5.6 × 10}{10}\) = \(\frac{56}{10}\) = 5 \(\frac{6}{10}\) = 5 \(\frac{6/2}{10/2}\) = 5 \(\frac{3}{5}\)
Question 9.
0.44
\(\frac{□}{□}\)
Answer:
\(\frac{11}{25}\)
Explanation:
\(\frac{0.44 × 100}{1 × 100}\) = \(\frac{44}{100}\) = \(\frac{44/4}{100/4}\) = \(\frac{11}{25}\)
Question 10.
0.\(\bar{4}\)
\(\frac{□}{□}\)
Answer:
\(\frac{4}{9}\)
Explanation:
Let x = 0.\(\bar{4}\)
Now, 10x = 4.\(\bar{4}\)
10x – x = 4.\(\bar{4}\) – 0.\(\bar{4}\)
9x = 4
x = \(\frac{4}{9}\)
Question 11.
0.\(\overline { 26 } \)
\(\frac{□}{□}\)
Answer:
\(\frac{26}{99}\)
Explanation:
Let x = 0.\(\overline {26}\)
Now, 100x = 26.\(\overline{26}\)
100x – x = 26.\(\overline{26}\) – 0.\(\overline {26}\)
99x = 26
x = \(\frac{26}{99}\)
Question 12.
0.\(\overline { 325 } \)
\(\frac{□}{□}\)
Answer:
\(\frac{325}{999}\)
Explanation:
Let x = 0.\(\overline {325}\)
Now, 1000x = 325.\(\overline{325}\)
1000x – x = 325.\(\overline{325}\) – 0.\(\overline {325}\)
999x = 325
x = \(\frac{325}{999}\)
Solve each equation for x
Question 13.
x2 = 144
± ______
Answer:
x=±12
Explanation:
x2 = 144
Taking square roots on both the sides
√x2=±√144
x = ±12
Question 14.
x2 = \(\frac{25}{289}\)
± \(\frac{□}{□}\)
Answer:
x = ±\(\frac{5}{17}\)
Explanation:
x2 = \(\frac{25}{289}\)
Taking square roots on both the sides
√x2=±√\(\frac{25}{289}\)
x = ±\(\frac{5}{17}\)
Question 15.
x3 = 216
______
Answer:
x = 6
Explanation:
x3 = 216
Taking cube roots on both the sides
3√x3= 3√216
x = 6
Approximate each irrational number to two decimal places without a calculator.
Question 16.
\(\sqrt { 5 } \) ≈ ______
Answer:
2.236
Explanation:
x = \(\sqrt { 5 } \)
The 5 is in between 4 and 6
Take square root of each year
√4 < √5 < √6
2 < √5 < 3
√5 = 2.2
(2.2)² = 4.84
(2.25)² = 5.06
(2.5)³ = 5.29
A good estimate for √5 is 2.25
Question 17.
\(\sqrt { 3 } \) ≈ ______
Answer:
1.75
Explanation:
\(\sqrt { 3 } \)
1 < 3 < 4
√1 < √3 < √4
1 < √3 < 2
√3 = 1.6
(1.65)² = 2.72
(1.7)² = 2.89
(1.75)² = 3.06
A good estimate for √3 is 1.75
Question 18.
\(\sqrt { 10 } \) ≈ ______
Answer:
3.15
Explanation:
\(\sqrt { 10 } \)
9 < 10 < 16
√9 < √10 < √16
3 < √10 < 4
√10 = 3.1
(3.1)² = 9.61
(3.15)² = 9.92
(3.2)² = 10.24
A good estimate for √10 is 3.15
Question 19.
What is the difference between rational and irrational numbers?
Type below:
_____________
Answer:
Rational number can be expressed as a ration of two integers such as 5/2
Irrational number cannot be expressed as a ratio of two integers such as √13
Explanation:
A rational number is a number that can be express as the ratio of two integers. A number that cannot be expressed that way is irrational.
1.1 Independent Practice – Rational and Irrational Numbers – Page No. 13
Question 20.
A \(\frac{7}{16}\)-inch-long bolt is used in a machine. What is the length of the bolt written as a decimal?
______ -inch-long
Answer:
0.4375 inch
Explanation:
The length of the bolt is \(\frac{7}{16}\)-inch
Let, x = \(\frac{7}{16}\)
Multiplying by 125 on both nominator and denominator
x = \(\frac{7×125}{16×125}\) = \(\frac{875}{2000}\) =\(\frac{437.5}{1000}\) = 0.4375
Question 21.
The weight of an object on the moon is \(\frac{1}{6}\) its weight on Earth. Write \(\frac{1}{6}\) as a decimal.
______
Answer:
0.1666
Explanation:
The weight of the object on the moon is \(\frac{1}{6}\)
Let, x = \(\frac{1}{6}\)
Multiplying by 100 on both nominator and denominator
x = \(\frac{1×100}{6×100}\) = \(\frac{16.6}{100}\) =0.166
Question 22.
The distance to the nearest gas station is 2 \(\frac{4}{5}\) kilometers. What is this distance written as a decimal?
______
Answer:
2.8
Explanation:
The distance of the nearest gas station is 2 \(\frac{4}{5}\)
Let, x = 2 \(\frac{4}{5}\)
Multiplying by 100 on both nominator and denominator
x = 2 \(\frac{4×100}{5×100}\) = \(\frac{80}{100}\) =0.8
Question 23.
A baseball pitcher has pitched 98 \(\frac{2}{3}\) innings. What is the number of innings written as a decimal?
______
Answer:
98.6
Explanation:
A baseball pitcher has pitched 98 \(\frac{2}{3}\) innings.
98 \(\frac{2}{3}\) = 98 + 2/3
= (294/3) + (2/3)
296/3
98.6
Question 24.
A heartbeat takes 0.8 second. How many seconds is this written as a fraction?
\(\frac{□}{□}\)
Answer:
\(\frac{4}{5}\)
Explanation:
A heartbeat takes 0.8 seconds.
0.8
There are 8 tenths.
8/10 = 4/5
Question 25.
There are 26.2 miles in a marathon. Write the number of miles using a fraction.
\(\frac{□}{□}\)
Answer:
26\(\frac{1}{5}\)
Explanation:
There are 26.2 miles in a marathon.
26.2 miles
262/10
131/5
26 1/5 miles
Question 26.
The average score on a biology test was 72.\(\bar{1}\). Write the average score using a fraction.
\(\frac{□}{□}\)
Answer:
80 \(\frac{1}{9}\)
Explanation:
The average score on a biology test was 72.\(\bar{1}\).
72.\(\bar{1}\)
Let x = 72.\(\bar{1}\)
10x = 10(72.\(\bar{1}\))
10x = 721.1
-x = -0.1
9x = 721
x = 721/9
x = 80 1/9
Question 27.
The metal in a penny is worth about 0.505 cent. How many cents is this written as a fraction?
\(\frac{□}{□}\)
Answer:
\(\frac{101}{200}\)
Explanation:
The metal in a penny is worth about 0.505 cent.
0.505 cent
505 thousandths
505/1000
101/200 cents
Question 28.
Multistep An artist wants to frame a square painting with an area of 400 square inches. She wants to know the length of the wood trim that is needed to go around the painting.

a. If x is the length of one side of the painting, what equation can you set up to find the length of a side?
x2 = ______
Answer:
x² = 400
Explanation:
The area of a square is the square of its equal side, x
x² = 400
Question 28.
b. Solve the equation you wrote in part a. How many solutions does the equation have?
x = ± ______
Answer:
x = ± 20
Explanation:
Take the square root on both sides. Solve
x = ± 20
Question 28.
c. Do all of the solutions that you found in part b make sense in the context of the problem? Explain.
Type below:
_____________
Answer:
No. Both values of x do not make sense.
Explanation:
The length cannot be negative, hence negative value does not make sense.
No. Both values of x do not make sense.
Question 28.
d. What is the length of the wood trim needed to go around the painting?
P = ______ inches
Answer:
Length P = 20 + 2y
Rational and Irrational Numbers – Page No. 14
Question 29.
Analyze Relationships To find \(\sqrt { 15 } \), Beau found 32 = 9 and 42 = 16. He said that since 15 is between 9 and 16, \(\sqrt { 15 } \) must be between 3 and 4. He thinks a good estimate for \(\sqrt { 15 } \) is \(\frac { 3+4 }{ 2 } \) = 3.5. Is Beau’s estimate high, low, or correct? Explain.
_____________
Answer:
3.85
Explanation:
15 is closer to 16
√15 is closer to √16
Beau’s estimate is low.
(3.8)² = 14.44
(3.85)² = 14.82
(3.9)² = 15.21
√15 is 3.85
Question 30.
Justify Reasoning What is a good estimate for the solution to the equation x3 = 95? How did you come up with your estimate?
x ≈ ______
Answer:
x ≈ 4.55
Explanation:
3√x = 95
x = 3√95
64 < 95 < 125
Take the cube root of each number
3√64 < 3√95 < 3√125
4 < 3√95 < 5
3√95 = 4.6
(4.5)³ = 91.125
(4.55)³ = 94.20
(4.6)³ = 97.336
3√95 = 4.55
Question 31.
The volume of a sphere is 36π ft3. What is the radius of the sphere? Use the formula V = \(\frac { 4 }{ 3 } \)πr3 to find your answer.

r = ______
Answer:
r = 3
Explanation:
V = 4/3 πr³
36π = 4/3 πr³
r³ = 36π/π . 3/4
r³ = 27
r = 3√27
r = 3
FOCUS ON HIGHER ORDER THINKING
Question 32.
Draw Conclusions Can you find the cube root of a negative number? If so, is it positive or negative? Explain your reasoning.
_____________
Answer:
Yes
Explanation:
Yes. The cube root of a negative number would be negative. Because the product of three negative signs is always negative.
Question 33.
Make a Conjecture Evaluate and compare the following expressions.
\(\sqrt { \frac { 4 }{ 25 } } \) and \(\frac { \sqrt { 4 } }{ \sqrt { 25 } } \) \(\sqrt { \frac { 16 }{ 81 } } \) and \(\frac { \sqrt { 16 } }{ \sqrt { 81 } } \) \(\sqrt { \frac { 36 }{ 49 } } \) and\(\frac { \sqrt { 36 } }{ \sqrt { 49 } } \)
Use your results to make a conjecture about a division rule for square roots. Since division is multiplication by the reciprocal, make a conjecture about a multiplication rule for square roots.
Expressions are: _____________
Answer:
Evaluating and comparing
√4/25 = 2/5
√16/81 = 4/9
√36/49 = 6/7
Conjecture about a division rule for square roots
√a/√b = √(a/b)
Conjecture about a multiplication rule for square roots
√a × √b
Question 34.
Persevere in Problem Solving
The difference between the solutions to the equation x2 = a is 30. What is a? Show that your answer is correct.
_____
Answer:
30
Explanation:
x2 = a
x = ±√a
√a – (-√a) = 30
√a + √a = 30
2√a = 30
√a = 15
a = 225
x2 = 225
x = ±225
x = ±15
15 – (-15) = 15 + 15 = 30
Guided Practice – Sets of real Numbers – Page No. 18
Write all names that apply to each number.
Question 1.
\(\frac{7}{8}\)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
Question 2.
\(\sqrt { 36 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
Explanation:
\(\sqrt { 36 } \) = 6
Question 3.
\(\sqrt { 24 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
e. Irrational Numbers
Question 4.
0.75
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
Question 5.
0
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
Question 6.
−\(\sqrt { 100 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integers
Explanation:
−\(\sqrt { 100 } \) = – 10
Question 7.
5.\(\overline { 45 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
Question 8.
−\(\frac{18}{6}\)
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integers
Explanation:
−\(\frac{18}{6}\) = -3
Tell whether the given statement is true or false. Explain your choice.
Question 9.
All whole numbers are rational numbers.
i. True
ii. False
Answer:
i. True
Explanation:
All whole numbers are rational numbers.
Whole numbers are a subset of the set of rational numbers and can be written as ratio of the whole number to 1.
Question 10.
No irrational numbers are whole numbers.
i. True
ii. False
Answer:
i. True
Explanation:
True. Whole numbers are ration numbers.
Identify the set of numbers that best describes each situation. Explain your choice.
Question 11.
the change in the value of an account when given to the nearest dollar
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
c. Integer Numbers
Explanation:
The change can be a whole dollar amount and can be positive, negative or zero.
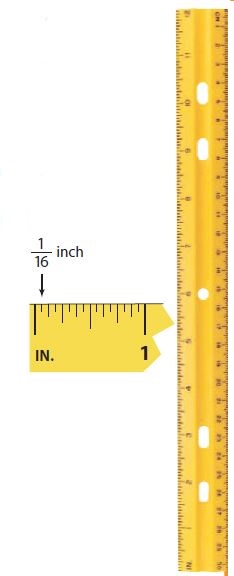
Question 12.
the markings on a standard ruler
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
b. Rational Numbers
Explanation:
The ruler is marked every 1/16t inch.
ESSENTIAL QUESTION CHECK-IN
Question 13.
What are some ways to describe the relationships between sets of numbers?
Answer:
There are two ways that we have been using until now to describe the relationships between sets of numbers
- Using a scheme or a diagram as the one on page 15.
- Verbal description, for example, “All irrational numbers are real numbers.”
1.2 Independent Practice – Sets of real Numbers – Page No. 19
Write all names that apply to each number. Then place the numbers in the correct location on the Venn diagram.
Question 14.
\(\sqrt { 9 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
Explanation:
\(\sqrt { 9 } \) = 3
Question 15.
257
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
Question 16.
\(\sqrt { 50 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
e. Irrational Numbers
Question 17.
8 \(\frac{1}{2}\)
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
Question 18.
16.6
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
Question 19.
\(\sqrt { 16 } \)
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
Explanation:
\(\sqrt { 16 } \) = 4
Identify the set of numbers that best describes each situation. Explain your choice.
Question 20.
the height of an airplane as it descends to an airport runway
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
d. Whole Numbers
Explanation:
Whole. The height of an airplane as it descents to an airport runway is a whole number greater than 0
Question 21.
the score with respect to par of several golfers: 2, – 3, 5, 0, – 1
Options:
a. Real Numbers
b. Rational Numbers
c. Integer Numbers
d. Whole Numbers
e. Irrational Numbers
Answer:
c. Integer Numbers
Explanation:
Integers. The scores are counting numbers, their opposites, and zero.
Question 22.
Critique Reasoning Ronald states that the number \(\frac{1}{11}\) is not rational because, when converted into a decimal, it does not terminate. Nathaniel says it is rational because it is a fraction. Which boy is correct? Explain.
i. Ronald
ii. Nathaniel
Answer:
ii. Nathaniel
Explanation:
Nathaniel is correct.
A fraction is a rational real number, even if it is not a terminating decimal.
Sets of real Numbers – Page No. 20
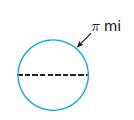
Question 23.
Critique Reasoning The circumference of a circular region is shown. What type of number best describes the diameter of the circle? Explain your answer.
Options:
a. Real Numbers
b. Rational Numbers
c. Irrational Numbers
d. Integers
e. Whole Numbers
Answer:
e. Whole Numbers
Explanation:
Circumference of the circle
A = 2πr
π = 2πr
Diameter is twice the radius
2r = 1
Whole
Question 24.
Critical Thinking A number is not an integer. What type of number can it be?
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
b. Rational Numbers
e. Irrational Numbers
Question 25.
A grocery store has a shelf with half-gallon containers of milk. What type of number best represents the total number of gallons?
Options:
a. Real Numbers
b. Rational Numbers
c. Integers
d. Whole Numbers
e. Irrational Numbers
Answer:
b. Rational Numbers
FOCUS ON HIGHER ORDER THINKING
Question 26.
Explain the Error Katie said, “Negative numbers are integers.” What was her error?
Type below:
_______________
Answer:
Her error is that she stated that all negative numbers are integers. Some negative numbers are integers such as -4 but some are not such an -0.8
Question 27.
Justify Reasoning Can you ever use a calculator to determine if a number is rational or irrational? Explain.
Type below:
_______________
Answer:
Not always.
Explanation:
Not always.
If the calculator shows a terminating decimal, the number is rational but otherwise, it is not possible as you can only see a few digits.
Question 28.
Draw Conclusions The decimal 0.\(\bar{3}\) represents \(\frac{1}{3}\). What type of number best describes 0.\(\bar{9}\) , which is 3 × 0.\(\bar{3}\)? Explain.
Type below:
_______________
Answer:
1
Explanation:
let x = 0.9999999
10x = 9.99999999
10x = 9 + 0.999999999
10x = 9 + x
9x = 9
x=1.
Question 29.
Communicate Mathematical Ideas Irrational numbers can never be precisely represented in decimal form. Why is this?
Answer:
Because irrational numbers are nonrepeating, otherwise they could be represented as a fraction. Although a potential counter-example to this claim is that some irrational numbers can only be represented in decimal form, for example, 0.1234567891011121314151617…, 0.24681012141618202224…, 0.101101110111101111101111110… are all irrational numbers.
Guided Practice – Ordering Real Numbers – Page No. 24
Compare. Write <, >, or =.
Question 1.
\(\sqrt { 3 } \) + 2 ________ \(\sqrt { 3 } \) + 3
Answer:
\(\sqrt { 3 } \) + 2 < \(\sqrt { 3 } \) + 3
Explanation:
\(\sqrt { 3 } \) is between 1 and 2
\(\sqrt { 3 } \) + 2 is between 3 and 4
\(\sqrt { 3 } \) + 3 is between 4 and 5
\(\sqrt { 3 } \) + 2 < \(\sqrt { 3 } \) + 3
Question 2.
\(\sqrt { 11 } \) + 15 _______ \(\sqrt { 8 } \) + 15
Answer:
\(\sqrt { 11 } \) + 15 > \(\sqrt { 8 } \) + 15
Explanation:
\(\sqrt { 11 } \) is between 3 and 4
\(\sqrt { 8 } \) is between 2 and 3
\(\sqrt { 11 } \) + 15 is between 18 and 19
\(\sqrt { 8 } \) + 15 is between 17 and 18
\(\sqrt { 11 } \) + 15 > \(\sqrt { 8 } \) + 15
Question 3.
\(\sqrt { 6 } \) + 5 _______ 6 + \(\sqrt { 5 } \)
Answer:
\(\sqrt { 6 } \) + 5 < 6 + \(\sqrt { 5 } \)
Explanation:
\(\sqrt { 6 } \) is between 2 and 3
\(\sqrt { 5 } \) is between 2 and 3
\(\sqrt { 6 } \) is between 7 and 8
\(\sqrt { 5 } \) is between 8 and 9
\(\sqrt { 6 } \) + 5 < 6 + \(\sqrt { 5 } \)
Question 4.
\(\sqrt { 9 } \) + 3 _______ 9 + \(\sqrt { 3 } \)
Answer:
\(\sqrt { 9 } \) + 3 < 9 + \(\sqrt { 3 } \)
Explanation:
\(\sqrt { 9 } \) + 3
9 + \(\sqrt { 3 } \)
\(\sqrt { 3 } \) is between 1 and 2
\(\sqrt { 9 } \) + 3 = 3 + 3 = 6
9 + \(\sqrt { 3 } \) is between 10 and 11
\(\sqrt { 9 } \) + 3 < 9 + \(\sqrt { 3 } \)
Question 5.
\(\sqrt { 17 } \) – 3 _______ -2 + \(\sqrt { 5 } \)
Answer:
\(\sqrt { 17 } \) – 3 > -2 + \(\sqrt { 5 } \)
Explanation:
\(\sqrt { 17 } \) is between 4 and 5
\(\sqrt { 5 } \) is between 2 and 3
\(\sqrt { 17 } \) – 3 is between 1 and 2
-2 + \(\sqrt { 5 } \) is between 0 and 1
\(\sqrt { 17 } \) – 3 > -2 + \(\sqrt { 5 } \)
Question 6.
10 – \(\sqrt { 8 } \) _______ 12 – \(\sqrt { 2 } \)
Answer:
10 – \(\sqrt { 8 } \) < 12 – \(\sqrt { 2 } \)
Explanation:
\(\sqrt { 8 } \) is between 2 and 3
\(\sqrt { 2 } \) is between 1 and 2
10 – \(\sqrt { 8 } \) is between 8 and 7
12 – \(\sqrt { 2 } \) is between 11 and 10
10 – \(\sqrt { 8 } \) < 12 – \(\sqrt { 2 } \)
Question 7.
\(\sqrt { 7 } \) + 2 _______ \(\sqrt { 10 } \) – 1
Answer:
\(\sqrt { 7 } \) + 2 > \(\sqrt { 10 } \) – 1
Explanation:
\(\sqrt { 7 } \) is between 2 and 3
\(\sqrt { 10 } \) is between 3 and 4
\(\sqrt { 7 } \) + 2 is between 4 and 5
\(\sqrt { 10 } \) – 1 is between 2 and 3
\(\sqrt { 7 } \) + 2 > \(\sqrt { 10 } \) – 1
Question 8.
\(\sqrt { 17 } \) + 3 _______ 3 + \(\sqrt { 11 } \)
Answer:
\(\sqrt { 17 } \) + 3 > 3 + \(\sqrt { 11 } \)
Explanation:
\(\sqrt { 17 } \) is between 4 and 5
\(\sqrt { 11 } \) is between 3 and 4
\(\sqrt { 17 } \) + 3 is between 7 and 8
3 + \(\sqrt { 11 } \) is between 6 and 7
\(\sqrt { 17 } \) + 3 > 3 + \(\sqrt { 11 } \)
Question 9.
Order \(\sqrt { 3 } \), 2 π, and 1.5 from least to greatest. Then graph them on the number line.
\(\sqrt { 3 } \) is between _________ and _____________ , so \(\sqrt { 3 } \) ≈ ____________.
π ≈ 3.14, so 2 π ≈ _______________.

From least to greatest, the numbers are ______________, _____________________ ,_________________.
Type below:
___________
Answer:
1.5, \(\sqrt { 3 } \), 2 π
Explanation:
\(\sqrt { 3 } \) is between 1.7 and 1.75
π = 3.14; 2 π = 6.28
![]()
1.5, \(\sqrt { 3 } \), 2 π
Question 10.
Four people have found the perimeter of a forest using different methods. Their results are given in the table. Order their calculations from greatest to least.

Type below:
___________
Answer:
\(\sqrt { 17 } \) – 2, 1+ π/2, 2.5, 12/5
Explanation:
\(\sqrt { 17 } \) – 2
\(\sqrt { 17 } \) is between 4 and 5
Since, 17 is closer to 16, the estimated value is 4.1
1+ π/2
1 + (3.14/2) = 2.57
12/5 = 2.4
2.5
\(\sqrt { 17 } \) – 2, 1+ π/2, 2.5, 12/5
ESSENTIAL QUESTION CHECK-IN
Question 11.
Explain how to order a set of real numbers.
Type below:
___________
Answer:
Evaluate the given numbers and write in decimal form. Plot on number line and arrange the numbers accordingly.
Independent Practice – Ordering Real Numbers – Page No. 25
Order the numbers from least to greatest.
Question 12.
\(\sqrt { 7 } \), 2, \(\frac { \sqrt { 8 } }{ 2 } \)
Type below:
____________
Answer:
\(\frac { \sqrt { 8 } }{ 2 } \), 2, \(\sqrt { 7 } \)
Explanation:
\(\sqrt { 7 } \), 2, \(\frac { \sqrt { 8 } }{ 2 } \)
\(\sqrt { 7 } \) is between 2 and 3
Since 7 is closer to 9, (2.65)² = 7.02, hence the estimated value is 2.65
\(\frac { \sqrt { 8 } }{ 2 } \)
\(\sqrt { 8 } \) is between 2 and 3
Since 8 is closer to 9, (2.85)² = 8.12, hence the estimated value is 2.85
2.85/2 = 1.43
![]()
\(\frac { \sqrt { 8 } }{ 2 } \), 2, \(\sqrt { 7 } \)
Question 13.
\(\sqrt { 10 } \), π, 3.5
Type below:
____________
Answer:
π, \(\sqrt { 10 } \), 3.5
Explanation:
\(\sqrt { 10 } \), π, 3.5
\(\sqrt { 10 } \) is between 3 and 4
Since, 10 is closer to 9, (3.15)² = 9.92, hence the estimated value is 3.15
π = 3.14
3.5
![]()
π, \(\sqrt { 10 } \), 3.5
Question 14.
\(\sqrt { 220 } \), −10, \(\sqrt { 100 } \), 11.5
Type below:
____________
Answer:
-10, √100, 11.5, √220
Explanation:
\(\sqrt { 220 } \), −10, \(\sqrt { 100 } \), 11.5
196 < 220 < 225
√196 < √220 < √225
14 < √220 < 15
√220 = 14.5
√100 = 10
![]()
-10, √100, 11.5, √220
Question 15.
\(\sqrt { 8 } \), −3.75, 3, \(\frac{9}{4}\)
Type below:
____________
Answer:
−3.75, \(\frac{9}{4}\), \(\sqrt { 8 } \)
Explanation:
\(\sqrt { 8 } \), −3.75, 3, \(\frac{9}{4}\)
\(\sqrt { 8 } \) is between 2 and 3
Since, 8 is closer to 9, (2.85)² = 8.12, hence the estimated value is 2.85
-3.75 = 3
9/4 = 2.25
![]()
−3.75, \(\frac{9}{4}\), \(\sqrt { 8 } \)
Question 16.
Your sister is considering two different shapes for her garden. One is a square with side lengths of 3.5 meters, and the other is a circle with a diameter of 4 meters.
a. Find the area of the square.
_______ m2
Answer:
(3.5)² = 12.25
Explanation:
Area of the square = x²
Area = (3.5)² = 12.25
Question 16.
b. Find the area of the circle.
_______ m2
Answer:
π(2)² = 12.56
Explanation:
Area of the circle = πr² where r = d/2 = 4/2 = 2
Area = π(2)² = 12.56
Question 16.
c. Compare your answers from parts a and b. Which garden would give your sister the most space to plant?
___________
Answer:
12.25 < 12.56
The circle will give more space
Question 17.
Winnie measured the length of her father’s ranch four times and got four different distances. Her measurements are shown in the table.
a. To estimate the actual length, Winnie first approximated each distance to the nearest hundredth. Then she averaged the four numbers. Using a calculator, find Winnie’s estimate.
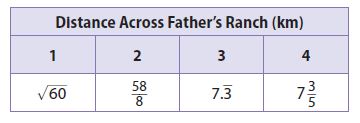
______
Answer:
7.4815
Explanation:
\(\sqrt { 60 } \) = 7.75
58/8 = 7.25
7.3333
7 3/5 = 7.60
Average = (7.75 + 7.25 + 7.33 + 7.60)/4 = 7.4815
Question 17.
b. Winnie’s father estimated the distance across his ranch to be \(\sqrt { 56 } \) km. How does this distance compare to Winnie’s estimate?
____________
Answer:
They are nearly identical
Explanation:
\(\sqrt { 56 } \) = 7.4833
They are nearly identical
Give an example of each type of number.
Question 18.
a real number between \(\sqrt { 13 } \) and \(\sqrt { 14 } \)
Type below:
____________
Answer:
A real number between \(\sqrt { 13 } \) and \(\sqrt { 14 } \)
Example: 3.7
Explanation:
\(\sqrt { 13 } \) = 3.61
\(\sqrt { 13 } \) = 3.74
A real number between \(\sqrt { 13 } \) and \(\sqrt { 14 } \)
Example: 3.7
Question 19.
an irrational number between 5 and 7
Type below:
____________
Answer:
An irrational number between 5 and 7
Example: \(\sqrt { 29 } \)
Explanation:
5² = 25 and 7² = 49
An irrational number between 5 and 7
Example: \(\sqrt { 29 } \)
Ordering Real Numbers – Page No. 26
Question 20.
A teacher asks his students to write the numbers shown in order from least to greatest. Paul thinks the numbers are already in order. Sandra thinks the order should be reversed. Who is right?

_____________
Answer:
Neither are correct
Explanation:
\(\sqrt { 115 } \), 115/11, 10.5624
\(\sqrt { 115 } \) is between 10 and 11
Since, 115 is closer to 121, (10.7)² = 114.5, hence the estimated value is 10.7
115/11 = 10.4545
10.5624
Neither are correct
Question 21.
Math History
There is a famous irrational number called Euler’s number, symbolized with an e. Like π, its decimal form never ends or repeats. The first few digits of e are 2.7182818284.
a. Between which two square roots of integers could you find this number?
Type below:
_____________
Answer:
The square of e lies between 7 and 8
2.718281828
(2.72)² = 7.3984
Hence, it lies between \(\sqrt { 7 } \) = 2.65 and \(\sqrt { 8 } \) = 2.82
Question 21.
b. Between which two square roots of integers can you find π?
Type below:
_____________
Answer:
3.142
(3.14)² = 9.8596
Hence. it lies between \(\sqrt { 9 } \) = 3 and \(\sqrt { 10 } \) = 3.16
H.O.T.
FOCUS ON HIGHER ORDER THINKING
Question 22.
Analyze Relationships
There are several approximations used for π, including 3.14 and \(\frac{22}{7}\). π is approximately 3.14159265358979 . . .
a. Label π and the two approximations on the number line.
![]()
Type below:
_____________
Answer:
![]()
Question 22.
b. Which of the two approximations is a better estimate for π? Explain.
Type below:
_____________
Answer:
As we can see from the number line, 22/7 is closer to π, so we can conclude that 22/7 is a better estimation for π.
Question 22.
c. Find a whole number x so that the ratio \(\frac{x}{113}\) is a better estimate for π than the two given approximations.
Type below:
_____________
Answer:
355/113 is a better estimation for π, because 355/113 = 3.14159292035 = 3.14159265358979 = π
Question 23.
Communicate Mathematical Ideas
What is the fewest number of distinct points that must be graphed on a number line, in order to represent natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers? Explain.
_______ points
Answer:
2 points
Explanation:
There need to be plotting of at least 2 points because a rational number can never be equal to an irrational number. So let’s say 5 points are the same among six but the 6th will be different as there both rational numbers and irrational numbers included.
Question 24.
Critique Reasoning
Jill says that 12.\(\bar{6}\) is less than 12.63. Explain her error.
Type below:
_____________
Answer:
12.\(\bar{6}\) = 12.666
12.\(\bar{6}\) > 12.63
1.1 Rational and Irrational Numbers – Model Quiz – Page No. 27
Write each fraction as a decimal or each decimal as a fraction.
Question 1.
\(\frac{7}{20}\)
_______
Answer:
0.35
Explanation:
\(\frac{7}{20}\) = 0.35
Question 2.
1.\(\overline { 27} \)
______ \(\frac{□}{□}\)
Answer:
1\(\frac{28}{99}\)
Explanation:
1.\(\overline { 27} \)
x = 1.\(\overline { 27} \)
100x = 100(1.\(\overline { 27} \))
100x = 127(\(\overline { 27} \))
x = .\(\overline { 27} \)
99x = 127
x = 127/99
x = 1 28/99
Question 3.
1 \(\frac{7}{8}\)
______
Answer:
1.875
Explanation:
1 \(\frac{7}{8}\)
1 + 7/8
8/8 + 7/8
15/8 = 1.875
Solve each equation for x.
Question 4.
x2 = 81
± ______
Answer:
± 9
Explanation:
x2 = 81
x = ± 81
x = ± 9
Question 5.
x3 = 343
______
Answer:
x = 7
Explanation:
x3 = 343
x = 7
Question 6.
x2 = \(\frac{1}{100}\)
± \(\frac{□}{□}\)
Answer:
± \(\frac{1}{10}\)
Explanation:
x2 = \(\frac{1}{100}\)
x = ± \(\frac{1}{10}\)
Question 7.
A square patio has an area of 200 square feet. How long is each side of the patio to the nearest 0.05?
______ feet
Answer:
14.15 feet
Explanation:
The area of a square is found by multiplying the side of the square by itself. Therefore, to find the side of the square, we have to take the square root of the area.
Let’s denote with A the area of the patio and with s each side of the square.
We have:
A = 200
A = s.s
s = \(\sqrt { A } \) = \(\sqrt { 200 } \)
Following the steps as in “Explore Activity” on page 9, we can make an estimation for the irrational number:
196 < 200 < 225
\(\sqrt { 196 } \) < \(\sqrt { 200 } \) < \(\sqrt { 225 } \)
14 < \(\sqrt { 200 } \) < 15
We see that 200 is much closer to 196 than to 225, therefore the square root of it should be between 14 and 14.5. To make a better estimation, we pick some numbers between 14 and 14.5 and calculate their squares:
(14.1)² = 198.81
(14.2)² = 201.64
14.1 < \(\sqrt { 200 } \) < 14.2
\(\sqrt { 200 } \) = 14.15
We see that 200 is much closer to 14.1 than to 14.2, therefore the square root of it should be between 14.1 and 14.15. If we round to the nearest 0.05, we have:
s = 14.15
1.2 Sets of Real Numbers
Write all names that apply to each number.
Question 8.
\(\frac { 121 }{ \sqrt { 121 } }\)
Type below:
___________
Answer:
Rational, whole, integer, real numbers
Explanation:
\(\frac { 121 }{ \sqrt { 121 } }\)
121/11 = 11
Question 9.
\(\frac{π}{2}\)
Type below:
___________
Answer:
Irrational, real numbers
Question 10.
Tell whether the statement “All integers are rational numbers” is true or false. Explain your choice.
___________
Answer:
True
Explanation:
“All integers are rational numbers” is true, because every integer can be expressed as a fraction with a denominator equal to 1. The set of integer A a subset of rational numbers.
1.3 Ordering Real Numbers
Compare. Write <, >, or =.
Question 11.
\(\sqrt { 8 }\) + 3 _______ 8 + \(\sqrt { 3 }\)
Answer:
\(\sqrt { 8 }\) + 3 < 8 + \(\sqrt { 3 }\)
Explanation:
4 < 8 < 9
\(\sqrt { 4 }\) < \(\sqrt { 8 }\) < \(\sqrt { 9 }\)
2 < \(\sqrt { 8 }\) < 3
1 < 3 < 4
\(\sqrt { 1 }\) < \(\sqrt { 3 }\) < \(\sqrt { 4 }\)
1 < \(\sqrt { 3 }\) < 2
\(\sqrt { 8 }\) + 3 is between 5 and 6
8 + \(\sqrt { 3 }\) is between 9 and 10
\(\sqrt { 8 }\) + 3 < 8 + \(\sqrt { 3 }\)
Question 12.
\(\sqrt { 5 }\) + 11 _______ 5 + \(\sqrt { 11 }\)
Answer:
\(\sqrt { 5 }\) + 11 > 5 + \(\sqrt { 11 }\)
Explanation:
\(\sqrt { 5 }\) lies in between 2 and 3
\(\sqrt { 11 }\) lies in between 3 and 4
\(\sqrt { 5 }\) + 11 lies in between 13 and 14
5 + \(\sqrt { 11 }\) lies in between 8 and 9
\(\sqrt { 5 }\) + 11 > 5 + \(\sqrt { 11 }\)
Order the numbers from least to greatest.
Question 13.
\(\sqrt { 99 }\), π2, 9.\(\bar { 8 }\)
Type below:
_______________
Answer:
π2, 9.\(\bar { 8 }\), \(\sqrt { 99 }\)
Explanation:
\(\sqrt { 99 }\), π2, 9.\(\bar { 8 }\)
99 lies between 9² and 10²
99 is closer to 100, hence \(\sqrt { 99 }\) is closer to 10
(9.9)² = 98.01
(9.95)² = 99.0025
(10)² = 100
\(\sqrt { 99 }\) = 9.95
π² = 9.86
9.88888 = 9.89

π2, 9.\(\bar { 8 }\), \(\sqrt { 99 }\)
Question 14.
\(\sqrt { \frac { 1 }{ 25 } } \), \(\frac{1}{4}\), 0.\(\bar { 2 }\)
Type below:
____________
Answer:
\(\sqrt { \frac { 1 }{ 25 } } \), 0.\(\bar { 2 }\), \(\frac{1}{4}\)
Explanation:
\(\sqrt { \frac { 1 }{ 25 } } \), \(\frac{1}{4}\), 0.\(\bar { 2 }\)
\(\sqrt { \frac { 1 }{ 25 } } \) = 1/5 = 0.2
1/4 = 0.25
0.\(\bar { 2 }\) = 0.222 = 0.22
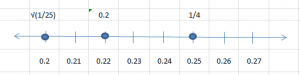
\(\sqrt { \frac { 1 }{ 25 } } \), 0.\(\bar { 2 }\), \(\frac{1}{4}\)
Essential Question
Question 15.
How are real numbers used to describe real-world situations?
Type below:
_______________
Answer:
In real-world situations, we use real numbers to count or make measurements. They can be seen as a convention for us to quantify things around, for example, the distance, the temperature, the height, etc.
Selected Response – Mixed Review – Page No. 28
Question 1.
The square root of a number is 9. What is the other square root?
Options:
a. -9
b. -3
c. 3
d. 81
Answer:
a. -9
Explanation:
We know that every positive number has two square roots, one positive and one negative. We are given the principal square root (9), so the other square root would be its negative (-9). To prove that, we square both numbers and we compare the results:
9 • 9 = 81
(-9). (-9)= 81
Question 2.
A square acre of land is 4,840 square yards. Between which two integers is the length of one side?
Options:
a. between 24 and 25 yards
b. between 69 and 70 yards
c. between 242 and 243 yards
d. between 695 and 696 yards
Answer:
b. between 69 and 70 yards
Explanation:
The area of a square is found by multiplying the side of the square by itself. Therefore, to Bud the side of the square, we have to take the square root of the area.
Let’s denote with A the area of the land and with each side of the square. We have:
A = 4840
A = s . s
A = s²
s = √A = √4840
Following the steps as in °Explore Activity on page 9, we can make an estimation for the irrational number:
4761 < 4840 < 4900
\(\sqrt { 4761 }\) < \(\sqrt { 4840 }\) < \(\sqrt { 4900 }\)
69 < \(\sqrt { 4840 }\) < 70
Each side of the land is between 69 and 70 yards.
Question 3.
Which of the following is an integer but not a whole number?
Options:
a. -9.6
b. -4
c. 0
d. 3.7
Answer:
b. -4
Explanation:
Whole numbers are not negative
-4 is an integer but not a whole number
Question 4.
Which statement is false?
Options:
a. No integers are irrational numbers.
b. All whole numbers are integers.
c. No real numbers are irrational numbers.
d. All integers greater than 0 are whole numbers.
Answer:
c. No real numbers are irrational numbers.
Explanation:
Rational and irrational numbers are real numbers.
Question 5.
Which set of numbers best describes the displayed weights on a digital scale that shows each weight to the nearest half pound?
Options:
a. whole numbers
b. rational numbers
c. real numbers
d. integers
Answer:
b. rational numbers
Explanation:
The scale weighs nearest to 1/2 pound.
Question 6.
Which of the following is not true?
Options:
a. π2 < 2π + 4
b. 3π > 9
c. \(\sqrt { 27 }\) + 3 > 172
d. 5 – \(\sqrt { 24 }\) < 1
Answer:
c. \(\sqrt { 27 }\) + 3 > 172
Explanation:
a. π2 < 2π + 4
(3.14)² < 2(3.14) + 4
9.86 < 10.28
True
b. 3π > 9
9.42 > 9
True
c. \(\sqrt { 27 }\) + 3 > 172
5.2 + 3 > 8.5
8.2 > 8.5
False
d. 5 – \(\sqrt { 24 }\) < 1
5 – 4.90 < 1
0.1 < 1
True
Question 7.
Which number is between \(\sqrt { 21 }\) and \(\frac{3π}{2}\) ?
Options:
a. \(\frac{14}{3}\)
b. 2 \(\sqrt { 6 }\)
c. 5
d. π + 1
Answer:
Explanation:
a. \(\sqrt { 21 }\) and \(\frac{3π}{2}\)
\(\sqrt { 21 }\) = 4.58
\(\frac{3π}{2}\) = 4.71
14/3 = 4.67
b. 2\(\sqrt { 6 }\) = 4.90
c. 5
d. π + 1 = 3.14 + 1 = 4.14
Question 8.
What number is shown on the graph?
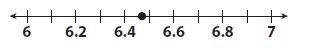
Options:
a. π+3
b. \(\sqrt { 4 }\) + 2.5
c. \(\sqrt { 20 }\) + 2
d. 6.\(\overline { 14 } \)
Answer:
c. \(\sqrt { 20 }\) + 2
Explanation:
6.48
a. π+3 = 3.14 + 3 = 6.14
b. \(\sqrt { 4 }\) + 2.5 = 2 + 2.5 = 4.5
c. \(\sqrt { 20 }\) + 2 = 4.47 + 2 = 6.47
d. 6.\(\overline { 14 } \) = 6.1414
Question 9.
Which is in order from least to greatest?
Options:
a. 3.3, \(\frac{10}{3}\), π, \(\frac{11}{4}\)
b. \(\frac{10}{3}\), 3.3, \(\frac{11}{4}\), π
c. π, \(\frac{10}{3}\), \(\frac{11}{4}\), 3.3
d. \(\frac{11}{4}\), π, 3.3, \(\frac{10}{3}\)
Answer:
d. \(\frac{11}{4}\), π, 3.3, \(\frac{10}{3}\)
Explanation:
10/3 = 3.3333333
11/4 = 2.75
![]()
Mini-Task
Question 10.
The volume of a cube is given by V = x3, where x is the length of an edge of the cube. The area of a square is given by A = x2, where x is the length of a side of the square. A given cube has a volume of 1728 cubic inches.
a. Find the length of an edge.
______ inches
Answer:
12 inches
Explanation:
V = x3
A = x2
1728 = x3
x = 12
The length of an edge = 12 in
Question 10.
b. Find the area of one side of the cube.
______ in2
Answer:
144 in2
Explanation:
A = (12)² = 144
Area of the side of the cube = 144 in2
Question 10.
c. Find the surface area of the cube.
______ in2
Answer:
864 in2
Explanation:
SA = 6 (12)² = 864
The surface area of the cube = 864 in2
Question 10.
d. What is the surface area in square feet?
______ ft2
Answer:
6 ft2
Explanation:
SA = 864/144 = 6
The surface area of the cube = 6 ft2
Conclusion:
If you are looking for the Grade 8 maths notes and textbook, then refer to Go Math Grade 8 Answer Key Chapter 1 Real Numbers. It is the best source for students to learn maths and get a good score in the exam.