Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Unit 2 Study Guide Review Answer Key.
Texas Go Math Grade 8 Unit 2 Study Guide Review Answer Key
Proportional Relationships
Essential Question
How can you use proportional relationships to solve real-world problems?
Exercises
Question 1.
The table represents a proportional relationship. Write an equation that describes the relationship. Then graph the relationship represented by the data. (Lessons 3.1,3.3, 3.4)
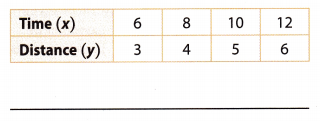
Answer:
slope = \(\frac{4-3}{8-6}\) = \(\frac{1}{2}\) = 0.5
Find the slope using given points by
Slope(m) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
where
(x2, y2) = (8, 4) and (x1, y1) = (6, 3)
y = 0.5x Substitute the slope m in the slope intercept form: y = mx + b.
Since the relationship is proportional, b = 0
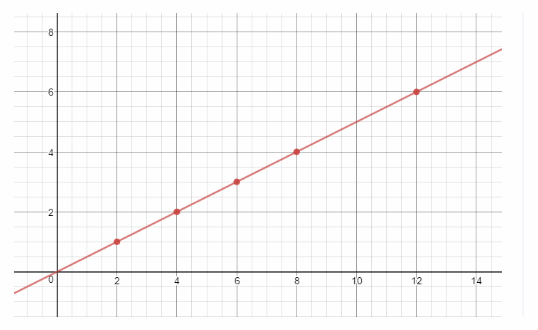
Graph the equation
Find the slope and the unit rate represented on each graph. (Lesson 3.2)
Question 2.
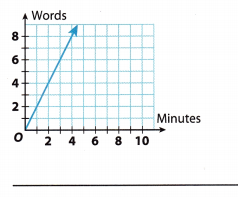
Answer:
Explanation A:
The slope formula is:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Substitute the values from the graph and find the value of slope (m).
m = \(\frac{4-0}{2-0}\)
m = \(\frac{4}{2}\)
m = 2
Explanation B:
Firstly, we will find the slope using following formula:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
We can calculate the slope using given formula on any two points located on a given function,
m = \(\frac{8-4}{4-2}\)
m = 2
Unit rate is defined as the comparison of two values where one of them is one unit. To simplify, in this exercise, unit rate would be the number of words in one minute, so we have to find a point on function where x value is 1. On given function, unit rate is 2 words per minute.
As it is shown in this exercise, unit rate and slope of the graph have the same value, but in a different format. Slope is an integer and unit rate is a rate of change of a mathematical function.
Question 3.
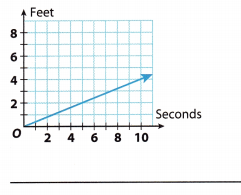
Answer:
Slope/unitrate = \(\frac{2-0}{5-0}\) = \(\frac{2}{5}\) = 0.4 Find the slope using given points by Slope(m) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) where (x2, y2) = (5, 2) and (x1, y1) = (0, 0)
The unit rate and the slope is
0.4 ft per sec
Module 4 Nonproportional Relationships
Essential Question
How can you use nonproportional relationships to solve real-world problems?
Exercises
Complete each table. Explain whether the relationship between x and y is proportional or nonproportional and whether it is linear. (Lesson 4.1)
Question 1.
y = 10x – 4
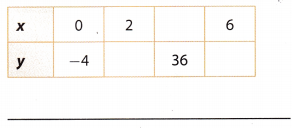
Answer:
y = 10x – 4 Given
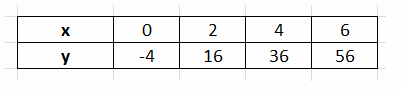
complete the table
Relationship is Linear but not proportional Compare with general linear equation: y = mx + b. Since, b ≠ 0, relationship is not proportional.
Question 2.
y = –\(\frac{3}{2} x\)
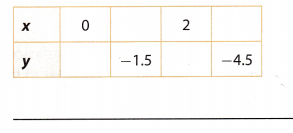
Answer:
Firstly, we will complete the given table by calculating the missing x and y values. To calculate the missing y values, we will multiply the corresponding x value with -1.5 and to get the missing x values we will divide the corresponding y value with -1.5.
Completed table is shown below.

Equation is linear if its graph is a straight line. Considering the fact that the graph of an equation y = \(\frac{3}{2} x\) is a straight line, we can claim that the relationship between x and y is linear.
To determine whether the given equation is proportional, we have to check two things. The first one is if ratios between x and y values are the same- Therefore:
–\(\frac{1}{1.5}\) = –\(\frac{2}{3.0}\) = –\(\frac{3}{4.5}\)
–\(\frac{2}{3} x\) = –\(\frac{2}{3}\) = –\(\frac{2}{3}\)
The other thing is if the graph goes through the origin. Considering the fact that point (0, 0) is shown in the table, we know that the graph goes through the origin.
Hence, we can conclude that given equation is proportional.
Question 3.
Find the slope and y-intercept for the linear relationship shown in the table. Graph the line. Is the relationship proportional or nonproportional? (Lessons 4.2,4.4)

slope ____
y-intercept ____
The relationship is ______
Answer:
Firstly, we will graph the equation using given x and y values from the table. Graph is shown in the picture below.
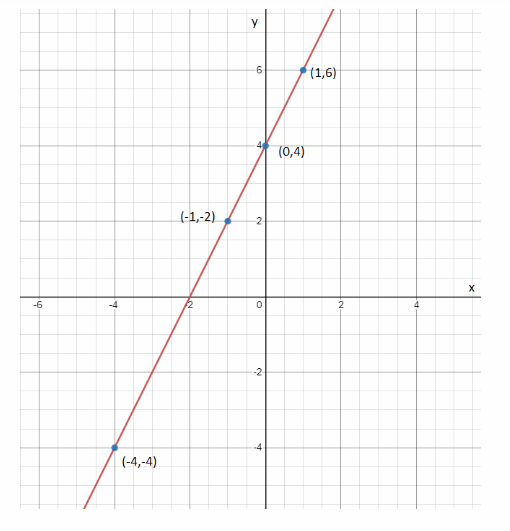
We can calculate the slope as following using any two points from the graph:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{4-2}{0-(-1)}\)
m = 2
y-intercept is defined as the value of y coordinate in a point where the function intersects with the y axis. Looking
at the graph, we can conclude that the line intersects with the y axis in point (0, 4).
Therefore, b = 4.
Having calculated the values of the slope and y-intercept, we can write the equation of a line:
y = mx + b
y = 2x + 1
Given relationship is not proportional considering the fact that the graph does not pass through the origin and noticing that the ratio between x and y values is not the same.
Question 4.
Tom’s Taxis charges a fixed rate of $4 per ride plus $0.50 per mile. Carla’s Cabs does not charge a fixed rate but charges $1.00 per mile. (Lessons 4.3, 4.5)
Answer:
Toms taxis charge a fixed rate of $4 per ride plus $0.50 per mile. Carlas Cabs does not charge a fixed rate but charges $ 1 .00 per tuile. To represent the cost of Toms Taxis and Carias cabs in equation, let us apply express
them using the slope—intercept form y = mx + b.
a. Write an equation that represents the cost of Tom’s Taxis. ______
Answer:
Representing the cost of Tom’s Taxis
Let y be the cost of Tom’s Taxis
x be the distance traveL by Tom’s Taxis (in mile)
m be the amount to be paid per mile
b be the amount to be paid per ride
Using y = mx + b, the representation of the cost of Tom’s Taxis where m = 0.50 and b = 4 is
y = 0.50x + 4
b. Write an equation that represents the cost of Carla’s cabs.
Answer:
Representing the cost of Carla’s cabs.
Let y be the cost of Carla’s cabs
x be the distance travel by Carla’s cabs (in mile)
m be the amount to be paid per mile
b be the amount to be paid per ride
Using y = mx + b, the representation of the cost of Carla’s cabs where m = 1 and b = 0 is
y = 1x + 0
y = x
c. Steve calculated that for the distance he needs to travel, Tom’s Taxis will charge the same amount as Carla’s Cabs. Graph both equations. How far is Steve going to travel and how much will he pay?
Answer:
To determine the distance Steve needs to travel that Tom’s Taxis will charge the same amount as Carla’s Cabs and
the amount he will pay, let us show the graph the two equations by setting the values of x and determine the corresponding values of y gives the following ordered pairs
For Tom’s Taxis y = 0.50x + 4

Plotting and connecting the points gives the graph of
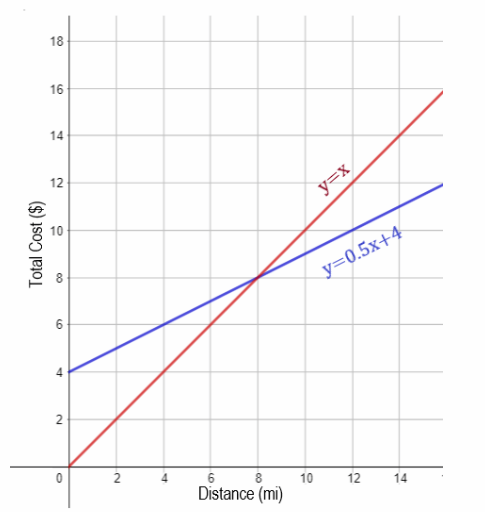
Now, looking at the graph, the the two lines intersect at (8, 8), meaning
Steve needs to travel 8 miles and he will pay an amount of $8.
See the explanation
Writing Linear Equations
Essential Question
How can you use linear equations to solve real-world problems?
Exercises
Question 1.
Ms. Thompson is grading math tests. She is giving everyone that took the test a 10-point bonus. Each correct answer is worth 5 points. Write an equation in slope-intercept that represents the scores on the tests. (Lesson 5.1) _______
The table shows a pay scale based on years of experience. (Lessons 5.1, 5.2)

Answer:
y = 5x + 10 Substitute m = 5 points and b = 10 point in scope-intercept form: y = mx + b. where x is the number of correct answers.
Question 2.
Find the slope for this relationship. ______
Answer:
Slope will be calculated using the fotbwing formula:
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\),
for any two points (x1, y1) and (x2, y2) on the graph.
Therefore, we can use formula from the previous step:
m = \(\frac{19-14}{4-2}\)
m = 2.5
Hence, the calculated slope for given relationship is:
m = 2.5
Question 3.
Find the y-intercept.
Answer:
9 = 2.5(0) + b Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b): y = mx + b
9 = 0 + b
b = 9
Question 4.
Write an equation in slope-intercept form that represents this relationship. ____
Answer:
y = 2.5x + 9
Substituting the value of slope (m) and y intercept(b) in slope intercept form: y = mx + b
Question 5.
Graph the equation, and use it to predict the hourly pay of someone with 10 years of experience.
Answer:
To graph the equation, we will find given points on the coordinate system and connect them to draw the graph.
In order to predict the hourly pay for someone with 10 years of experience, we will have to find a point on function where x = 10 and value of y coordinate in that points is the hourly pay as shown in the picture below.
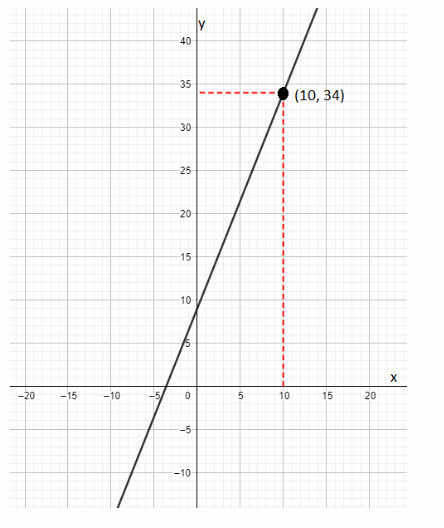
Hence, the hourly pay for someone with 10 years of experience is 34 dollars.
Does each of the following graphs represent a linear relationship? Why or why not? (Lesson 5.3)
Question 6.
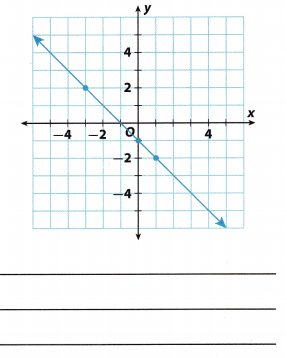
Answer:
To determine the answer here, we will review the definition of a linear function.
Equation is a linear function only if its graph is a straight line. Considering the fact that given graph is a straight line, we can conclude that the relationship is linear.
Question 7.
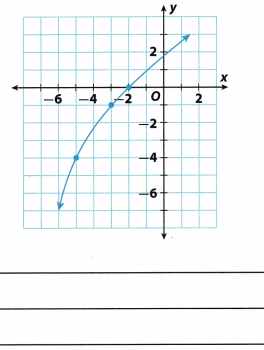
Answer:
Non-linear relationship Graph of a linear equation is a straight line
Functions
Essential Question
How can you use functions to solve real-world problems?
Exercises
Determine whether each relationship is a function. (Lesson 6.1)
Question 1.
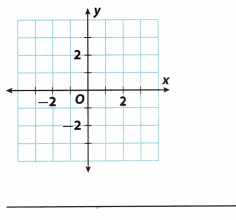
Answer:
Explanation A:
To determine the answer here, we will have to review on how to recognize a function.
A certain relationship represents a function only if each input value has one output value. To clarify, every X value
on the graph can have only one y value.
Considering the fact that in given graph there is no repetition of values, we can claim that the given relationship is a function.
Explanation B:
Based on the graph, it is a function since each input is paired with exactly one output
Question 2.
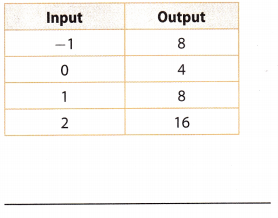
Answer:
Function Each input is paired with exactly one output
Tell whether the function is linear or nonlinear. (Lesson 6.2)
Question 3.
y = 5x + \(\frac{1}{2}\): ____
Answer:
y = 5x + \(\frac{1}{2}\) Compare with general linear equation: y = mx + b
Function is linear
Question 4.
y = x2 + 3 : ______
Answer:
y = x2 + 3 Compare with general linear equation: y = mx + b
Function is nonlinear
Question 5.
Elaine has a choice of two health club memberships. The first membership option is to pay $500 now and then pay $150 per month. The second option is shown in the table. Elaine plans to go to the club for 12 months. Which option is cheaper? Explain.
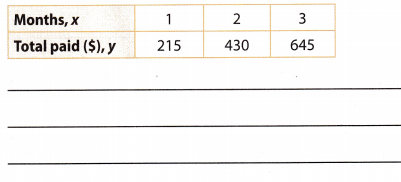
Answer:
To determine which is cheaper between Elaine’s two health club membership, where she plans to go for 12 months. Let us apply the slope-intercept form y = mx + b.
The first membership option is pay now $500 and then pay $150 per month.
Let us represent the following variables.
Let, y be the total membership fee for 12 months, m be the payment for every month, x be the number of months she plans to go the club, and b be the down Payment.
Now, to determine the total membership fee y for the first option, substitute the values of m = 150, x = 12, and
b = 500.
y = mx + b
y = 150(12) + 500
y = 1800 + 500
y = 2300
The total health club membership fee for the first option is
$2300
The second option is shown in the table below.
| Months. x|1 |2 |3 |
|—— |——| ——|———|
|Total paid($),y |215| 430| 645 |
Before we can find the total membership fee of the second option, Let us first determine the slope in using the first
two months of the payment plan, where x1 = 1, x2 = 2, y1 = 215, and y2 = 430
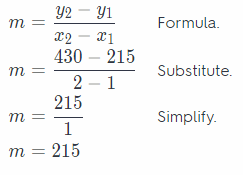
Next, Let us get the value of b, using x = 1 and y = 215, where m = 215.
y = mx + b Formula.
215 = 215(1) + b Substitute.
215 = 215 + b Simplify.
b = 215 – 215
b = 0
Now, to determine the total membership fee y for the second option, let us substitute the values of m = 215, x = 12, and b = 0.
y = mx + b
y = 215(12) + 0
y = 2580 + 0
y = 2580
The total health club membership fee for the second option is
$2580
Since the total health club membership fee for the first option $2300 is less than the total health club membership fee for the second option $2380, then
**the first option is cheaper that the second option**.
Texas Go Math Grade 8 Unit 2 Performance Tasks Answer Key
Question 1.
CAREERS IN MATH Cost Estimator To make MP3 players, a cost estimator determined it costs a company $1500 per week for overhead and $45 for each MP3 player made.
a. Define a variable to represent the number of players made. Then write an equation to represent the company’s total cost per week, c.
Answer:
Let n be the number of players made in a week Identify the variable
c = 45n + 1500 Company’s total cost
b. One week, the company spends $5460 making MP3 players. How many players were made that week? Show your work.
Answer:
c = 45n + 1500 Substitute c = $5460 in the equation
5460 = 45n + 1500
45n = 5460 – 1500
45n = 3960
n = \(\frac{3960}{45}\) = 88
The number of MP3 prayers made were 88
c. If the company sells MP3 players for $ 120, how much profit would it make if it sold 80 players in one week? Explain how you found your answer.
Answer:
c = 45n + 1500 Find the cost of making 80 players by substituting n = 80
c = 45(80) + 1500
c = $5100
r = 120 * 80 = $9600 each Find the revenue made by selling 80 players at $120 each
P = 9600 – 5100 = $4500 Profit = Cost – Revenue
Question 2.
A train from Portland, Oregon, to Los Angeles, California, travels at an average speed of 60 miles per hour and covers a distance of 963 miles. Susanna is taking the train from Portland to Los Angeles to see her aunt. She needs to arrive at her aunt’s house by 8 p.m. It takes 30 minutes to get from the train station to her aunt’s house.
a. By what time does the train need to leave Portland for Susanna to arrive by 8 p.m.? Explain how you got your answer. As part of your explanation, write a function that you used in your work.
Answer:
Given that, a train traveling from Portland, Oregon to Los Angeles, California travels at an average speed of
60 miles per hour and covers a distance of 963 miles.
Time = Distance/Speed
Time = 963/60
Time = 16.05 hours
Subtract 16.05 hours from 8.00 P.M.
8 – 16.05 hours = 4.55 A.M
b. Susanna does not want to leave Portland later than 10 p.m. or earlier than 6 a.m. Does the train in part a meet her requirements? If not, give a new departure time that would allow her to still get to her aunt’s house on time, and find the arrival time of that train.
Answer:
Susanna is traveling to her aunt’s house from Portland to Los Angeles. It will take 30 min to get from the station to her aunt’s house and she needs to arrive aunt’s house by 8 pm.
The departure time of the train should be 4.55 am to meet her requirements.
Susanna does not want to leave Portland later than 10 pm or earlier than 6 am. The arrival time of the train will be 9 pm.
Texas Go Math Grade 8 Unit 2 Mixed Review Texas Test Prep Answer Key
Selected Response
Question 1.
Rickie earns $7 an hour babysitting. Which table represents this proportional relationship?
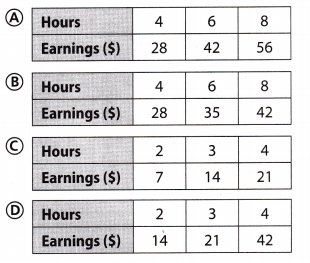
Answer:
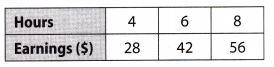
Explanation:
y = 7x where y represents the total earning and x represents the number of hour
y = 7(4) = 28 Substitute x = 4, 6, 8
y = 7(6) = 42
y = 7(8) = 56
Option A represents this proportional relationship
Question 2.
Which of the relationships function?
(A) (6, 3), (5, 2), (6, 8), (0, 7)
(B) (8, 2), (1, 7), (-1, 2), (1, 9)
(C) (4, 3), (3, 0), (-1, 3), (2, 7)
(D) (7, 1), (0, 0), (6, 2), (0, 4)
Answer:
(C) (4, 3), (3, 0), (-1, 3), (2, 7)
Explanation:
Each input has exactly one output. In other options, there is an input paired with more than one output
Question 3.
Which set best describes the numbers used on the scale for a standard thermometer?
(A) whole numbers
(B) rational numbers
(C) real numbers
(D) integers
Answer:
(B) rational numbers
Explanation:
The standard thermometer is measured nearest to 0.1 degree
Question 4.
Which term refers to slope?
(A) rate of change
(B) equation
(C) y-intercept
(D) coordinate
Answer:
(A) rate of change
Explanation:
Rate of change
Slope and rate of change gives the change in second quantity as compared to unit of first quantity.
Question 5.
The graph of which equation is shown below?
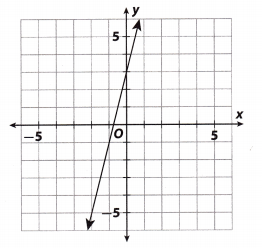
(A) y = 4x + 3
(B) y = -4x – 0.75
(C) y = -4x + 3
(D) y = 4x – 0.75
Answer:
(A) y = 4x + 3
Explanation:
Option B and D are rejected. The graph has a y intercept of 3
Option C is rejected The slope of the graph would be positive (as the graph rises from left to right)
Hence, the equation of the garph is y = 4x + 3
Option A
Question 6.
Which equation represents a nonproportional relationship?
(A) y = 5x
(B) y = -5x
(C) y = 5x + 3
(D) y = –\(\frac{1}{5} x\)
Answer:
(C) y = 5x + 3
Explanation:
y = 5x + 3 Comparing with linear equation: y = mx + b. Since b ≠ 0, the equation is non proportional represents a non-proportional relationship
Question 7.
Which describes the solution of a system of linear equations for two lines with the same slope and the same y-intercepts?
(A) one nonzero solution
(B) infinitely many solutions
(C) no solution
(D) solution of 0
Answer:
(B) infinitely many solutions
Question 8.
Which is 7.0362 × 10-4 written in standard notation?
(A) 0.000070362
(B) 0.00070362
(C) 7.0362
(D) 7036.2
Answer:
(B) 0.00070362
Explanation:
7.0362 × 10-4 Given
4 use me exponent the power of 10 to see how many places to move the decimal point.
places
0.00070362 Place the decimal point. Since you are going to write a number less than 7.0362, move the decimal to the left Add placeholder zeros if necessary.
Question 9.
Which term does not correctly describe the function shown in the table?
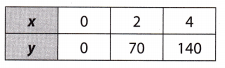
(A) relationship
(B) linear
(C) proportional
(D) nonproportional
Answer:
(D) nonproportional
Explanation:
Non proportional The relationship is a function as each input has exactly one output. It is linear as rate of change is constant. It is proportional as table contain (0, 0). Hence, a relationship that is proportional cannot be non
proportional.
Question 10.
As part of a science experiment, Greta measured the amount of water flowing from Container A to Container B. Container B had half a gallon of water in it to start the experiment. Greta found that the water was flowing at a rate of two gallons per hour. Which equation represents the amount of water in Container B?
(A) y = 2x
(B) y = 0.5x
(C) y = 2x + 0.5
(D) y = 0.5x + 2
Answer:
(C) y = 2x + 0.5
Explanation:
y = 2x + 0.5
where y is the number of gallons after x hours. The slope or rate of change is 2 gallons per hr and the initial number of gallons in Container B (y intercept).
Use the slope intercept form: y = mx + b
Gridded Response
Question 11.
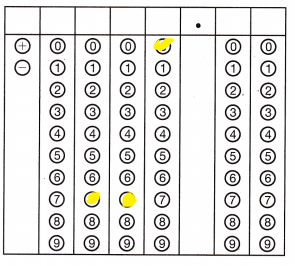
A factory produces gaskets at a constant rate. After 6 hours, 4620 gaskets have been produced. How many gaskets does the factory produce per hour?
Answer:
Given that,
The factory produces gaskets at a constant rate.
After 6 hours there are 4620 gaskets.
Per 1 hour = 4620/6 = 770
The gaskets per 1 hour = 770
Question 12.
The table below represents a linear relationship.
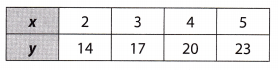
What is the y-intercept?
Answer:
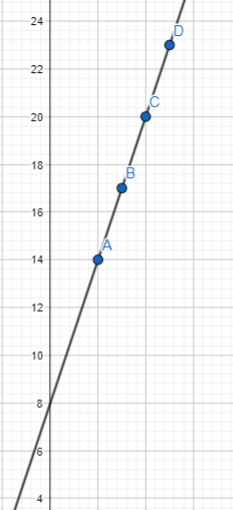
The Y-intercept is (0,8)
Hot Tip!
Estimate your answer before solving the question. Use your estimate to check the reasonableness of your answer.
Question 13.
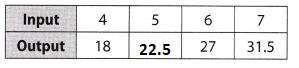
The table below shows some input and output values of a function.
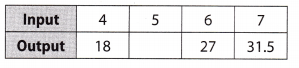
What number is missing?
Answer:
31.5 – 27 = 4.5
18+4.5 = 22.5
Texas Go Math Grade 8 Unit 2 Vocabulary Preview Answer Key
Use the puzzle to preview key vocabulary from this unit. Unscramble the circled letters within the found words to answer the riddle at the bottom of the page.

- The y-coordinate of the point where the graph crosses the y-axis. (Lesson 4-2)
- A rule that assigns exactly one output to each input. (Lesson 6-1)
- The result after applying the function machines rule. (Lesson 6-1)
- A relationship written as y = kx, where the data increases or decreases together at a constant rate (2 words). (Lesson 3-4)
- The ratio of change in rise to the corresponding change in run on a graph. (Lesson 3-2)
- A set of data that is made up of two paired variables. (Lesson 5-3)
- An equation whose solutions form a straight line on a coordinate plane. (Lesson 4-1)
Question.
How much of the money earned does a professional sports team pay its star athlete?
Answer:
An ____ ____ ____ ____ ____ ____ – ____ ____ ____ ____ ____ ____ ____!