Texas Go Math Grade 8 Module 8 Answer Key The Pythagorean Theorem

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 8 Answer Key The Pythagorean Theorem.

Texas Go Math Grade 8 Module 8 Answer Key The Pythagorean Theorem

Texas Go Math Grade 8 Module 8 Are You Ready? Answer Key

Find the square of each number.

Question 1.
5 _________
Answer:
To determine the square of a number x, denoted by x² just multiply the given number x by itself.
Now, let us get the square of 5 or the equivalent of 5², just multiply 5 by itself, that is
5² = 5 × 5
= 25
or

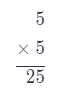
Question 2.
16 __________
Answer:
When solving for the square of a number, we need to multiply the certain number by itself.
To find the square of 16, we simply multiply it by itself
16² = 16 × 16
= 256

Question 3.
-11 _________
Answer:
To determine the square of a number x, denoted by x² just multiply the given number x by itself.
Now, let us get the square of -11 or the equivalent of (-11)², just multiply 11 by itself, that is
(-11)² = -11(-11)
= 121

Question 4.
\(\frac{2}{7}\) __________
Answer:
To solve for the square of \(\frac{2}{7}\), we simply multiply it by itself. Take note that in multiplying fractions, the product is equal to the product of all numerators divided by the product of all denominators.
(\(\frac{2}{7}\))² = \(\frac{2}{7}\) × \(\frac{2}{7}\) = \(\frac{4}{49}\)

Evaluate each expression.

Question 5.
\(\sqrt{(6+2)^{2}+(3+3)^{2}}\) __________
Answer:
\(\sqrt{(6+2)^{2}+(3+3)^{2}}=\sqrt{8^{2}+6^{2}}\) (First, operate within parentheses.) …… (1)
= \(\sqrt{64+36}\) (Next, simplify exponents.) ………. (2)
= \(\sqrt{100}\) (Then add and subtract left to right.) ……….. (3)
= 10 (Finally, take the square root.) ……… (4)
= 10

Question 6.
\(\sqrt{(9-4)^{2}+(5+7)^{2}}\) __________
Answer:
\(\sqrt{(9-4)^{2}+(5+7)^{2}}=\sqrt{5^{2}+12^{2}}\) (First, operate within parentheses.) …… (1)
= \(\sqrt{25+144}\) (Next, simplify exponents.) ………. (2)
= \(\sqrt{169}\) (Then add and subtract left to right.) ……….. (3)
= 13 (Finally, take the square root.) ……… (4)
= 13

Question 7.
\(\sqrt{(10-6)^{2}+(15-12)^{2}}\) __________
Answer:
\(\sqrt{(10-6)^{2}+(15-12)^{2}}=\sqrt{4^{2}+3^{2}}\) (First, operate within parentheses.) …… (1)
= \(\sqrt{16+9}\) (Next, simplify exponents.) ………. (2)
= \(\sqrt{25}\) (Then add and subtract left to right.) ……….. (3)
= 5 (Finally, take the square root.) ……… (4)
= 5

Question 8.
\(\sqrt{(6+9)^{2}+(10-2)^{2}}\) __________
Answer:
\(\sqrt{(6+9)^{2}+(10-2)^{2}}=\sqrt{15^{2}+8^{2}}\) (First, operate within parentheses.) …… (1)
= \(\sqrt{225+64}\) (Next, simplify exponents.) ………. (2)
= \(\sqrt{289}\) (Then add and subtract left to right.) ……….. (3)
= 17 (Finally, take the square root.) ……… (4)
= 17

Simplify each expression.

Question 9.
5(8)(10) ___________
Answer:
5(8)(10) = (40)(10) (Multiply from left to right)
= 400

Question 10.
\(\frac{1}{2}\)(6)(12) ___________
Answer:
\(\frac{1}{2}\)(6)(12) = (3)(12) (Multiply from left to right)
= 36

Question 11.
\(\frac{1}{3}\)(3)(12) ___________
Answer:
\(\frac{1}{3}\)(3)(12) = (1)(12) (Multiply from left to right)
= 12

Question 12.
\(\frac{1}{2}\)(8²)(4) ___________
Answer:
Simplify expression
\(\frac{1}{2}\)(8²)(4) = \(\frac{1}{2}\)(64)(4) (Simplify the exponent) …………. (1)
= (32)(4) (Multiply from left to right) ……………… (2)
= 128

Question 13.
\(\frac{1}{4}\)(10)²(15) ___________
Answer:
Simplify expression
\(\frac{1}{4}\)(10²)(15) = \(\frac{1}{4}\)(100)(15) (Simplify the exponent) …………. (1)
= (25)(15) (Multiply from left to right) ……………… (2)
= 375

Question 14.
\(\frac{1}{3}\)(9)²(6) ___________
Answer:
Simplify expression
\(\frac{1}{3}\)(9²)(6) = \(\frac{1}{3}\)(81)(6) (Simplify the exponent) …………. (1)
= (27)(6) (Multiply from left to right) ……………… (2)
= 162

Texas Go Math Grade 8 Module 8 Reading Start-Up Answer Key

Visualize Vocabulary

Use the ✓ words to complete the graphic.

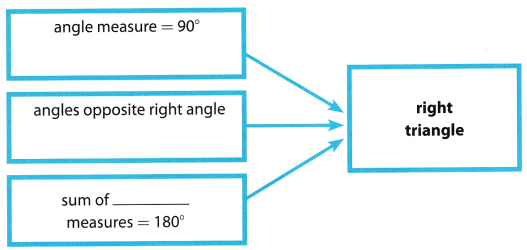
Understand Vocabulary

Match the term on the left to the correct expression on the right.

Answer:
1 – C. Hypotenuse: The side opposite the right angle in a right triangle
2 – A. Theorem: An idea that has been demonstrated as true.
3 – B. Legs: The two sides that form the right angle of a right triangle.

Active Reading
Booklet Before beginning the module, create a booklet to help you learn about the Pythagorean Theorem. Write the main idea of each lesson on each page of the booklet. As you study each lesson, write important details that support the main idea, such as vocabulary and formulas. Refer to your finished booklet as you work on assignments and study for tests.