Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 3 Answer Key Proportional Relationships.
Texas Go Math Grade 8 Module 3 Answer Key Proportional Relationships

Essential Question
How can you use proportional relationships to solve real-world problems?
Texas Go Math Grade 8 Module 3 Are You Ready? Answer Key
Complete these exercises to review skills you will need for this chapter.
Write each fraction as decimal.
Question 1.
\(\frac{3}{8}\)
Answer:
To express \(\frac{3}{8}\) as a decimal, we write the fraction as a division problem.

Therefore, \(\frac{3}{8}\) = 0.375
Question 2.
\(\frac{0.3}{0.4}\)
Answer:
First, multiply the numerator and the denominator by 10 so that the denominator is a whole number.
\(\frac{0.3 \times 10}{0.4 \times 10}\) = \(\frac{3}{4}\)
Now write the fraction as a division problem, place a decimal point in the quotient and divide as whole numbers:
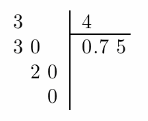
0.75
Question 3.
\(\frac{0.13}{0.2}\)
Answer:
First multiply the numerator and the denominator by 10 so that the denominator is a whole number.
\(\frac{0.13 \times 10}{0.2 \times 10}\) = \(\frac{1.3}{2}\)
Now write the fraction as a division problem. place a decimal point in the quotient and divide as whole numbers:
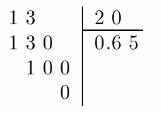
0.65
Question 4.
\(\frac{0.39}{0.75}\)
Answer:
First, multiply the numerator and the denominator by 100 so that the denominator is a whole number.
\(\frac{0.39 \times 100}{0.75 \times 100}\) = \(\frac{39}{75}\)
Now write the fraction as a division problem, place a decimal point in the quotient and divide as whole numbers:
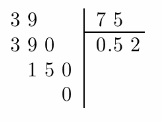
0.52
Question 5.
\(\frac{4}{5}\)
Answer:
Write the fraction as a division problem, place a decimal point in the quotient and divide as whole numbers
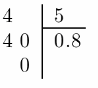
\(\frac{4}{5}\) = 0.8
Question 6.
\(\frac{0.1}{2}\)
Answer:
First, we multiply the numerator and the denominator by a power of 10 so that we get whole numbers.
\(\frac{0.1}{2}\) = \(\frac{0.1 \cdot 10}{2 \cdot 10}\) = \(\frac{1}{20}\)
To express \(\frac{1}{20}\) as a decimal, we write the fraction as a division problem.
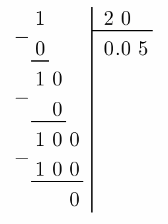
Therefore,
\(\frac{0.1}{2}\) = 0.05
Question 7.
\(\frac{3.5}{14}\)
Answer:
First, we multiply the numerator and the denominator by a power of 10 so that we get whole numbers.
\(\frac{3.5}{14}\) = \(\frac{3.5 \cdot 10}{14 \cdot 10}\) = \(\frac{35}{140}\)
To express \(\frac{35}{140}\) as a decimal, we write the fraction as a division problem.

Therefore, \(\frac{3.5}{14}\) = 0.25
Question 8.
\(\frac{7}{14}\)
Answer:
To express \(\frac{7}{14}\) as a decimal, we write the fraction as a division problem.
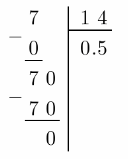
\(\frac{7}{14}\) = 0.5
Question 9.
\(\frac{0.3}{10}\)
Answer:
First, we multiply the numerator and the denominator by a power of 10 so that we get whole numbers.
\(\frac{0.3}{10}\) = \(\frac{0.3 \cdot 10}{10 \cdot 10}\) = \(\frac{3}{100}\)
To express \(\frac{3}{100}\) as a decimal, we write the fraction as a division problem.
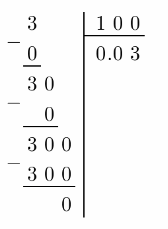
\(\frac{0.3}{10}\) = 0.03
Solve each proportion for x.
Question 10.
\(\frac{20}{18}\) = \(\frac{10}{x}\) ______
Answer:
\(\frac{20}{18}\) = \(\frac{10}{x}\) Given
\(\frac{20 \div 2}{18 \div 2}\) = \(\frac{10}{x}\) Divide 20 ÷ 2 = 10, so divide the numerator and denominator by 2
\(\frac{10}{9}\) = \(\frac{10}{x}\)
x = 9 compare
Question 11.
\(\frac{x}{12}\) = \(\frac{30}{72}\) ______
Answer:
\(\frac{x}{12}\) = \(\frac{30}{72}\) Given
\(\frac{x}{12}\) = \(\frac{30 \div 6}{72 \div 6}\) Divide 72 ÷ 6 = 12, so divide the numerator and denominator by 6.
\(\frac{x}{12}\) = \(\frac{5}{12}\)
x = 5 compare
Question 12.
\(\frac{x}{4}\) = \(\frac{4}{16}\) ______
Answer:
\(\frac{x}{4}\) = \(\frac{4}{16}\) Given
\(\frac{x}{4}\) = \(\frac{4 \div 4}{16 \div 4}\) Divide 16 ÷ 4 = 4, so divide the numerator and denominator by 4.
\(\frac{x}{4}\) = \(\frac{1}{4}\)
x = 1 compare
Question 13.
\(\frac{11}{x}\) = \(\frac{132}{120}\) ______
Answer:
\(\frac{11}{x}\) = \(\frac{132}{120}\) Given
\(\frac{11}{x}\) = \(\frac{132 \div 12}{120 \div 12}\) Divide 132 ÷ 12 = 11, so divide the numerator and denominator by 12.
\(\frac{11}{x}\) = \(\frac{11}{10}\)
x = 10 compare
Question 14.
\(\frac{36}{48}\) = \(\frac{x}{4}\) ______
Answer:
\(\frac{36}{48}\) = \(\frac{x}{4}\) Given
\(\frac{36 \div 12}{48 \div 12}\) = \(\frac{x}{4}\) Divide 48 ÷ 12 = 4, so divide the numerator and denominator by 12.
\(\frac{3}{4}\) = \(\frac{x}{4}\)
x = 3 compare
Question 15.
\(\frac{x}{9}\) = \(\frac{21}{27}\) ______
Answer:
\(\frac{x}{9}\) = \(\frac{21}{27}\) Given
\(\frac{x}{9}\) = \(\frac{21 \div 3}{27 \div 3}\) Divide 27 ÷ 3 = 9, so divide the numerator and denominator by 12.
\(\frac{x}{9}\) = \(\frac{7}{9}\)
x = 7 Compare
x = 7
Question 16.
\(\frac{24}{16}\) = \(\frac{x}{2}\) ______
Answer:
\(\frac{24}{16}\) = \(\frac{x}{2}\) Given
\(\frac{24 \div 8}{16 \div 8}\) = \(\frac{x}{2}\) Divide 16 ÷ 8 = 2, so divide the numerator and denominator by 8.
\(\frac{3}{2}\) = \(\frac{x}{2}\)
x = 3 Compare
x = 3
Question 17.
\(\frac{30}{15}\) = \(\frac{6}{x}\) ______
Answer:
\(\frac{30}{15}\) = \(\frac{6}{x}\) Given
\(\frac{30 \div 5}{15 \div 5}\) = \(\frac{6}{x}\) Divide 30 ÷ 5 = 6, so divide the numerator and denominator by 5.
\(\frac{6}{3}\) = \(\frac{6}{x}\)
x = 3 Compare
x = 3
Question 18.
\(\frac{3}{x}\) = \(\frac{18}{36}\) ______
Answer:
\(\frac{3}{x}\) = \(\frac{18}{36}\)
\(\frac{3}{x}\) = \(\frac{18 \div 6}{36 \div 6}\) Divide 18 ÷ 6 = 3, so divide the numerator and denominator by 6.
\(\frac{3}{x}\) = \(\frac{3}{6}\)
x = 6
Texas Go Math Grade 8 Module 3 Reading Start-Up Answer Key
Visualize Vocabulary
Use the ✓ words to complete the diagram.
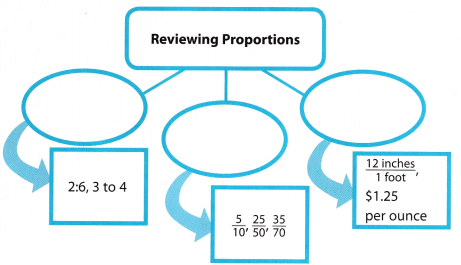
Understand Vocabulary
Match the term on the left to the definition on the right.

Answer:
1. (B) A unit rate is: B. A rate in which the second quantity in the comparison is one unit.
2. (A) Constant of proportionality is: A. A constant ratio of two variables related proportionally.
3. (C) A proportional relationship is: C. A relationship between two quantities in which the ration of one quantity to the other quantity is constant.