Texas Go Math Grade 8 Module 15 Quiz Answer Key

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 15 Quiz Answer Key.

Texas Go Math Grade 8 Module 15 Quiz Answer Key

Texas Go Math Grade 8 Module 15 Ready to Go On? Answer Key

15.1 Mean Absolute Deviation

The table shows scores for a gymnastics team. Use the table for 1-3.

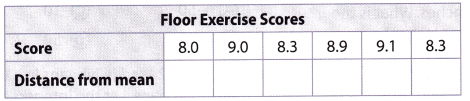
Question 1.
Find the mean of the scores. ___________________________
Answer:
Given that,
The scores are 8.0, 9.0, 8.3, 8.9, 9.1, 8.3.
Sum of scores = 51.6
The formula for the mean = sum of the scores/number of the scores.
Mean of scores = 51.6/6 = 8.6.

Question 2.
Complete the table to find the distance of each score from the mean.
Answer:

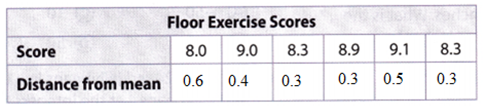
The formula for the mean of distance = Mean of scores – each value of the mean.
Ignore the signs.
8.6 – 8.0 = 0.6
8.6 – 9.0 = 0.4
8.6 – 8.3 = 0.3
8.6 – 8.9 = 0.3
8.6 – 9.1 = 0.5
8.6 – 8.3 = 0.3

Question 3.
Find the mean absolute deviation. _____________________________
Answer:
Mean of scores = 51.6/6 = 8.6.
Absolute value = Mean – each scores
Ignore the signs.
8.6 – 8.0 = 0.6
8.6 – 9.0 = 0.4
8.6 – 8.3 = 0.3
8.6 – 8.9 = 0.3
8.6 – 9.1 = 0.5
8.6 – 8.3 = 0.3
Mean absolute deviation = sum of absolute values – number of absolute values.
= 0.6 + 0.4 + 0.3 + 0.3 + 0.5 + 0.3/6 = 2.4/6 = 0.4
Mean absolute deviation = 0.4

15.2 Generating Random Samples

A manufacturer ships a store 5000 MP3 players, of which 300 are defective. The store manager does not know this but tests a random sample of 10 players to look for problems. A graphing calculator is used to simulate the sample, with 1-300 representing the defective players. The results are shown in the table.

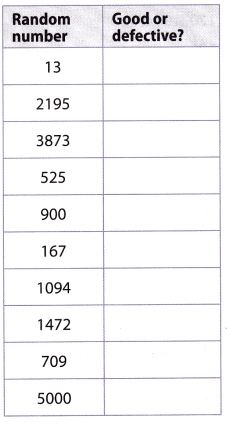
Question 4.
Complete the table to tell whether each number generated represents a good or defective player.
Answer:
Given that,
A manufacturer ships a store = 5000 MP3 players
Of that 300 are defective players.
He randomly checks the 10 players.
1-300 representing the defective players.

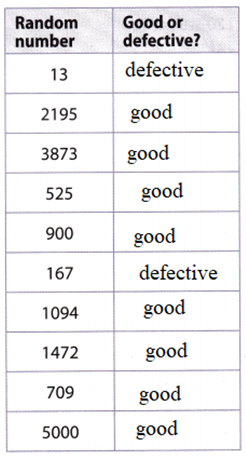
Question 5.
From this sample, how many defective players might the manager expect?
Answer: The manager expects 2 defective players as per the information seen in the above table.

Question 6.
Is the manager’s expectation accurate? Explain.
Answer:

Essential Question

Question 7.
How can you use random samples to solve real-world problems?
Answer:
Yes, you use random samples to solve real-world problemsRandom samples are a technique used to select the items or people. For this, you can use random sampling. For example, you have 10 papers and you have to divide them into different groups using random samples.

Texas Go Math Grade 8 Module 15 Mixed Review Texas Test Prep Answer Key

Selected Response

Question 1.
The radius of a ball is 4 inches. What is the volume of the ball in cubic inches?
(A) 16π in³
(B) \(\frac{64 \pi}{3}\) in³
(C) \(\frac{256 \pi}{3}\) in³
(D) \(\frac{4096 \pi}{3}\) in³
Answer:
Given that radius of the ball = 4 inches.
Volume of the ball = 4/3πr³
= 4/3(π×(4)³
= 4/3(π × 64)
= \(\frac{256 \pi}{3}\) in³
Option C is the correct answer.

Question 2.
A random sample of 30 students were asked to pick their favorite school subject, and 12 of them answered math. There are 480 students in the school. How many students in the school are likely to pick math as their favorite subject?
(A) 120 students
(B) 192 students
(C) 288 students
(D) 360 students
Answer:
Given,
A random sample of 30 students was asked to pick their favorite school subject, and 12 of them answered math.
There are 480 students in the school.
(480 ÷ 30) × 12 = 192 students
Thus 192 students in the school are likely to pick math as their favorite subject.

Question 3.
For which situation could flipping a coin be used to simulate a random sample?
(A) to predict the number of defective cell phones in a shipment of 2000 phones
(B) to predict the number of days in a month it will rain
(C) to predict the number of blue marbles in a box of 200 marbles
(D) to predict the number of boys or girls born at a hospital in a year
Answer:
Flipping a coin be used to simulate a random sample for the situation to predict the number of defective cell phones in a shipment of 2000 phones
Option A is the correct answer.

Question 4.
Vertex A of triangle ABC is located at the point (2, 5). Which transformation moves vertex A to the point (-2, 5)?
(A) reflection across the x-axis
(B) reflection across they-axis
(C) (x, y) → (x + 4, y)
(D) (x, y) → (x – 4, -y)
Answer:
(2,5) is in the first quadrant.
(-2,5) is in the second quadrant.
Translation transformation moves vertex A to the point (-2, 5).
The reflection is across the y axis.

Question 5.
Which number is closest to \(\sqrt {111}\)?
(A) -50
(B) -10
(C) 10
(D) 50
Answer:
\(\sqrt {111}\) = square root(111) = 10
Option C is the correct answer.

Question 6.
There are 24 red jellybeans in a bag of 140 jellybeans. Let the integers 1-24 represent the red jellybeans in a calculator simulation of the situation that generates random integers from 1 to 140. A sample of 15 “jellybeans” gives the following:

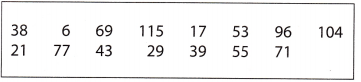
Using the sample, which is the best prediction of the number of jelly beans in the bag?
(A) 5
(B) 24
(C) 28
(D) 55
Answer:

Gridded Response

Question 7.
The table below shows the height in meters of several buildings. What is the mean absolute deviation of the data set?

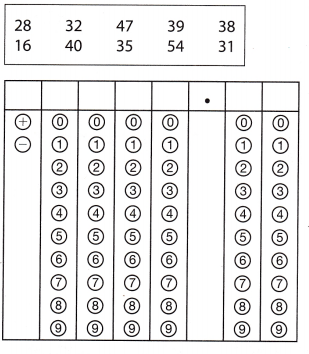
Answer:
Given data is 28, 32, 47, 39, 38, 16, 40, 35, 54, 31.
Mean = sum of the heights/number of the heights = 360/10 = 36.
Absolute value =mean – each of the heights.
36 – 28 = 8
36 – 32 = 4
36 – 47 = 11
36 – 39 = 3
36 – 16 = 20
36 – 40 = 4.
36 – 35 = 1
36 – 54 = 18
36 – 31 = 5
Mean absolute deviation = sum of absolute values – number of absolute values
= 74/9 = 65.
Mean absolute deviation = 65.