Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 8.2 Answer Key Converse of the Pythagorean Theorem.
Texas Go Math Grade 8 Lesson 8.2 Answer Key Converse of the Pythagorean Theorem
Texas Go Math Grade 8 Lesson 8.2 Explore Activity Answer Key
Testing the Converse of the Pythagorean Theorem
The Pythagorean Theorem states that if a triangle is a right triangle, then a2 + b2 = c2.
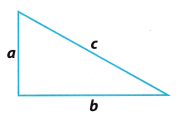
The converse of the Pythagorean Theorem states that if a2 + b2 = c2, then the triangle is a right triangle.
Decide whether the converse of the Pythagorean Theorem is true.
A. Verify that the following sets of lengths make the equation a2 + b2 = c2 true. Record your results in the table.

B. For each set of lengths in the table, cut strips of grid paper with a width of one square and lengths that correspond to the values of a, b, and c.
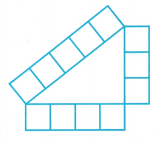
C. For each set of lengths, use the strips of grid paper to try to form a right triangle. An example using the first set of lengths is shown. Record your findings in the table.
Reflect
Question 1.
Draw Conclusions Based on your observations, explain whether you think the converse of the Pythagorean Theorem is true.
Answer:
Based on our observations, we saw that the sets of lengths that made the equation a2 + b2 = c2 true, also formed a right triangle. Therefore, the converse of the Pythagorean Theorem is true.
Example 1
Tell whether each triangle with the given side lengths is a right triangle.
A. 9 inches, 40 inches, and 41 inches
Let a = 9, b = 40, and c = 41.

Since 92 + 402 = 412, the triangle is a right triangle by the converse of the Pythagorean Theorem.
B. 8 meters, 10 meters, and 12 meters
Let a = 8, b = 10, and c = 12.

Since 82 + 102 ≠ 122, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Your Turn
Tell whether each triangle with the given side lengths is a right triangle.
Question 2.
14 cm, 23 cm, and 25 cm
Answer:
The converse of the Pythagorean Theorem gives you a way to tell if a triangle is a right triangle when you know the side lengths. The Longest side is 25cm, so thats the hypothenuse c. Let a = 14cm and b = 23cm.
a2 + b2 = c2 …………. (1)
142 + 232 = 252 (Substitute into the formula) ………….. (2)
196 + 529 = 625 (Simplify) ………… (3)
725 ≠ 625 (Add) ……….. (4)
Since 142 + 232 ≠ 252, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Question 3.
16 in., 30 in., and 34 in.
Answer:
The converse of the Pythagorean Theorem gives you a way to tell if a triangle is a right triangle when you know the side lengths. The longest side is 34 in, so thats the hypothenuse c = 34 in. Let a = 30 in and b = 16 in.
a2 + b2 = c2 …………. (1)
302 + 162 = 342 (Substitute into the formula) ………….. (2)
900 + 256 = 1156 (Simplify) ………… (3)
1156 = 1156 (Add) ……….. (4)
Since 302 + 162 = 342, the triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 4.
27 ft, 36 ft, 45 ft
Answer:
The converse of the Pythagorean Theorem gives you a way to tell if a triangle is a right triangle when you know the side lengths. The longest side is the hypothenuse c = 45 cm. Let a = 27 cm and b = 36 cm.
a2 + b2 = c2 …………. (1)
272 + 362 = 452 (Substitute into the formula) ………….. (2)
729 + 1296 = 2025 (Simplify) ………… (3)
2025 = 2025 (Add) ……….. (4)
Since 272 + 362 = 452, the triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 5.
11 mm, 18 mm, 21 mm
Answer:
The converse of the Pythagorean Theorem gives you a way to tell if a triangle is a right triangle when you know the side lengths. Let a = 11 mm, b = 18 m and C = 2 1 mm.
a2 + b2 = c2 …………. (1)
112 + 182 = 212 (Substitute into the formula) …………. (2)
121 + 324 = 441 (Simplify) ………… (3)
445 ≠ 441 (Add) ………………… (4)
Since 112 + 182 ≠ 212, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Example 2
Katya is buying edging for a triangular flower garden she plans to build in her backyard. If the lengths of the three pieces of edging that she purchases are 13 feet, 10 feet, and 7 feet, will the flower garden be in the shape of a right triangle?
Use the converse of the Pythagorean Theorem. Remember to use the longest length for c.
Let a = 7, b = 10,and c = 13.
a2 + b2 = c2

Since 72 + 102 ≠ 132, the garden will not be in the shape of a right triangle.
Your Turn
Question 6.
A blueprint for a new triangular playground shows that the sides measure 480 ft, 140 ft, and 500 ft. Is the playground in the shape of a right triangle? Explain.
Answer:
Let a = 480 ft, b = 140 ft and c = 500 ft
a2 + b2 = c2 …………. (1)
4802 + 1402 = 5002 (Substitute into the formula) ………… (2)
230400 + 19600 = 250000 (Simplify) ………… (3)
250000 = 250000 (Add) ………….. (4)
Since 4802 + 1402 = 5002 the playground is in the shape of a right triangle.
Question 7.
A triangular piece of glass has sides that measure 18 in., 19 in., and 25 in. Is the piece of glass in the shape of a right triangle? Explain.
Answer:
Let a = 18 in, b = 19 in and c = 25 in
a2 + b2 = c2 …………. (1)
182 + 192 = 252 (Substitute into the formula) ………… (2)
324 + 361 = 625 (Simplify) ……………. (3)
685 ≠ 625 (Add) …………… (4)
Since 182 + 192 ≠ 252, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
The piece of glass is not in the shape of a right triangle.
Question 8.
A corner of a fenced yard forms a right angle. Can you place a 12 foot long board across the corner to form a right triangle for which the leg lengths are whole numbers? Explain.
Answer:
No, we cannot find two whole numbers to serve as leg lengths, such that the sum of their squares to be 144.
Texas Go Math Grade 8 Lesson 8.2 Guided Practice Answer Key
Question 1.
Lashandra used grid paper to construct the triangle shown. (Explore Activity)
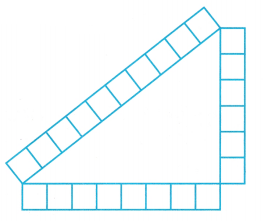
a. What are the lengths of the sides of Lashandra’s triangle?
__________ units, __________ units, __________ units
Answer:
Lashandra used grid paper to construct the triangle which lengths of the sides are number of units.
Let count units: a = 8 units, b = 6 units, c = 10 units.
b. Use the converse of the Pythagorean Theorem to determine whether the triangle is a right triangle.
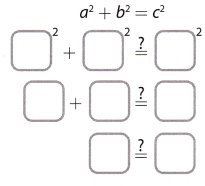
The triangle that Lashandra constructed (is/is not) a right triangle.
Answer:
Using the converse of the Pythagorean Theorem we can determine whether the triangle is a right triangle.
a2 + b2 = c2 …………. (1)
82 + 62 = 102 (Substitute) …………….. (2)
64 + 36 = 100 (Simplify) ………………. (3)
100 = 100 (Add) …………… (4)
As 82 + 62 = 102 the triangle is the right triangle.
Question 2.
A triangle has side lengths 9 cm, 12 cm, and 16 cm. Tell whether the triangle is a right triangle. (Example 1)
Let a = __________, b = __________, and c = __________.
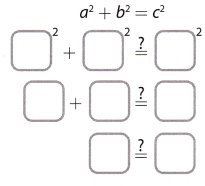
By the converse of the Pythagorean Theorem, the triangle (is/is not) a right triangle.
Answer:
Let a= 9, b = 12 and c = 16.
a2 + b2 = c2 …………. (1)
92 + 122 = 162 (Substitute into formula) ………….. (2)
81 + 144 = 256 (Simplify) ………….. (3)
225 ≠ 256 (Add) …………… (4)
By the converse of the Pythagorean Theorem, the triangle IS NOT a right triangle.
Question 3.
The marketing team at a new electronics company is designing a logo that contains a circle and a triangle. On one design, the triangle’s side lengths are 2.5 in., 6 in., and 6.5 in. Is the triangle a right triangle? Explain. (Example 2)
Answer:
Let a = 2.5in, b = 6m and c = 6.5in.
a2 + b2 = c2 …………. (1)
(2.5)2 + 62 = (6.5)2 (Substitute into formula) ………….. (2)
6.25 + 36 = 42.25 (Simplify) ………………. (3)
42.25 = 42.25 (Add) ………………. (4)
By the converse of the Pythagorean Theorem, the triangle ( is / is not) a right triangle.
The triangle is a right triangle.
Essential Question Check-In
Question 4.
How can you use the converse of the Pythagorean Theorem to tell if a triangle is a right triangle?
Answer:
Knowing the side lengths, we substitute them in the formula a2 + b2 = c2, where c contains the biggest value. If the equation holds true, then the given triangle is a right triangle. Otherwise, it is not a right triangle.
Texas Go Math Grade 8 Lesson 8.2 Independent Practice Answer Key
Tell whether each triangle with the given side lengths is a right triangle.
Question 5.
11 cm, 60 cm, 61 cm
Answer:
Let a = 11, b = 60 and c = 61. Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
112 + 602 = 612
121 + 3600 = 3721
3721 = 3721
True
Since 112 + 602 = 612, the triangle is a right triangle.
Question 6.
5 ft, 12 ft, 15 ft
Answer:
Let a = 5, b = 12 and c = 15 Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
52 + 122 = 152
25 + 144 = 225
169 ≠ 225
False
Since 52 + 122 ≠ 152, the triangle is not a right triangle.
Question 7.
9 in., 15 in., 17 in.
Answer:
Let a = 9 in, b = 15 in, and C = 17 in.
a2 + b2 = c2 ……………….. (1)
92 + 152 = 172 (Substitute into the formula) ………….. (2)
81 + 225 = 289 (Simplify) …………… (3)
306 ≠ 289 (Add) …………… (4)
Since 92 + 152≠ 172, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Question 8.
15 m, 36 m, 39 m
Answer:
Let a = 15m, b = 36m and C = 39m.
a2 + b2 = c2 ……………….. (1)
152 + 362 = 392 (Substitute into the formula) ………….. (2)
225 + 1296 = 1521 (Simplify) ………… (3)
1521 = 1521 (Add) ………….. (4)
Since 152 + 362 = 392, the triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 9.
20 mm, 30 mm, 40 mm
Answer:
Let a = 20mm, b = 30mm and c = 40mm.
a2 + b2 = c2 ……………….. (1)
202 + 302 = 402 (Substitute into the formula) …………. (2)
400 + 900 = 1600 (SimpLify) …………. (3)
1300 ≠ 1600 (Add) …………. (4)
Since 202 + 302 ≠ 402, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Question 10.
20 cm, 48 cm, 52 cm
Answer:
Let a = 20 cm, b = 48 cm and c = 52 cm.
a2 + b2 = c2 ……………….. (1)
202 + 482 = 522 (Substitute into the formula) …………. (2)
400 + 2304 = 2704 (Simplify) …………… (3)
2704 = 2704 (Add) ……………. (4)
Since 202 + 482 = 522, the triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 11.
18.5 ft, 6 ft, 17.5 ft
Answer:
Let a = 6ft, b = 17.5ft and c = 18.5ft.
a2 + b2 = c2 ……………….. (1)
62 + (17.5)2 = (18.5)2 (Substitute into the formula) ……………. (2)
36 + 306.25 = 342.25 (Simplify) ………………. (3)
342.25 = 342.25 (Add) ………….. (4)
Since 62 + (17.5)2 = (18.5)2, the triangle is right triangle by the converse of the Pythagorean Theorem.
Question 12.
2 mi, 1.5 mi, 2.5 mi
Answer:
Let a = 2, b = 1.5 and c = 2.5. Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
22 + 1.52 = 2.52
4 + 2.25 = 6.25
6.25 = 6.25
True
Since 22 + 1.52 = 2.52, the triangle is a right triangle.
Question 13.
35 in., 45 in., 55 in.
Answer:
Let a = 35 in, b = 45 in and c = 55 in.
a2 + b2 = c2 ……………….. (1)
352 + 452 = 552 (Substitute into the formula) …………… (2)
1225 + 2025 = 3025 (Simplify) …………… (3)
3250 ≠ 3025 (Add) ……………. (4)
Since 352 + 452 ≠ 552, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Question 14.
25cm, 14cm, 23cm
Answer:
Let a = 14, b = 23 and c = 25. Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
142 + 232 = 252
196 + 529 = 625
725 = 625
False
Since 142 + 232 ≠ 252, the triangle is not a right triangle.
Question 15.
The emblem on a college banner consists of the face of a tiger inside a triangle. The lengths of the sides of the triangle are 13 cm, 14 cm, and 15 cm. Is the triangle a right triangle? Explain.
Answer:
Let a = 13 cm, b = 14 cm and c = 15 cm.
a2 + b2 = c2 ……………….. (1)
132 + 142 = 152 (Substitute into the formula) ………………. (2)
169 + 196 = 225 (Simplify) ……………. (3)
365 ≠ 225 (Add) …………… (4)
Since 132 + 142 ≠ 152, the triangle is not a right triangle by the converse of the Pythagorean Theorem.
Question 16.
Kerry has a large triangular piece of fabric that she wants to attach to the ceiling in her bedroom. The sides of the piece of fabric measure 4.8 ft, 6.4 ft, and 8 ft. Is the fabric in the shape of a right triangle? Explain.
Answer:
Let a = 4.8 ft, b = 6.4 ft and c = 8 ft
a2 + b2 = c2 ……………….. (1)
(4.8)2 + (6.4)2 = 82 (Substitute into the formula) ……………… (2)
23.04 + 40.96 = 64 (Simplify) ……………. (3)
64 = 64 (Add) ……………… (4)
Since (4.8)2 + (6.4)2 = 82, the triangle is a right triangle by the converse of the Pythagorean Theorem.
The piece of fabric in the shape of a right triangle.
Question 17.
A mosaic consists of triangular tiles. The smallest tiles have side lengths 6 cm, 10 cm, and 12 cm. Are these tiles in the shape of right triangles? Explain.
Answer:
Let a = 6, b = 10 and c = 12. Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
62 + 102 = 122
36 + 100 = 144
136 = 144
False
Since 62 + 102 ≠ 122, the tiles are not in the shape of right triangles.
Question 18.
History In ancient Egypt, surveyors made right angles by stretching a rope with evenly spaced knots as shown. Explain why the rope forms a right angle.

Answer:
Every knote is placed on the equal distance, so the unit of measure ¡s part of the rope between two knotes. Let a = 4 units, b = 3 units, and c = 5 units.
a2 + b2 = c2 ……………….. (1)
42 + 32 = 52 (Substitute into the formula) ……………… (2)
16 + 9 = 25 (Simplify) …………….. (3)
25 = 25 (Add) ……………… (4)
Since 42 + 32 = 52, the triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 19.
Justify Reasoning Yoshi has two identical triangular boards as shown. Can he use these two boards to form a rectangle? Explain.

Answer:
If the triangle boards are right triangles, then Yoshi can form a rectangle. We can use the converse of the Pythagorean Theorem. Let a = 1 m, b = 0.75m and c = 1.25m
a2 + b2 = c2 ……………….. (1)
12 + (0.75)2 = (1.25)2 (Substitute into the formula) ……………….. (2)
1 + 0.5625 = 1.5625 (Simplify) ……………… (3)
1.5625 = 1.5625 (Add) …………….. (4)
Since 12 + (0.75)2 = (1.25)2, triangle boards are right angled by the converse of the Pythagorean Theorem.
Yes, Yoshi can form a rectangle from those triangle boards.
Question 20.
Critique Reasoning Shoshanna says that a triangle with side lengths 17 m, 8 m, and 15 m is not a right triangle because 172 + 82 = 353, 152 = 225, and 353 ≠ 225. Is she correct? Explain.
Answer:
The converse of the Pythagorean Theorem states that if a2 + b2 = c2 (where c is the biggest side length), then the triangle is a right triangle. Using this theorem, we see a = 8, b = 15 and c = 17.
a2 + b2 = c2
82 + 152 = 172
64 + 225 = 289
289 = 289
True
Since 82 + 152 = 172, the triangle is a right triangle. Shoshanna was incorrect because she used the formula c2 + a2 = b2, which is not the correct formula of the Pythagorean Theorem.
H.O.T. Focus on Higher Order Thinking
Question 21.
Make a Conjecture Diondre says that he can take any right triangle and make a new right triangle just by doubling the side lengths. Is Diondre’s conjecture true? Test his conjecture using three different right triangles.
Answer:
Given a right triangle, the Pythagorean Theorem holds. Therefore,
a2 + b2 = c2
If we double the side lengths of that triangle, we get:
(2a)2 + (2b)2 = (2c)2
4a2 + 4b2 = 4c2
4(a2 + b22) = 4c2
a2 + b2 = c2
As we can see, doubling the side lengths of a right triangle would create a new right triangle.
We can test that by using three different right triangles.
The triangle with sides a = 3, b = 4 and c = 5 is a right triangle. We double its sides and check if the new triangle is a right triangle. We get a = 6, b = 8, c = 10.
62 + 82 = 102
36 + 64 = 100
100 = 100
True
Since 62 + 82 = 102, the new triangle is a right triangle by the converse of the Pythagorean Theorem.
The triangle with sides a = 6, b = 8 and c = 10 is a right triangle. We double its sides and check if the new triangle is a right triangle. We get a = 12, b = 16, c = 20.
122 + 162 = 202
144 + 256 = 400
400 = 400
True
Since 122 + 162 = 202, the new triangle is a right triangle by the converse of the Pythagorean Theorem.
The triangle with sides a = 12, b = 16 and c = 20 is a right triangle. We double its sides and check if the new triangle is a right triangle. We get a = 24, b = 32, c = 40.
242 + 322 = 402
576 + 1024 = 1600
1600 = 1600
True
Since 242 + 322 = 402, the new triangle is a right triangle by the converse of the Pythagorean Theorem.
Question 22.
Draw Conclusions A diagonal of a parallelogram measures 37 inches. The sides measure 35 inches and 1 foot. Is the parallelogram a rectangle? Explain your reasoning.
Answer:
A rectangle is a parallelogram where the interior angles are right angles. To prove if the given parallelogram is a rectangle, we need to prove that the triangle formed by the diagonal of the parallelogram and two sides of it, is a right triangle. Converting all the values into inches, we have a = 12, b = 35 and c = 37 Using the converse of the Pythagorean Theorem, we have:
a2 + b2 = c2
122 + 352 = 372
144 + 1225 = 1369
1369 = 1369
True
Since 122 + 352 = 372, the triangle is a right triangle. Therefore, the given parallelogram is a rectangle.
Question 23.
Represent Real-World Problems A soccer coach is marking the lines for a soccer field on a large recreation field. The dimensions of the field are to be 90 yards by 48 yards. Describe a procedure she could use to confirm that the sides of the field meet at right angles.
Answer:
To confirm that the sides of the field meet at right angles, she could measure the diagonaL of the fieLd and use the converse of the Pythagorean Theorem. If a2 + b2 = c2 (where a = 90, b = 48 and c is the length of the diagonal), then the triangle is a right triangle. This method can be used for every corner to decide if they form right angles or not.