Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 7.2 Answer Key Angle Theorems for Triangles.
Texas Go Math Grade 8 Lesson 7.2 Answer Key Angle Theorems for Triangles
Texas Go Math Grade 8 Lesson 7.2 Explore Activity Answer Key
Explore Activity 1
Sum of the Angle Measures in a Triangle
There is a special relationship between the measures of the interior angles of a triangle.
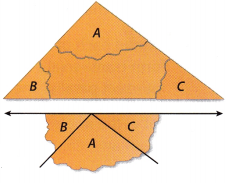
A. Draw a triangle and cut it out. Label the angles A, B, and C.
B. Tear off each “corner” of the triangle. Each corner includes the vertex of one angle of the triangle.
C. Arrange the vertices of the triangle around a point so that none of your corners overlap and there are no gaps between them.
D. What do you notice about how the angles fit together around a point?
E. What is the measure of a straight angle?
F. Describe the relationship among the measures of the angles of △ ABC.
The Triangle Sum Theorem states that for △ ABC, m∠A + m∠B + m∠C = _________.
Reflect
Question 1.
Justify Reasoning Can a triangle have two right angles? Explain.
Answer:
We already know that all angles of a triangle add up to 180°. If the first two angles add up to 180° (2 right angles, 90° each), it means that the third one must measure 0°, which does not make sense. Therefore, a triangle cannot have two right angles.
Question 2.
Analyze Relationships Describe the relationship between the two acute angles in a right triangle. Explain your reasoning.
Answer:
A right triangle is a triangle that has one right angle and two other acute angles. Since we know that all angles of a triangle add up to 180°, and we have one angle of 90° in a right triangle, it means that the sum of the other two acute angles will be 90° (180° – 90°).
Explore Activity 2
Justifying the Triangle Sum Theorem
You can use your knowledge of parallel lines intersected by a transversal to informally justify the Triangle Sum Theorem.
Follow the steps to informally prove the Triangle Sum Theorem. You should draw each step on your own paper. The figures below are provided for you to check your work.
A. Draw a triangle and label the angles as ∠1, ∠2, and ∠3 as shown.

B. Draw line a through the base of the triangle.
C. The Parallel Postulate states that through a point not on a line 2, there is exactly one line parallel to line 2. Draw line b parallel to line o, through the vertex opposite the base of the triangle.
D. Extend each of the non-base sides of the triangle to form transversal s and transversal t. Transversals s and t intersect parallel lines a and b.
E. Label the angles formed by line b and the transversals as ∠4 and ∠5.

F. Because ∠4 and ___________ are alternate interior angles, they are ____________.
Label ∠4 with the number of the angle to which it is congruent.
G. Because ∠5 and ___________ are alternate interior angles, they are ____________.
Label ∠5 with the number of the angle to which it is congruent.
H. The three angles that lie along line b at the vertex of the triangle are ∠1, ∠4, and ∠5. Notice that these three angles lie along a line.
So, m∠1 + m∠4 + m∠5 = ______________
Because angles 2 and 4 are congruent and angles 3 and 5 are congruent, you can substitute m∠2 for m∠4 and m∠3 for m∠5 in the equation above.
So, m∠1 + m∠2 + m∠3 = ______________
This shows that the sum of the angle measures in a triangle is always _____________.
Reflect
Question 3.
Analyze Relationships How can you use the fact that m∠4 + m∠1 + m∠5 = 180° to show that m∠2 + m∠1 + m∠3 = 180°?
Answer:
m∠4 + m∠1 – m∠5 = 180° ………….. (1)
m∠2 = m∠4 since ∠2 and ∠4 are alternate interior angles
m∠3 = m∠5 since ∠3 and ∠5 are alternate interior angles
Therefore, we substitute m∠2 for m∠4 and m∠3 for m∠5 in equation (1) and we get:
m∠2 + m∠1 + m∠3 = 180° …………….. (2)
Your Turn
Find the missing angle measure.
Question 4.
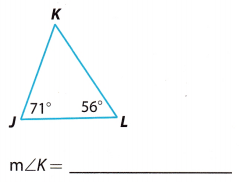
Answer:
From the Triangle Sum Theorem we have:
m∠J + m∠L +m∠K = 1800
We substitute the given angle measures and we solve for m∠K.
71° + 56° + m∠K = 180°
127° + m∠K = 180°
127° – 127° + m∠K = 180° – 127°
m∠K = 53°
Question 5.
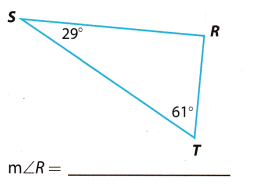
Answer:
To determine the answer here, we will use the following rule:
α + β + γ = 180°
where α, β and γ are angles in a triangle.
Therefore, we know the following:
m∠S = 29°
m∠T = 61°
m∠R =?
Using the rule given in step 1, we can compute as following:
m∠S + m∠T + m∠R = 180°
29° + 610 + m∠R = 180°
m∠R = 180° – 29° – 61°
m∠R = 90°
Hence, the missing angle measure is:
m∠R = 90°
Explore Activity 3
Exterior Angles and Remote Interior Angles
An interior angle of a triangle is formed by two sides of the triangle. An exterior angle is formed by one side of the triangle and the extension of an adjacent side. Each exterior angle has two remote interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle.
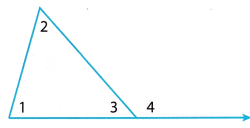
- ∠1, ∠2, and ∠3 are interior angles.
- ∠4 is an exterior angle.
- ∠1 and ∠2 are remote interior angles to ∠4.
There is a special relationship between the measure of an exterior angle and the measures of its remote interior angles.
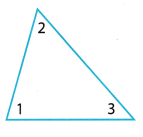
A. Extend the base of the triangle and label the exterior angle as ∠4.
B. The Triangle Sum Theorem states: m∠1 + m∠2 + m∠3 = ____________.
C. ∠3 and ∠4 form a ____________,
so m∠3 + m∠4 = _____________.
D. Use the equations in B and c to complete the following equation:
m∠1 + m∠2 + _________ = _________ + m∠4
E. Use properties of equality to simplify the equation in D: _____________
The Exterior Angle Theorem states that the measure of an _________ angle is equal to the sum of the measure of its ___________ angles.
Reflect
Question 6.
Sketch a triangle and draw all of its exterior angles. How many exterior angles does a triangle have at each vertex?
Answer:
Angles ∠1, ∠2 and ∠3 are interior angles.
∠4 and ∠5 are exterior angles for ∠1.
∠6 and ∠7 are exterior angles for ∠2.
∠8 and ∠9 are exterior angles for ∠3.
So, we have two exterior angles at each vertex.
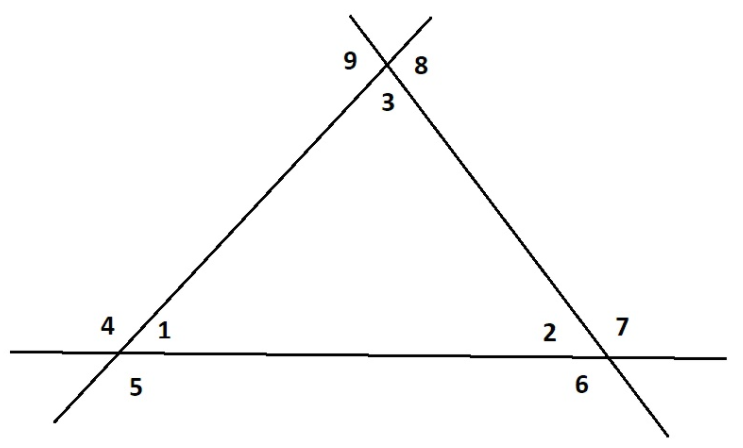
Question 7.
How many total exterior angles does a triangle have?
Answer:
There are two exterior angles at each of three vertex, so we have total 6 exterior angles.
Your Turn
Question 8.
Find m∠M and m∠N.
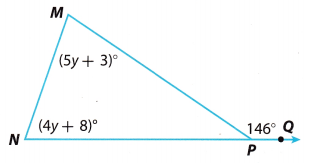
m∠M = ____________
m∠N = ____________
Answer:
Using the Exterior Angle Theorem we have:
m∠M + m∠N = m∠MPQ
We substitute the given angle measures and we solve the equation for y
(5y + 3)°+(4y + 8)° = 146°
5y° + 3° + 4y° + 8° = 146°
9y° + 11° = 146°
9y° + 11° – 11° = 146° – 11°
9y° = 135°
\(\frac{9 y^{\circ}}{9^{\circ}}=\frac{135^{\circ}}{9^{\circ}}\)
y = 15
We use the value of y to find m∠M and m∠N.
m∠M = (5y + 3)° = (5 ∙ 15 + 3)° = 78°
m∠M = 78°
m∠N = (4y + 8)° = (4 ∙ 15 + 8)° = 68°
m∠N = 68°
Texas Go Math Grade 8 Lesson 7.2 Guided Practice Answer Key
Find each missing angle measure. (Explore Activity 1 and Example 1)
Question 1.
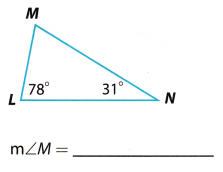
Answer:
From the Triangle Sum Theorem we have:
m∠L + m∠N + m∠M = 180°
We substitute the given angle measures and we solve for m°M.
78° + 31° + m∠M = 180°
109° + m∠M = 180°
109° – 109° + m∠M = 180° – 109°
m∠M = 71°
Question 2.

Answer:
From the Triangle Sum Theorem we have:
m∠Q + m∠S + m∠R = 180°
We substitute the given angle measures and we solve for m∠Q.
m∠Q + 24° + 126° = 180°
m∠Q + 150° = 180°
m∠Q + 150° – 150° = 180° – 150°
m∠Q = 30°
Use the Triangle Sum Theorem to find the measure of each angle in degrees. (Explore Activity 2 and Example 1)
Question 3.
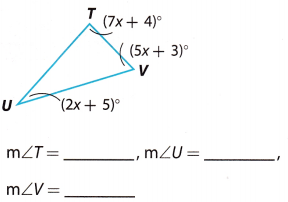
Answer:
From the Triangle Sum Theorem we have:
m∠U + m∠T +m∠V = 180°
We substitute the given angle measures and we solve for x
(2x + 5)° + (7x + 4)° + (5x + 3)° = 180°
2x° + 5° + 7x° + 4° + 5x° + 3° = 180°
14x° + 12° = 180°
14x° + 12° – 12° = 180° – 12°
14x° = 168°
\(\frac{14 x^{\circ}}{14^{\circ}}=\frac{168^{\circ}}{14^{\circ}}\)
x = 12
We use the value of x to find the angles.
m∠U = (2x + 5)° = (2 ∙ 12 + 5)° = 29°
m∠U = 29°
m∠T = (7x + 4)° = (7 ∙ 12 + 4)° = 88°
m∠T = 88°
m∠V = (5x + 3)° = (5 ∙ 12 + 3)° = 63°
m∠V = 63°
Question 4.
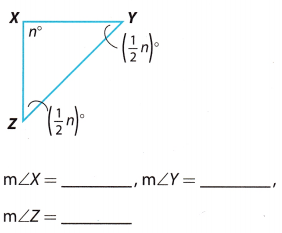
Answer:
From the Triangle Sum Theorem we have:
m∠X + m∠Y + m∠Z = 180°
We substitute the given angle measures and we soLve for n.
n° + (\(\frac{1}{2}\)n)° + (\(\frac{1}{2}\)n)° = 180°
2n° = 180°
\(\frac{2 n^{\circ}}{2^{\circ}}=\frac{180^{\circ}}{2^{\circ}}\)
n = 90
We use the value of n to find the angles.
m∠X = n° = 90°
m∠X = 90°
m∠Y = (\(\frac{1}{2}\)n)° = (\(\frac{1}{2}\) ∙ 90)° = 45°
m∠Y = 45°
m∠Z = (\(\frac{1}{2}\)n)° = (\(\frac{1}{2}\) ∙ 90)° = 45°
m∠Z = 45°
Use the Exterior Angle Theorem to find the measure of each angle in degrees. (Explore Activity 3 and Example 2)
Question 5.
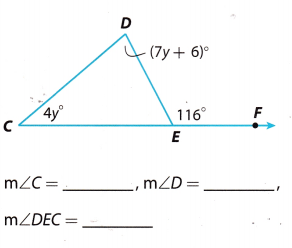
Answer:
Write the Exterior Angle Theorem as it applies to this triangle.
∠C + ∠D = ∠DEF ……………… (1)
4y° + (7y + 6)° = 116° (Substitute the given angle measures) …………. (2)
4y° + 7y° + 6° = 116° (Remove parentheses) ……………. (3)
11y° + 6° = 116° (Simplify) ………… (4)
11y° = 116° – 6° (Take 6 from both sides) …………….. (5)
11y° = 110° (Simplify) ……………. (6)
y° = \(\frac{110}{11}\) (Divide both sides by 11) ………… (7)
y° = 10° (Simplify) ………… (8)
Now, we can calculate the measure of the angles:
m∠C = 4 ∙ 10° = (4 ∙ 10)° = 40°
m∠D = (7y + 6)° (7 ∙ 10 + 6)° = (70 + 6)° = 76°
m∠DEC = 180° – 116° = 64°
Question 6.

Answer:
Using the Exterior Angle Theorem we have:
m∠M + m∠L = m∠JKM
We substitute the given angle measures and we solve the equation for z.
(5z – 3)° + (18z + 3)° = 161°
5z° – 3 + 18z° + 3° = 161°
23z° = 161°
\(\frac{23 z^{\circ}}{23^{\circ}}=\frac{161^{\circ}}{23^{\circ}}\)
z = 7
We use the value of z to find m∠M and m∠L.
m∠M = (5z – 3)° = (5 ∙ 7 – 3)° = 32°
m∠M = 32°
m∠L = (18z + 3)° = (18 ∙ 7 + 3)° = 129°
m∠L = 129°
From the Triangle Sum Theorem we have:
m∠M + m∠L + m∠LKM = 180°
We substitute the given angle measures and we solve for m∠LKM
32° + 129° + m∠LKM = 180°
161° + m∠LKM = 180°
161° – 161° + m∠LKM = 180° – 161°
m∠LKM = 19°
Essential Question Check-In
Question 7.
Describe the relationships among the measures of the angles of a triangle.
Answer:
The sum of all, measures of the interior angles of a triangle is 180°
The measure of an exterior angle of a triangle is equal to the sum of its remote interior angles.
Texas Go Math Grade 8 Lesson 7.2 Independent Practice Answer Key
Find the measure of each angle.
Question 8.
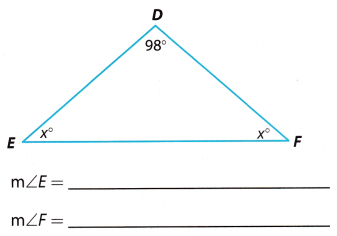
Answer:
By the triangle sum theorem, sum of the angles of the triangle is 180°
∠D + ∠E + ∠F = 180° ………………. (1)
98° + x° + X° = 180° (Substitute the measures of the angles) ……………… (2)
98° + 2x° = 180° (Simplify) ………….. (3)
2x° = 180° – 98° (Take 98° from both sides) ………….. (4)
2x° = 82° (Simplify) …………….. (5)
x° = \(\frac{82}{2}\) (Divide both sides by 2) …………….. (6)
x° = 41° (Simplify) ……………. (7)
m∠E = 41°
m∠F = 41°
Question 9.
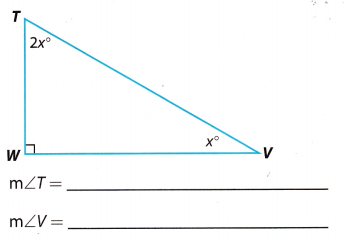
Answer:
Angles of the triangle are m∠W = 90°, m∠V = X° and m∠T = 2x°.
By the triangLe sum theorem, sum of the angles of the triangle is 180°
∠W + ∠V + ∠T = 180° ……………… (1)
90° + x° + 2x° = 180° (Substitute the measures of the angles) …………… (2)
90° + 3x° = 180° (Simplify) ………… (3)
3x° = 180° – 90° (Take 90° from both sides) …………….. (4)
3x° = 90° (Simplify) …………… (5)
x° = \(\frac{90}{3}\) (Divide both sides by 3) …………… (6)
x° = 30° (Simplify) …………. (7)
m∠T = 2x° = (2 ∙ 30)° = 60°
m∠T = 60°
m∠V = 30°
Question 10.

Answer:
Angles of the triangle are m∠G = 5x°, m∠H = 4x° and m∠J = 3x°.
By the triangle sum theorem, sum of the angles of the triangle is 180°
∠G + ∠H + ∠J = 180° ………………. (1)
5x° + 4x° + 3x° = 180° (Substitute the measures of the angles) …………… (2)
12x° = 180° (Simplify) ……………. (3)
x° = \(\frac{180}{12}\) (Divide both sides by 12) ……………. (4)
x° = 15° (Simplify) ………………. (5)
m∠G = 5x° = (5 ∙ 15)° = 75°
m∠H = 4x° = (4 ∙ 15)° = 60°
m∠U = 3x° = (3 ∙ 15)° = 45°
Question 11.

Answer:
Write the Exterior Angle Theorem as it applies to this triangle.
∠Q + ∠P =∠QRS …………….. (1)
(3y + 5)° + (2y – 7)° = 153° (Substitute the given angle measures) …………… (2)
3y° + 5° + 2y° – 7° = 153° (Remove parentheses) ……………. (3)
5y° – 2° = 153° (Combine like terms) ……………. (4)
5y° = 153° + 2° (Add 2 to both sides) …………… (5)
5y° = 155° (Simplify) …………… (6)
y° = \(\frac{155}{5}\) (Divide both sides by 5) ………………. (7)
y° = 31° (Simplify) …………… (8)
Now, we can calculate the measure of the angles:
m∠Q = (3y + 5)° = (3 ∙ 31 + 5)° = (93 + 5)° = 98°
m∠P = (2y – 7)° = (2 ∙ 31 – 7)° = (62 – 7)° = 55°
m∠QRP = 180° – 153° = 27°
Question 12.

Answer:
Using Triangle sum theorem we have
m∠A + m∠B + m∠ACB = 180° ……………. (1)
78° + 58° + m∠AGB = 180° (Substitute measures of the angle into the formula) ………….. (2)
136° + m∠ACB = 180° (Simplify) ……………. (3)
m∠ACB = 180° – 136° (Take 136° from both sides) ………… (4)
m∠ACB = 44° …………… (5)
Now, let’s find measure of the angle m∠DCE
m∠D + m∠E + m∠DCE = 180° ………….. (6)
85° + 60° + m∠DCE = 180° (Substitute measures of the angle into the formula) …………… (7)
145° + m∠DCE = 180° (Simplify) …………….. (8)
m∠DCE = 180° – 145° (Take 136° from both sides) ……………… (9)
m∠DCE = 35° ……………….. (10)
As we can see,
m∠ACB + m∠BCD + m∠DCE = 180° …………….. (11)
44° + m∠BCD + 350 = 180° (Substitute measures of the angle into the formula) ……………. (12)
79° + m∠BCD = 180° (Simplify) ……………. (13)
m∠BCD = 180° – 79° (Take 79° from both sides) ………….. (14)
m∠BCD = 101° ………………. (15)
Question 13.

Answer:
Angles of the triangle are m∠K = 2x°, m∠L = 3x° and m∠KML = 3x°.
By the triangle sum theorem, sum of the angles of the triangle is 180°.
∠K + ∠L + ∠KML = 180° …………… (1)
2x° + 3x° + x° = 180° (Substitute the measures of the angles) …………….. (2)
6x° = 180° (Simplify) ……………. (3)
x° = \(\frac{180}{6}\) (Divide both sides by 6) …………… (4)
x° = 30° (Simplify) ………… (5)
m∠K = 2x° = (2 ∙ 30)° = 60°
m∠L = 3x° = (3 ∙ 30)° = 90°
m∠KML = x° = 30°
Angle m∠LMN is supplementary with m∠KML so we have
m∠KML + m∠LMN = 180° ………………….. (6)
30° + m∠LMN = 180° (Substitute) …………… (7)
m∠MN = 180° – 30° (Take 30° from both sides) ………… (8)
m∠LMN = 150° (Simplify) …………….. (9)
m∠K = 60°
m∠L = 90°
m∠KML = 30°
m∠LMN = 150°
Question 14.
Multistep The second angle in a triangle is five times as large as the first. The third angle is two-thirds as large as the first. Find the angle measures.
Answer:
Lets name the interior angLes of the triangle ∠1, ∠2 and ∠3. As we don’t know the measure of any angle in a triangle, Lets put ∠1 = x.
Angle ∠2 is five times as large as the first, so
∠2 = 5 ∙ ∠1 (Substitute ∠1 = x)
= 5x
Angle ∠3 is two-thirds as large as the first, so
∠3 = \(\frac{2}{3}\) ∙ ∠1 (Substitute ∠1 = x)
= \(\frac{2}{3}\)x
By Triangle Sum Theorem

Question 15.
Analyze Relationships Can a triangle have two obtuse angles? Explain.
Answer:
An obtuse angle is a type of angle which measure greater than 90° but Less than 180°.
In the question “Can a triangle have two obtuse angles?”, the answer is no If one of the interior angles of a triangle is an obtuse angle, it follows that the other two remaining interior angles are both acute angles. It is because the sum of the interior angles of a triangle is 180°. So, it is impossible to have two obtuse angles in the interior angles of a triangle.
H.O.T. Focus on Higher Order Thinking
Question 16.
Critical Thinking Explain how you can use the Triangle Sum Theorem to find the measures of the angles of an equilateral triangle.
Answer:
All angles have the same measure ¡n an equilateral triangle
Using the Triangle Sum Theorem, you can name all angles
∠x
∠x + ∠x + ∠x = 180
then simplify to
3(∠x) = 180
and solve for ∠x
Question 17.
a. Draw Conclusions Find the sum of the measures of the angles in quadrilateral ABCD.
(Hint: Draw diagonal \(\overline{A C}\). How can you use the figures you have formed to find the sum?)
Sum = ____________
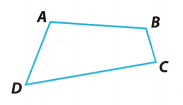
Answer:
Lets find the sum of the measures of the angles in quadrilateral ABCD. If we draw diagonal \(\overline{A C}\), we form two triangles ABC and ADC. By the Triangle Sum Theorem
∠DAC + ∠D + ∠DCA = 180° ………………. (1)
∠CAB + ∠B + ∠BCA = 180° ………………. (2)
Notice that ∠A = ∠DAC + ∠CAB and ∠C = ∠DCA + ∠BCE
So, the sum of the measures of the angles in quadrilateral ABCD is
∠A + ∠B + ∠C + ∠D = ∠DAC + ∠CAB + ∠B + ∠DCA + ∠BCA + ∠D ……………….. (3) Substitute
= (∠DAC + ∠D + ∠DCA) + (∠CAB + ∠B + ∠BCA) ……………….. (4) (Combine angles triangles ABC and ADC)
= 180°+ 180° …………… (5) (By Triangle Sum Theorem)
= 360° ………………. (6) (Simplify)
b. Make a Conjecture Write a “Quadrilateral Sum Theorem.” Explain why you think it is true.
Answer:
“Quadrilateral. Sum Theorem:” The sum of the angle measures of quadrilateral is 360°. According to a. every quadrilateral can be divided by diagonal to two triangles, so the sum of angles is 180° + 180° = 360°.
Question 18.
Communicate Mathematical Ideas Describe two ways that an exterior angle of a triangle is related to one or more of the interior angles.
Answer:
An exterior angle is formed by one side of the triangLe and the extension of an adjacent side Each exterior angle has two remote interior angles that are not adjacent to the exterior angle.
An exterior angle is related to the interior angles of a triangle First, the relationship is that the exterior angle is supplementary to its adjacent interior angle. The sum of their angles is 180°.
Another relationship is that the sum of the two remote interior angles which are not adjacent to the exterior angle is equal to the measure of the exterior angle.