Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Module 9 Quiz Answer Key.
Texas Go Math Grade 7 Module 9 Quiz Answer Key
Texas Go Math Grade 7 Module 9 Ready to Go On? Answer Key
9.1 Angle Relationships
Use the diagram to name a pair of each type of angle.
Question 1.
Supplementary angles _____
Answer:
∠DFC and ∠BFC
Question 2.
Complementary angles. _____
Answer:
∠AFB and ∠BFC
Question 3.
Vertical angles. _____
Answer:
∠EFD and ∠BFC
9.2, 9.3 Finding Circumference and Area of Circles
Find the circumference and area of each circle. Use 3.14 for π.
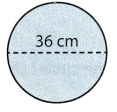
Question 4.
Circumference ≈ _____
Answer:
d = 36 cm
Use the formula for the circumference of the circle when given diameter
C = π(d) Substitute 36 for d, and 3.14 for π.
C ≈ 3.14(36)
C ≈ 113.04
The circumference of the circle is 113.04 cm
C ≈ 113.04 cm
Question 5.
area ≈ ___
Answer:
Use the formula for the area of the circle.
Since the diameter is twice a radius, the formula for area of a circle, when given the diameter, is
A = π\(\left(\frac{d}{2}\right)^{2}\) Substitute 36 for d, and 3.14 for π.
A ≈ 3.14 . \(\left(\frac{36}{4}\right)^{2}\)
A ≈ 3.14 182
A ≈ 3.14 . 324
A ≈ 1017.36
The area of the circle is about 1017.36 cm2.
A ≈ 1017.36 cm2
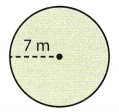
Question 6.
Circumference ≈ _____
Answer:
The radius of the circle is 7 m.
Use the formula for the circumference of the circle.
C = 2π(r) Substitute 7 for r, and \(\frac{22}{7}\) for π.
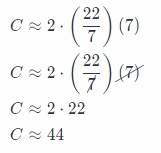
The circumference is about 44 m.
C ≈ 44
Question 7.
area ≈ ___
Answer:
Use the formula for the area of the circle
A = Substitute 7 for r, and 314 for w.
A ≈ 3.14(7)2
A ≈ 3.14 49
A ≈ 153.86
The area of the circle is about 153.86 m2
A ≈ 153.86 m2.
9.4 Area of Composite Figures
Find the area of each figure. Use 3.14 for π.
Question 8.

Answer:
Separate the figure into a triangle and one semicircle.
Area of the triangle
base = 14 m
height = 10 m
Use the formula for the area of the triangLe.
A1 = \(\frac{1}{2} b \cdot h\)
A1 = \(\frac{1}{2} 14 \cdot 10\)
A1 = \(\frac{70}{2}\)
A1 = 35
The area of the triangle is 35 m2.
Area of the circle
diameter = 14 m
Use the formula for the area of the circte when given diameter
Ac = \(\pi\left(\frac{d}{2}\right)^{2}\) Subsitute 14 for d and 3.14 for π.
Ac = 3.14\(\left(\frac{14}{2}\right)^{2}\)
Ac = 3.14 . 72
Ac = 3.14 . 49
Ac = 153.86
Area of the semicircle is half the area of the circle.
A2 = \(\frac{A_{c}}{2}\) = \(\frac{153.86}{2}\) = 76.93
The area of the semicircle is 76.93 m2.
Add the areas to find the total area.
A = A1 + A2 = 35 + 76.93 = 111.93
The area of the figure is 111.93 m2.
Question 9.
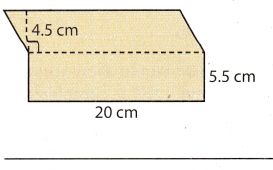
Answer:
Separate the figure into a rectangle and a parallelogram.
Area of the rectangle
length = 20 cm
width = 5.5 cm
Use the formula for the area of the rectangle.
A1 = l . w
A1 = 20 . 5.5
A1 = 110
The area of the rectangle is 110 cm2.
Area of the paralleogram
b = 20 cm
h = 4.5 cm
Use the formula for the area of the paralleogram.
A2 = b . h
A2 = 20 . 4.5
A2 = 90
The area of the parallelogram is 90 cm2
Add the areas to find the total area.
A = A1 + A2 = 110 + 90 = 200
The area of the figure is 200 cm2.
Essential Question
Question 10.
How can you use geometric formulas in real-world situations?
Answer:
There are times that we need to determine the area or perimeter or volume of a certain object or even a place and
the only given is the dimensions, the geometric formuLas are very helpful in such a way that we can calculate it by ourselves.
The geometric formulas are very helpful.
Texas Go Math Grade 7 Module 9 Mixed Review Texas Test Prep Answer Key
Selected Response
Use the diagram for Exercises 1-3.
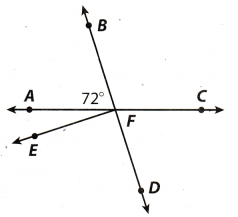
Question 1.
What is the measure of ∠BFC?
(A) 18°
(B) 72°
(C) 108°
(D) 144°
Answer:
(C) 108°
Explanation:
∠AFB and ∠BFC are supplement angles, hence
∠AFB + ∠BFC = 180° Substitute 72° for ∠AFB
72° + ∠BFC = 180° Subtract 72° from both sides.
∠BFC = 180° – 72°
∠BFC = 108°
Question 2.
Which describes the relationship between ∠BFA and ∠CFD?
(A) adjacent angles
(B) complementary angles
(C) supplementary angles
(D) vertical angles
Answer:
(D) vertical angles
Question 3.
Which information would allow you to identify ∠BFA and ∠AFE as complementary angles?
(A) m∠AFE = 108°
(B) ∠DFE is a right angle.
(C) ∠BFA and ∠BFC are supplementary angles.
(D) ∠BFA and ∠BFC are adjacent angles.
Answer:
(B) ∠DFE is a right angle.
Explanation:
∠DFE is a right angle, as we see in the diagram.
Question 4.
David pays $7 per day to park his car. He uses a debit card each time. By what amount does his bank account change due to parking charges over a 40-day period?
(A) -$280
(B) -$47
(C) $47
(D) $280
Answer:
(A) -$280
Explanation:
David pays $7 each day for 40 days, so amount on his bank account decreases for $7 . 40 = $280.
Question 5.
What is the circumference of the circle? Use 3.14 for π.
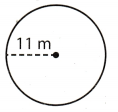
(A) 34.54 m
(B) 69.08 m
(C) 379.94 m
(D) 1,519.76 m
Answer:
(B) 69.08 m
Explanation:
r = 11 m
Use the formula for circumference.
C = 2πr(r) Substitute 11 for r and 314 for π
C ≈ 2 3.14 . 11
C ≈ 69.08
The circumference of the circle is 69.08 m.
Question 6.
What is the area of the circle? Use 3.14 for π.
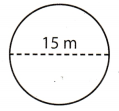
(A) 23.55 m2
(B) 176.625 m2
(C) 47.1 m2
(D) 706.5 m2
Answer:
(B) 176.625 m2
Explanation:
d = 15m
Use the formula for the area of the circle.
A = πr2
Since the diameter is twice a radius, the formula for area of a circle, when given the diameter, is
A = π(r)2 Substitute \(\frac{d}{2}\) for r.
A = \(\pi\left(\frac{d}{2}\right)^{2}\) Substitute 15 for d, and 3.14 for π.
A ≈ 3.14 . \(\left(\frac{15}{2}\right)^{2}\)
A ≈ 3.14 . (7.5)2
A ≈ 3.14 . 56.25
A ≈ 176.62
The area of the circle is about 176.62 m2.
Gridded Response
Question 7.
Find the area in square meters of the figure below? Use 3.14 for π.
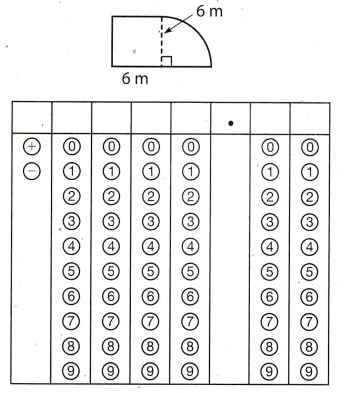
Answer:
Separate the figure into square and a quater of circle.
Area of the square
side = 6 m
Use the formula for the area of the square
A1 = 82
A1 = 62
A1 = 36
The area of the sqaure is 36 m2.
To find the area of the quarter of a circle, find the area of the circle and divide it by 4.
Area of the circle
radius = 6 m
Use the formula for the area of the circle when given radius.
Ac = πr2 Subsitute 10 for r and 314 for w.
Ac = 3.14(6)2
Ac = 3.14 . 36
Ac = 113.04
A2 = \(\frac{A_{c}}{4}\) = \(\frac{113}{404}\) = 28.26
The area of the quarter of the circle is 28.26 m2.
Add the areas to find the total area.
A = A1 + A2 = 36 + 28.26 = 64.26
The area of the figure is 64.26 m2.