Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 9.2 Answer Key Finding Circumference.
Texas Go Math Grade 7 Lesson 9.2 Answer Key Finding Circumference
Essential Question
How do you find the circumference of a circle?
Example 1
Find the circumference of the circle to the nearest hundredth. Use 3.14 or \(\frac{22}{7}\) for π.
Step 1
Identify the diameter of the circle.
d = 8 in.
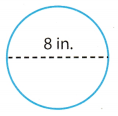
Step 2
Use the formula.
C = πd
C = π(8) Substitute 8 for d.
C ≈ 3.14(8) Substitute 3.14 for π.
C ≈ 25.12 Multiply.
The circumference is about 25.12 inches.
Reflect
Question 1.
What value of π could you use to estimate the circumference? ____
Answer:
We could use 3.14 or \(\frac{22}{7}\).
Question 2.
Checking for Reasonableness How do you know your answer is reasonable?
Answer:
The answer would be reasonable as the value of π is close to the actual result. We could not use the real value of π because it is non-terminating decimal. It is better to use a round-off value for π.
The result is closer to the actual value.
Your Turn
Question 3.
Find the circumference of the circle to the nearest hundredth.
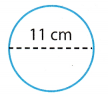
Answer:
Diameter of the circle is 11 cm
Use the formula for the circumference of the circle
C = π(d) Substitute 11 for d, and 3.14 for π.
C ≈ 3.14(11)
C ≈ 34.54
The circumference is about 34.54 cm.
C ≈ 34.54 cm
Example 2
An irrigation sprinkler waters a circular region with a radius of 14 feet. Find the circumference of the region watered by the sprinkler. Use \(\frac{22}{7}\) for π.
Use the formula.

The circumference of the region watered by the sprinkler is about 88 feet.
Reflect
Question 4.
Analyze Relationships When is it logical to use \(\frac{22}{7}\) instead of 3.14 for π?
Answer:
We use \(\frac{22}{7}\) when the length of the diameter(or the radius) is divisible by 7, so that we can shorten 7 from the fraction \(\frac{22}{7}\).
Your Turn
Question 5.
Find the circumference of the circle.
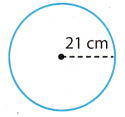
Answer:
The radius of the circle is 21 cm.
Use the formula for the circumference of the circle
C = 2π(r) Substitute 21 for r, and \(\frac{22}{7}\) for π.
C ≈ 2 . (\(\frac{22}{7}\))(21)
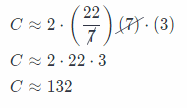
The circumference is about 132 cm.
C ≈ 132 cm
Example 3.
A circular pond has a circumference of 628 feet. A model boat is moving directly across the pond, along a radius, at a rate of 5 feet per second. How long does it take the boat to get from the edge of the pond to the center?
Step 1
Find the radius of the pond.

The radius is about 100 feet.
Step 2
Find the time it takes the boat to get from the edge of the pond to the center along the radius. Divide the radius of the pond by the speed of the model boat.
1oo ÷ 5 = 20
It takes the boat about 20 seconds to get to the center of the pond.
Reflect
Question 6.
Analyze Relationships Dante checks the answer to Step 1 by multiplying it by 6 and comparing it with the given circumference. Explain why Dante’s estimation method works. Use it to check Step 1.
Answer:
Dantes estimation method works because since the value of 2π when rounded off is equal to 6.
Since 2π = 6.28 ≈ 6, and r = \(\frac{C}{2 \pi}\), we have
r ≈ \(\frac{C}{6}\) ⇒ C = 6r.
Lets check the estimation:
6 . 100 = 600 ≈ 628 = C.
The value of 2π when rounded off is equal to 6.
Question 7.
What If? Suppose the model boat were traveling at a rate of 4 feet per second. How long would it take the model boat to get from the edge of the pond to the center? _________________________________________
Answer:
The radius is about 100 feet
We have to divide the radius by the speed of the boat, which is 4 feet per second.
Hence,
100 ÷ 4 = 25
Boat needs about 25 seconds to get to the center of the pond
Your Turn
Question 8.
A circular garden has a circumference of 44 yards. Lars is digging a straight line along a diameter of the garden at a rate of 7 yards per hour. How many hours will it take him to dig across the garden?
Answer:
From the formula for the circumference of the circle we find the diameter of the garden.
C = π(d) Substitute 44 for C, and 3.14 for π
44 ≈ 3.14 . (d) Divide both sides by 3.14
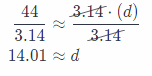
The diameter is about 14 yards.
To find the time which wiLl take Lars to dig across the garden, we divide the diameter of the garden by the speed of digging, 14 ÷ 7 = 2.
It will take him 2 hours to dig the garden.
Texas Go Math Grade 7 Lesson 9.2 Guided Practice Answer Key
Find the circumference of each circle. (Examples 1 and 2)
Question 1.
C = πd
C ≈ ___
C ≈ inches
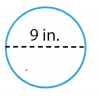
Answer:
The diameter of the circle is 9 inches.
C = π(d) Substitute 9 for d and 3.14 for π
C ≈ 3.14(9)
C ≈ 28.26
The circumference is about 28.26 inches.
C ≈ 28.26 inches.
Question 2.
C ≈ 2πr
C ≈ \(2\left(\frac{22}{7}\right)\) (_______)
C ≈ ___ cm
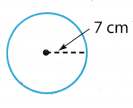
Answer:
The radius of the circle is 7 cm.
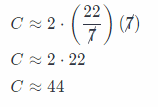
The circumference is about 44 cm.
C ≈ 44 cm
Find the circumference of each circle. Use 3.14 or \(\frac{22}{7}\) for π. Round to the nearest hundredth, if necessary. (Examples 1 and 2)
Question 3.
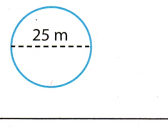
Answer:
Diameter of the circle is 25 m.
Use the formula for the circumference of the circle
C = π(d) Substitute 25 for d, and 3.14 for π.
C ≈ 3.14(25)
C ≈ 78.5
The circumference ¡s about 78.5 m
C ≈ 78.5 m.
Question 4.
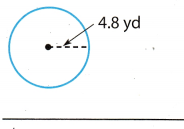
Answer:
The radius of the circle is 4.8 yd.
Use the formula for the circumference of the circle.
C = 2πr(r) Substitute 4.8 for r, and 3.14 for π.
C ≈ 2 . 3.14(4.8)
C ≈ 30.14
The circumference is about 30 yd.
Question 5.
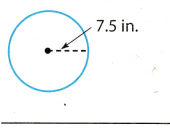
Answer:
The radius of the circle is 1.5 in.
Use the formula for the circumference of the circle.
C = 2πr(r) Substitute 7.5 for r, and 314 for π.
C ≈ 2 . 3.14(1.5)
C ≈ 47.1
The circumference is about 47 in.
C ≈ 41 in.
Question 6.
A round swimming pool has a circumference of 66 feet. Carlos wants to buy a rope to put across the diameter of the pool. The rope costs $0.45 per foot, and Carlos needs 4 feet more than the diameter of the pool. How much will Carlos pay for the rope? (Example 3)
Find the diameter.
C = πd
____ ≈ 3.14d
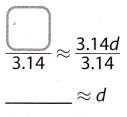
Find the cost.
Carlos needs ____ feet of rope.
_____ × $0.45 = ______
Carlos will pay ________ for the rope.
Answer:
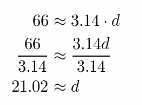
Carlos ìieeds 21,02 + 4 ≈ 25.02 feet of rope.
250.2 × $0.45 ≈ $11.26
Carlos will pay about $11.26 for the rope.
Carlos will pay about 11.25 for the rope.
Find each missing measurement to the nearest hundredth. Use 3.14 for π. (Example 1 and 3)
Question 7.
r = ___
d = ____
C = π yd
Answer:

r = \(\frac{C}{2 \cdot \pi \cdot y}\)
Question 8.
r ≈ ____
d ≈ _____
C = 78.8 ft
Answer:
C = π(d)
Substitute 78.8 for C, and 3.14 for π
78.8 ≈ 3.14(d) Divide both sides by 3.14.
\(\frac{78.8}{3.14}\) ≈ \(\frac{3.14}{3.14}(d)\)
25.09 ≈ d
d ≈ 25.09
Since the diameter of the circle is double the radius, the radius will be half of the diameter
r = d ÷ 2 Substitute 25.09 for d.
r = 25.09 ÷ 2
r = 12.54
d ≈ 25.09, r = 12.54
Question 9.
r ≈ ____
d ≈ 3.4 in.
C = ____
Answer:
Use the formula for the circumference.
C = π(d)
Substitute 3.4 for d, and 3.14 for π.
C ≈ 3.14(3.4)
C ≈ 10.68
Since the diameter of the circle is double the radius, the radius will be half of the diameter.
r = d ÷ 2 Substitute 3.4 for d.
r = (3.4) ÷ 2
r = 1.7
C ≈ 10.68 in., r = 1.7 in.
Essential Question Check-In
Question 10.
Norah knows that the diameter of a circle ¡s 13 meters. How would you tell her to find the circumference?
Answer:
Use the formula for the circumference of the circle, where d represents the diameter of the circle.
C = π(d) Supstitute 13 for d, and 3.14 for π.
C ≈ 3.14(13)
C ≈ 40.82
The circumference is about 40 m.
C ≈ 40.82 m
Texas Go Math Grade 7 Lesson 9.2 Independent Practice Answer Key
Find the circumference of each circle. Use 3.14 or \(\frac{22}{7}\) for π. Round to the nearest hundredth, if necessary.
Question 11.

Answer:
Diameter of the circle is 5.9 ft
Use the formula for the circumference of the circle.
C = π(d) Substitute 5.9 for d, and 3.14 for π.
C ≈ 3.14(5.9)
C ≈ 18.53
The circumference is about 18.53 ft.
C ≈ 18.53 ft
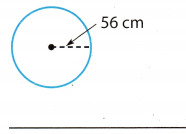
Question 12.
Answer:
The radius of the circle is 56 cm.
Use the formula for the circumference of the circle.
C = 2πr(r) Substitute 56 for r, and \(\frac{22}{7}\) for π.
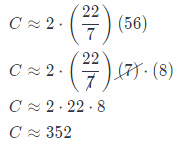
The circumference is about 352 cm.
C ≈ 352 cm
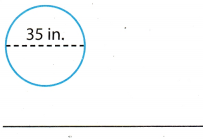
Question 13.
Answer:
The diameter of the circle is 35 in.
Use the formula for the circumference of the circle.
C = π(d) Substitute 35 for d, and \(\frac{22}{7}\) for π.
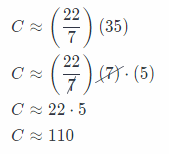
The circumference is about 110 in.
C ≈ 110 in
Question 14.
In Exercises 11—13, for which problems did you \(\frac{22}{7}\) use for π? Explain your choice.
Answer:
We use the fraction \(\frac{22}{7}\) in exercises 12 and 13 because the radius and the diameter in both exercises are divisible by 7, so we can shorten 7 from the fraction \(\frac{22}{7}\).
Question 15.
A circular fountain has a radius of 9.4 feet. Find its diameter and circumference to the nearest hundredth.
Answer:
Use the formula for the circumference.
C = 2πr
Substitute 9.4 for r, and 3.14 for π
C ≈ 2 . 3.14(9.4)
C ≈ 59.03
The diameter of the circle is double the radius
d = 2 . r Substitute 9.4 for r.
d = 2 . 9.4
d = 18.8
C ≈ 59.03 ft, d = 18.8 ft
Question 16.
Find the radius and circumference of a CD with a diamèter of 4.75 inches.
Answer:
Use the formula for the circumference.
C = π(d)
Substitute 4.75 for d, and 3.14 for π.
C ≈ 3.14(4.75)
C ≈ 14.91
Since the diameter of the circle is double the radius, the radius will be half of the diameter.
r = d ÷ 2 Substitute 4.75 for d.
r = (4.75) ÷ 2
r = 2.37
ResuLt
C ≈ 14.91 in., r = 2.37 in.
Question 17.
A dartboard has a diameter of 18 inches. What is its radius and circumference?
Answer:
Use the formula for the circumference.
C = π(d)
Substitute 18 for d, and 3.14 for π.
C ≈ 3.14(18)
C ≈ 56.52
Since the diameter of the circle is double the radius, the radius will be half of the diameter.
r = d ÷ 2 Substitute 18 for d.
r = (18) ÷ 2
r = 9
C ≈ 56.52 in., r = 9 in.
Question 18.
Multistep Randy’s circular garden has a radius of 1.5 feet. He wants to enclose the garden with edging that costs $0.75 per foot. About how much will the edging cost? Explain.
Answer:
First, we have to find the circumference of the garden.
C = 2πr(r) Substitute 1.5 for r, and 3.14 for π.
C ≈ 2.3.14(1.5)
C ≈ 9.42
The circumference of the garden is about 9.42 ft, and one foot of the edging costs $0.73. so we have to multiply the circumference with $0.75 to find how much will the edging cost.
9.12 . $0.75 ≈ $7.06
The edging will cost about $7.06.
Question 19.
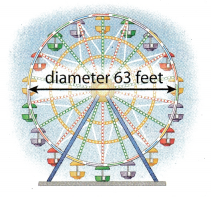
Represent Real-World Problems The Ferris wheel shown makes 12 revolutions per ride. How far would someone travel during one ride?
________
Answer:
The diameter of the wheel is 63 feet, and we have to find the circumference of the wheel, which will represents
one revolution.
C = π(d) Substitute 63 for d, and 3.14 for π.
C ≈ 3.14(63)
C ≈ 197.82
The circumference is about 197.82 ft.
The wheel makes 12 revolutions per ride, so we have to multiply the circumference with 12 to get how far
someone wouLd traveL during the one ride.
12 . 197.82 ≈ 2, 373.84 ft.
2,373.84 ft
Question 20.
The diameter of a bicycle wheel is 2 feet. About how many revolutions does the wheel make to travel 2 kilometers? Explain.
Hint: 1 km 3,280 ft
Answer:
d = 2feet
1km = 3280 feet
One revolution would be the circumference of the wheel.
Use the formula for the circumference of the circle
C = π(d) Substitute 2 for d, and 3.14 for π
C ≈ 3.14(2)
C ≈ 7.28
The circumference of the wheel is about 7.28 feet
We said that the one revolution is the circumference of the wheel so we have to find how many circumference will be 2 km.
First we have to convert 2 km to feet
1 km = 3,280 ft
2 km = 2 . 3280 ft
2km = 6,560 ft
The equation for finding how many revolutions wheel makes to travel 2 km, where x represents the number of
revolutions, is

The wheel makes about 901 revolutions to travel 2 km.
About 901 revolutions
Question 21.
Multistep A map of a public park shows a circular pond. There ¡s a bridge along a diameter of the pond that is 0.25 mi long. You walk across the bridge, while your friend walks halfway around the pond to meet you at the other side of the bridge. How much farther does your friend walk?
Answer:
The diameter of the pond is 0.25 mi long.
Use the formula for the circumference of the circle to find the circumference of the pond.
C = π(d) Substitute 0.25 for d, and 3.14 for π.
C ≈ 3.14(0.25)
C ≈ 0.78
The circumference of the pond is about 0.78 mi.
My friend walks halfway around the pond, so he walks the half circumference.
C ÷ 2 ≈ \(\frac{0.78}{2}\)
≈ 0.39
My friend walks about 0.39 mi and I walk 0.25 mi, so he walks about 0.39mi – 0.25mi = 0.14 mi farther than me.
About 0.14 mi.
Question 22.
Architecture The Capitol Rotunda connects the House and the Senate sides of the U.S. Capitol. Complete the table. Round your answers to the nearest foot.
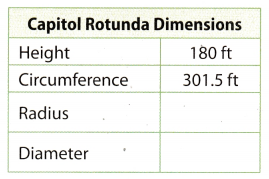
Answer:
Use the formula for the circumference.
C = 2π(r) Substitute 301.5 for C, and 3.14 for π.
301.5 ≈ 2 . 3.14(r)
301.5 ≈ 6.28(r) Divide both sides by 6.28.
\(\frac{301.5}{6.28}\) ≈ \(\frac{6.28}{6.28}(r)\)
48.01 ≈ r
r ≈ 48.01
Diameter is twice the radius, hence
d = 2 . r 2 . 48.01 ≈ 96.02
r ≈ 48.01 ft d ≈ 96.02 ft
Focus On Higher Order Thinking
Question 23.
Multistep A museum groundskeeper is creating a semicircular statuary garden with a diameter of 30 feet. There will be a fence around the garden. The fencing costs $9.25 per linear foot. About how much will the fencing cost altogether?
Answer:
The diameter of the garden is 30 feet.
To find how much will the fencing cost, first we have to find the circumference
of the garden, and then to multiply it by the price of a fence per foot($9.25).
Use the formula for the circumference of the circle.
C = π(d) Substitute .30 for d, and 3.14 for π.
C ≈ 3.14(30)
C ≈ 94.2
The circumference of the garden is about 94.2 feet.
The cost of the fencing = C . $9.25 ≈ 94.2 . $9.25 ≈ $871.35
About $871.35
Question 24.
Critical Thinking Sam is placing rope lights around the edge of a circular patio with a diameter of 18 feet. The lights come in lengths of 54 inches. How many strands of lights does he need to surround the patio edge?
Answer:
The diameter of the patio is 18 feet
First, we have to find the circumference of the patio.
Use the formula for the circumference of the circle.
C = π(d) Substitute 18 for d, and 3.14 for π.
C ≈ 3.14(18)
C ≈ 56.52
The circumference of the patio is about 56.52 feet
Convert the circumference from feet to inches, because the length of the lights is in inches
1 foot = 12 inches
C ≈ 56.52feet . 12 inches ≈ 678.24 inches
To find now many strands of lights Sam needs, we have to divide the circumference of the patio by the length of one strand. One strand is 54 inches Long.
C ÷ 54in. ≈ 678.24in. ÷ 54in. ≈ 12.56
Sam needs about 12.56 strands of lights.
Question 25.
Represent Real-World Problems A circular path 2 feet wide has an inner diameter of 150 feet. How much farther is it around the outer edge of the path than around the inner edge?
Answer:
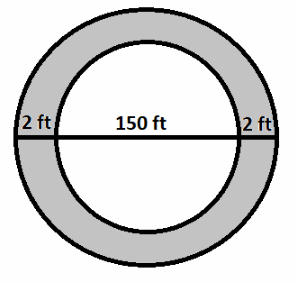
First we find the circumference of the inner circle with the diameter of 150 ft, which will represents the inner edge.
The outer edge is the circumference of the circle which diameter we get as the sum of the diameter of the inner
circle and two times path width.
Let d1 be the diameter of the inner circle and d2 the diameter of the outer circle.
d2 = d1 + 2 . 2 feet Subtract 150 for d_1.
d2 = 150 feet + 4 feet
d2 = 154 feet
Let C1 be the circumference of the inner circle and C2 the circumference of the outer circle.
Use the formula for the circumference of the circle.
C1 = π(d1) Substitute 150 for d_1, and 3.14 for π.
C1 ≈ 3.14(150)
C1 ≈ 471
The circumference of the inner circle is about 471 feet
C2 = π(d2) Substitute 154 for d_2 and 3.14 for π.
C2 ≈ 3.14(154)
C2 ≈ 483.56
The circumference of the inner circle is about 483.56 feet.
The difference between these two circumferences represents how much farther is it around the outer egde, then around the inner edge of the path.
C2 – C1 = 483.56 – 471 = 12.56
Outer edge is 12.56, feet farther than the inner edge.
Outer edge is 12.56, feet farther than the inner edge
Question 26.
Critique Reasoning A gear on a bicycle has the shape of a circle. One gear has a diameter of 4 inches, and a smaller one has a diameter of 2 inches Justin says that the circumference of the larger gear is 2 inches more than the circumference of the smaller gear. Do you agree? Explain your answer.
Answer:
I do not agree. The circumference doesn’t depends only on the diameter, but also on the number of π. Proof.
Let d1 be the diameter of the larger gear and d2 the diameter of the smaller gear.
d1 = 4 inches
d2 = 2 inches
Let C1 be the circumference of the larger gear and C2 the circumference of the smaller gear.
Use the formula for the circumference of the circle.
C1 = π(d1) Substitute 4 for d_1, and 3.14 for π.
C1 ≈ 3.14(4)
C1 ≈ 12.56
The circumference of the larger gear is about 12.56 inches.
C2 = π(d2) Substitute 2 for d_2, and 3.14 for π.
C2 ≈ 3.14(2)
C2 ≈ 6.28
The circumference of the smaller gear is about 6.28 inches.
C1 – C2 = 12.56 – 6.28 = 6.28 inches
The difference between these two circumferences is greater than 2 inches, actually, the difference is (2 inches × π).
The difference between these two circumferences is greater than 2 inches.
Question 27.
Persevere In Problem Solving Consider two circular swimming pools. Pool A has a radius of 12 feet, and Pool B has a diameter of 7.5 meters. Which pool has a greater circumference? How much greater? Justify your
answers.
Answer:
In order to compare these two pools, both measuring units must be the same.
1 foot = 0.3048 m
Let r1 be the radius of the Pool A and r2 the radius of the Pool B.
r1 = 12 . 0.3048 m = 3.66 m
r2 = 7.5 m
Let C1 be the circumference of the Pool A and C2 the circumference of the Pool B.
Use the formula for the circumference of the circle.
C1 = π(r1) Substitute 3.66 for r_1, and 3.14 for π.
C1 ≈ 3.14(3.66)
C1 ≈ 11.5
The circumference of the Pool A is about 11.5 m
C2 = π(r2) Substitute 3.66 for r_2, and 3.14 for π.
C2 ≈ 3.14(7.5)
C2 ≈ 23.55
The circumference of the Pool B is about 23.55 m.
Hence,
C1 < C2
The difference between these two circumferences represents how much greater Pool. B is than Pool. A.
C2 – C1 ≈ 23.55 – 11.5 ≈ 12.05
The Pool B is greater than Pool A for about 12.05 m.
C1 < C2