Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 6.4 Answer Key Using Technology to Conduct a Simulation.
Texas Go Math Grade 7 Lesson 6.4 Answer Key Using Technology to Conduct a Simulation
Your Turn
Question 1.
An elephant has a 50% chance of giving birth to either a male or to a female calf. Use a simulation to find the experimental probability that the elephant gives birth to 3 male calves before having a female calf. (Hint: Use 0s and 1s. Let 0 represent a male calf, and 1 represent a female calf. Generate random numbers until you get a 1.)
Answer:
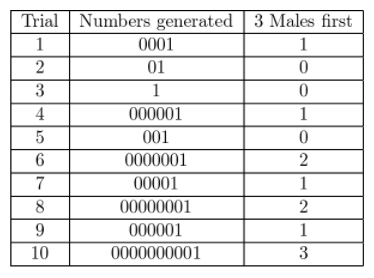
The probability that the elephant gives a birth to three male calves before having a fimale calf is \(\frac{7}{10}\).
Question 2.
Matt guesses the answers on a quiz with 5 true-false questions. The probability of guessing a correct answer on each question is 50%. Use a simulation to find an experimental probability that he gets at least 2 questions right. (Hint: Use 0s and is. Let 0s represent incorrect answers, and 1s represent correct answers. Perform 10 trials, generating 5 random numbers in each, and count the number of 1s.)
Answer:
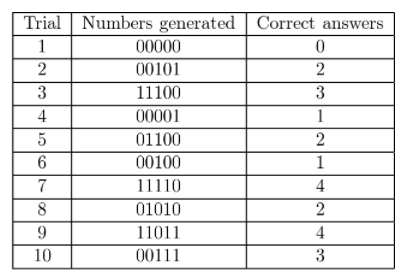
The probability to get at least 2 question right is \(\frac{7}{10}\).
Texas Go Math Grade 7 Lesson 6.4 Guided Practice Answer Key
There is a 30% chance that T’Shana’s county will have a drought during any given year. She performs a simulation to find the experimental probability of a drought in at least 1 of the next 4 years. (Examples 1 and 2)
Question 1.
T’Shana’s model involves the whole numbers from 1 to 10. Complete the description of her model.
Let the numbers 1 to 3 represent _____________ and the numbers 4 to 10 represent _____________
Perform multiple trials, generating _______ random numbers each time.
Answer:
Let the numbers 1 to 3 represent that will be drought during any given year, and the numbers 4 to 10 represent that will not have drought during any year.
Perform multiple trials, generating 4 random numbers each time.
Question 2.
Suppose T’Shana used the model described in Exercise 1 and got the results shown in the table. Complete the table.
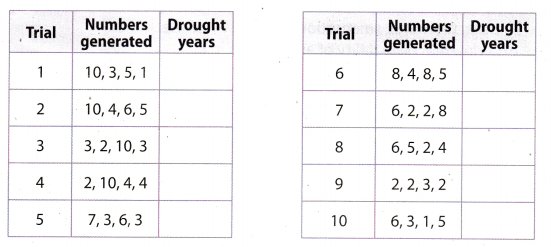
Answer:
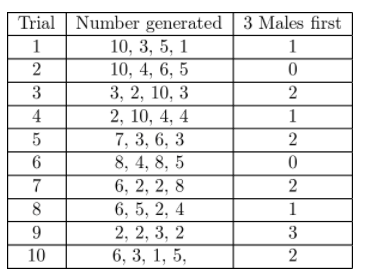
The probability that there will be a drought in the country at least 1 of the next 4 years is \(\frac{8}{10}\).
Question 3.
According to the simulation, what is the experimental probability that there will be a drought in the county in at least 1 of the next 4 years?
Answer:
The probability that there will be a drought in the country at least 1 of the next 4 years is \(\frac{8}{10}\).
Essential Question Check-In
Question 4.
You want to generate random numbers to simulate an event with a 75% chance of occurring. Describe a model you could use.
Answer:
The probability of some event is = \(\frac{75}{100}\) = \(\frac{3}{4}\).
We can use number 1, 2, 3 which represent that the chosen event is happen and 4 that is not.
Generating a random number in every trial until you get 1 or 2 or 3.
Texas Go Math Grade 7 Lesson 6.4 Independent Practice Answer Key
Every contestant on a game show has a 40% chance of winning. In the simulation below, the numbers 1-4 represent a winner, and the numbers 5-10 represent a non winner. Numbers were generated until one that represented a winner was produced.

Question 5.
In how many of the trials did it take exactly 4 contestants to get a winner?
Answer:
Only in one. In the eighth trial it was taken exactly 4 contestants to get a winner.
Question 6.
Based on the simulation, what is the experimental probability that it will take exactly 4 contestants to get a winner?
Answer:
The probability to take exactly 4 contestants to get a winner is \(\frac{1}{10}\).
Over a 100-year period, the probability that a hurricane struck Rob’s city in any given year was 20%. Rob performed a simulation to find an experimental probability that a hurricane would strike the city in at least 4 of the next 10 years. In Rob’s simulation, 1 represents a year with a hurricane.
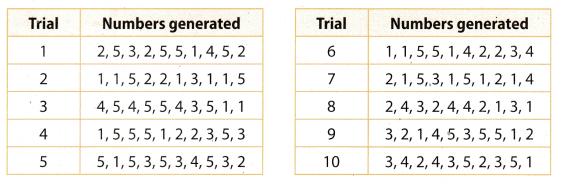
Question 7.
According to Rob’s simulation, what was the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years?
Answer:
The experimental probability that a hurricane would strike the city in at last 4 of the next 10 years is \(\frac{2}{10}\) = \(\frac{1}{5}\).
Question 8.
Analyze Relationships Suppose that over the 10 years following Rob’s simulation, there was actually 1 year in which a hurricane struck. How did this compare to the results of Rob’s simulation?
Answer:
The probability that over the 10 years, where was 1 year in which hurricane struck is \(\frac{3}{10}\).
How is the experimental probability of Rob’s simulation \(\frac{1}{5}\), the probability that over the 10 years, where was 1 year in. which hurricane struck is greater.
Question 9.
Communicate Mathematical Ideas You generate three random whole numbers from 1 to 10. Do you think that it is unlikely or even impossible that all of the numbers could be 10? Explain?
Answer:
The probability that in three generated numbers all of three is 10 is:
P (in each is 10) = \(\frac{1}{1000}\)
Because we have 10 possibilities for first ∙ 10 possibilities for second ∙ 10 possibilities for third = 1000, but only one that all of three are 10.
Question 10.
Erika collects baseball cards, and 60% of the packs contain a player from her favorite team. Use a simulation to find an experimental probability that she has to buy exactly 2 packs before she gets a player from her favorite team.
Answer:
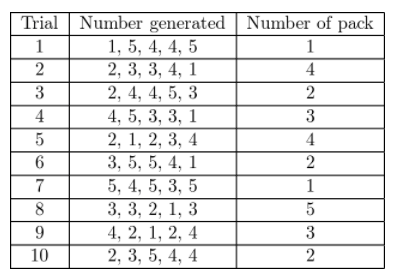
The probability that she has to buy exactly 2 packs before she gets a player from fer favorite time is \(\frac{3}{10}\).
H.O.T. Focus on Higher Order Thinking
Question 11.
Represent Real-World Problems When Kate plays basketball, she usually makes 37.5% of her shots. Describe a simulation that you could use to find the experimental probability that she makes at least 3 of her next 10 shots.
Answer:
The probability that Kate makes a shot is \(\frac{3}{8}\).
Let 1, 2 and 3 represent that she makes a shot and 4, 5, 6, 7 and 8 that not. Generate 5 numbers in each of 10 trials and find a experimental probability that she makes at least 3 of the 10 shots.
Question 12.
Justify Reasoning George and Susannah used a simulation to simulate the flipping of 8 coins 50 times. In all of the trials, at least 5 heads came up. What can you say about their simulation? Explain.
Answer:
The experimental probability that Susannah and George flips at least 5 heads ¡n every trial is greater than flipping a tails, because in every attempt, if that flip at least 5 heads, there are 3 or less possibilities for the tails.