Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 5.4 Answer Key Making Predictions with Experimental Probability.
Texas Go Math Grade 7 Lesson 5.4 Answer Key Making Predictions with Experimental Probability
Your Turn
Question 1.
A car rental company sells accident insurance to 24% of its customers. Out of 550 customers, about how many customers are predicted to purchase insurance?.
Answer:
Find 24% of 550.
Write 24% as a fraction. The percent equation will be
x = \(\frac{24}{1000}\) ∙ 550 Write fraction as decimal.
= 0.24 ∙ 550 Multiply.
= 132
About 132 customers of 550 are predicted to purchase insurance.
Example 2
A doctor’s office records data and concludes that, on average, 11% of patients call to reschedule their appointments per week. The office manager predicts that 23 appointments will be rescheduled out of the 240 total appointments during next week. Explain whether the prediction is reasonable.
Method 1: Use a proportion.

Method 2: Use a percent equation.
0.11 ∙ 240 = x Find 11% of 240.
26.4 = x Solve for x
The prediction of 23 is reasonable but a little low, because 23 is a little less than 26.4.
Reflect
Question 2.
Does 26.4 make sense for the number of patients? Explain.
Answer:
36.4 is the solution of the equation for finding the average number of patients that would call to reschedule.
But, we can not divide people, so we need to round the solution of the equation to a smaller whole number, hence, about 26 people would call to reschedule.
Your Turn
Question 3.
In emails to monthly readers of a newsletter 3% of the emails come back undelivered. The editor predicts that if he sends out 12,372 emails, he will receive 437 notices for undelivered email. Do you agree with his prediction? Explain.
Answer:
Find 3% of 12, 372.
Write 3% as a fraction. The percent equation will be
x = \(\frac{3}{100}\) ∙ 12, 372 Write fraction as decimal.
= 0.03 ∙ 12. 372 Multiply.
= 371.16
We need to round the solution of the equation to a smaller whole number, hence, about 371 of 12, 372 emails are predicted to come back undelivered.
The prediction of 437 isn’t reasonable, because 371 is way Less than 437.
Question 4.
On average, 24% of customers who buy shoes in a particular store buy two or more pairs. One weekend, 350 customers purchased shoes. How many can be predicted to buy two or more pairs? If 107 customers buy more than two pairs, did more customers than normal buy two or more pairs?
Answer:
Find 24% of 350.
Write 24% as a fraction. The percent equation will. be
x = \(\frac{24}{100}\) ∙ 350 Write fraction as decimal
= 0.24 ∙ 350 Multiply.
= 84
84 is average number of customers that buy two or more pairs of shoes.
If 107 customers buy more than two pairs of shoes, this is more than normal customers who buy two or more pairs, because 107 > 84.
Texas Go Math Grade 7 Lesson 5.4 Guided Practice Answer Key
Question 1.
A baseball player reaches first base 30% of the times he is at bat. Out of 50 times at bat, about how many times will the player reach first base? (Example 1)
Answer:
Find 30% of 50.
Write 30% as a fraction. The percent equation will be
x = \(\frac{30}{100}\) ∙ 50 Write fraction as decimal.
= 0.3 ∙ 50 Multiply
=15
About 15 times will the player reach first base.
Question 2.
The experimental probability that it will rain on any given day in Houston, Texas, is about 15%. Out of 365 days, about how many days can residents predict rain? (Example 1)
Answer:
Find 15% of 365.
Write 15% as a fraction. The percent equation will be
x = \(\frac{15}{100}\) ∙ 365 Write fraction as decimal.
= 0.15 ∙ 365 Multiply.
= 54.75
We need to round the solution of the equation to a smaller whole number, hence, about 54 of 365 days residents predict rain in Houston in Texas.
Question 3.
A catalog store has 6% of its orders returned for a refund. The owner predicts that a new candle will have 812 returns out of the 16,824 sold. Do you agree with this prediction? Explain. (Example 2)
Answer:
Find 6% of 16,824.
Write 6% as a fraction. The percent equation will be
x = \(\frac{6}{100}\) ∙ 824 Write fraction as decimal
= 0.06 ∙ 16, 824 Multiply.
= 1009.44
We need to round the solution of the equation to a smaller whole number, hence, about 1009 of 16,824 orders will return for a refund.
The prediction of 812 is reasonable, but a lot low, because 1009 is a lot greater than 812.
Question 4.
On a toy assembly line, 3% of the toys are found to be defective. The quality control officer predicts that 872 toys will be found defective out of 24,850 toys made. Do you agree with this prediction? Explain. (Example 2)
Answer:
Find 3% of 24, 850.
Write 3% as a fraction. The percent equation will be
x = \(\frac{3}{100}\) ∙ 24,850 Write fraction as decimal
= 0.03 ∙ 24. 850 Multiply.
= 745.5
We need to round the solution of the equation to a smaller whole number, hence, about 745 of 24, 850 toys will be defective.
The prediction of 872 isn’t reasonable, because 872 is a lot greater than predicted number of defective toys.
Question 5.
A light-rail service claims to be on time 98% of the time. If Jeanette takes the light-rail 40 times one month, how many times can she predict she will be on time? Is the light-rail’s claim accurate if she is late 6 times? (Example 3)
Answer:
Find 98% of 40.
Write 98% as a fraction. The percent equation will be
x = \(\frac{98}{100}\) ∙ 40 Write fraction as decimal
= 0.98 ∙ 40 Multiply.
= 39.2
We need to round the solution of the equation to a smaller whole number, hence, about 39 of 40 times she will be on time.
Only once she will be late.
Question 6.
On average, a college claims to accept 18% of its applicants. If the college has 5,000 applicants, predict how many will be accepted. If 885 applicants are accepted, is the college’s claim accurate? (Example 3)
Answer:
Find 18% of 5000.
Write 18% as a fraction. The percent equation will be
x = \(\frac{18}{100}\) ∙ 5000 Write fraction as decimal.
= 0.18 ∙ 5000 Multiply.
= 900
About 900 of 5000 applicants will be accepted.
The claim is correct because 885 is less than the number of predicted applicants.
Essential Question Check-In
Question 7.
How do you make predictions using experimental probability?
Answer:
We can equalize the probability with a fraction that has an unknown number in numerator, white in denominator is a number of times how many times the experiment was repeated.
Texas Go Math Grade 7 Lesson 5.4 Independent Practice Answer Key
The table shows the number of students in a middle school at the beginning of the year and the percentage that can be expected to move out of the area by the end of the year.
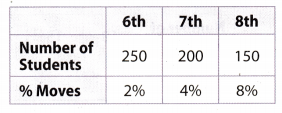
Question 8.
How many 7th grade students are expected to move by the end of the year? If 12 students actually moved, did more or fewer 7th grade students move than expected? Justify your answer.
Answer:
Find 4% of 200.
Write 4% as a fraction. The percent equation will be
x = \(\frac{4}{100}\) ∙ 200 Write fraction as decimal.
= 0.04 ∙ 200 Multiply.
=8
About 8 7th grade students wilt move by the end of the year.
12 > 7, hence, more than predicted number of 7th grade students moved by the end of the year.
Question 9.
Critique Reasoning The middle school will lose some of its funding if 50 or more students move away in any year. The principal claims he only loses about 30 students a year. Do the values in the table support his claim? Explain.
Answer:
Find how much students of all grades expected to move by the end of the year.
6th grade
Find 2% of 250.
Write 2% as a fraction. The percent equation will be
x1 = \(\frac{2}{100}\) ∙ 250 Write fraction as decimal.
= 0.02 ∙ 250 Multiply.
= 5
About 5 6th grade students will move by the end of the year.
7th grade
Find 4% of 200.
Write 4% as a fraction. The percent equation will be
x2 = \(\frac{4}{100}\) ∙ 200 Write fraction as decimal.
= 0.04 ∙ 200 Multiply.
= 8
About 8 7th grade students will move by the end of the year.
8th grade
Find 8% of 150.
Write 8% as a fraction. The percent equation will be
x3 = \(\frac{8}{100}\) ∙ 150 Write fraction as decimal.
= 0.08 ∙ 150 Multiply.
= 12
About 12 8th grade students will move by the end of the year.
x1 + x2 + x3 = 5 + 8 + 12 = 25
About 25 students of all grades will move by the end of the year.
Principal claim is correct, because 30 students is less than the predicted number of student who will move by the end of the year.
Question 10.
Represent Real-World Problems An airline knows that, on average, the probability that a passenger will not show up for a flight is 6%. If an airplane is fully booked and holds 300 passengers, how many seats are expected to be empty? If the airline overbooked the flight by 10 passengers, about how many passengers are expected to show up for the flight? Justify your answer.
Answer:
Find 6% of 300.
Write 6% as a fraction. The percent equation will be
x = \(\frac{6}{100}\) ∙ 300 Write fraction as decimal
= 0.06 ∙ 300 Multiply.
=18
About 18 of 300 passengers will not show up for a flight if airplane is fully booked, hence, about 18 seats will be empty.
If airline overbooked the flight by 10 passengers, we have to add 10 to 300 and then find 4% of that sum.
Write 6% as a fraction. The percent equation will be
x = \(\frac{6}{100}\) ∙ 310 Write fraction as decimal.
= 0.06 ∙ 310 Multiply.
= 18.6
We need to round the solution of the equation to a smaller whole number, hence, about 18 of 310 passengers will not show up for a flight.
Hence, about 310 – 18 = 292 passengers will show up for the flight.
Question 11.
Draw Conclusions In a doctor’s office, an average of 94% of the clients pay on the day of the appointment. If the office has 600 clients per month, how many are expected not to pay on the day of the appointment? If 40 clients do not pay on the day of their appointment in a month, did more or fewer than the average not pay?
Answer:
Find 94% of 600.
Write 94% as a fraction. The percent equation will be
x = \(\frac{94}{100}\) ∙ 600 Write fraction as decimal.
= 0.94 ∙ 600 Multiply.
= 564
About 564 of 600 clients will. pay on the day of the appointment in a month.
Hence, about 600 – 564 = 36 clients who will not pay on the day of the appointment.
40 clients is more than expected number of clients who don’t pay on the day of their appointment in a month.
Question 12.
Counterexamples The soccer coach claimed that, on average, only 80% of the team comes to practice each day. The table shows the number of students that came to practice for 8 days. If the team has 20 members, how many team members should come to practice to uphold the coach’s claim? Was the coach’s claim accurate? Explain your reasoning.

Answer:
Find 80% of 20.
Write 80% as a fraction. The percent equation will be
x = \(\frac{20}{100}\) ∙ 80 Write fraction as decimal.
= 0.2 ∙ 80 Multiply.
= 16
About 16 students od 20 should to practice each day to uphold the coach’s claim.
From the table, we have to find the average number of students that comes to practice each day, and compare it with coach’s claim.
To find the average number of students that comes to practice each day, we have to sum the number of students that comes every day, and then divide that sum with the number of days.
x = \(\frac{18+15+18+17+17+19+20+20}{8}=\frac{144}{8}\) = 18
About 18 students comes to practice each day, hence, coach’s claim is correct
Question 13.
What’s the Error? Ronnie misses the school bus 1 out of every 30 school days. He sets up the proportion \(\frac{1}{30}\) = \(\frac{180}{x}\) to predict how many days he will miss the bus in the 180-day school year. What is Ronnie’s error?
Answer:
He writes 1 of 30 is 180 out of how many, instead of 1 of 30 is how many out of 180, because he wants to predict how many days of 180 he will miss the bus.
The right proportion is
\(\frac{1}{30}\) = \(\frac{x}{180}\)
H.O.T. Focus on Higher Order Thinking
Question 14.
Persevere in Problem Solving A gas pump machine rejects 12% of credit card transactions. If this is twice the normal rejection rate for a normal gas pump, how many out of 500 credit card transactions would a normal gas pump machine reject?
Answer:
Find 12% of 500.
Write 12% as a fraction. The percent equation will be
x = \(\frac{12}{100}\) ∙ 500 Write fraction as decimal
= 0.12 ∙ 500 Multiply.
= 60
About 60 of 500 credit card transactions will, be rejected by a gas pump machine.
Since 60 is twise the normal rejections number for a normal gas pump, normal gas pump machine wilt reject half of 60, hence, 30 credit card transactions.
Question 15.
Make Predictions An airline’s weekly flight data showed a 98% probability of being on time. If this airline has 15,000 flights in a year, how many flights would you predict to arrive on time? Explain whether you can use the data to predict whether a specific flight with this airline will be on time.
Answer:
P (flight arrive on time) = \(\frac{98}{100}\) = \(\frac{49}{50}\)
Use proportion.
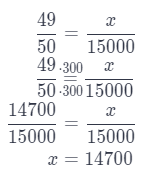
In order to determine the probability of a particular flight, we need to know how many of the 15,000 flights arrived in time.
Question 16.
Draw Conclusions An average response rate for a marketing letter is 4%, meaning that 4% of the people who receive the letter respond to it. A company writes a new type of marketing letter, sends out 2,400 of them, and gets 65 responses. Explain whether the new type of letter would be considered to be a success.
Answer:
Find 4% of 2400.
Write 4% as a fraction. The percent equation will be
x = \(\frac{4}{100}\) ∙ 2400 Write fraction as decimal.
= 0.04 ∙ 2400 Multiply.
= 96
About 96 of 2400 letters get responses.
If company sends out 2400 of new type marketing Letters and gets 65 responses, the new type of marketing letters aren’t successful because the average number of the letters with responses is 96, and 65 is way less than 96.