Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 4.1 Answer Key Similar Shapes and Proportions.
Texas Go Math Grade 7 Lesson 4.1 Answer Key Similar Shapes and Proportions
Texas Go Math Grade 7 Lesson 4.1 Explore Activity Answer Key
Similar Shapes and Proportions
Similar shapes have the same shape but not necessarily the same size. You can use square tiles to model similar figures.
A rectangle made of square tiles measures 5 tiles long and 2 tiles wide. Find the length of a similar rectangle that measures 6 tiles wide.
STEP 1: Using the square tiles, make a rectangle 5 tiles long and 2 tiles wide.
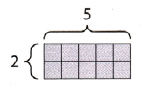
STEP 2: Add tiles to increase the width of the rectangle to 6 tiles.
There are now _____ sets of the original _____ tiles along the width of the rectangle because _____ × _____ = 6.
The width of the rectangle is _____ times the width of the original rectangle.
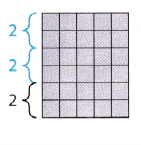
STEP 3: Add tiles to also increase the length of the rectangle.
The width of the new rectangle is _____ times the width of the original. To keep the lengths of the sides
proportional, the length must also be _____ times the length of the original. The length of the similar rectangle is _____ × ____ = 15.
The length of the similar rectangle is ________ tiles.

Reflect
Question 1.
Justify Reasoning If one dimension is changed, why does the other dimension have to change to create a similar figure?
Answer:
The other dimension has to change because the ratio between dimensions of the similar figure has to remain the same
Your Turn
Explain whether the triangles are similar.
Question 2.

Answer:
The corresponding angles of a triangle do not have equal measures. Thus, the triangles are not similar.
Question 3.
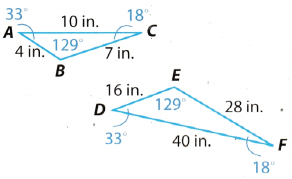
Answer:
Check that the corresponding angles of the triangle have equal measures.
m∠A = m∠D = 33°
m∠B = m∠E = 129°
m∠C = m∠F = 18°
Corresponding angles ensure that the corresponding sides will be proportional Thus, the triangles are similar
Your Turn
Explain whether the shapes are similar.
Question 4.
rectangle ABCD with sides of 7 and 5 and rectangle MNOP with sides of 21 and 15
Answer:
Let \(\overline{A B}\) = 7, \(\overline{C D}\) = 7, \(\overline{B C}\) = 5, \(\overline{A D}\) = 5
Let \(\overline{M N}\) = 21, \(\overline{O P}\) = 21, \(\overline{N O}\) = 15, \(\overline{M P}\) = 15.
AngLes are corresponding ALL are equal to 90°.
\(\overline{A B}\), \(\overline{C D}\) correspond to \(\overline{M N}\), \(\overline{O P}\) respectively.
\(\overline{B C}\), \(\overline{A D}\) correspond to \(\overline{N O}\), \(\overline{M P}\) respectively.

Since the measures of the corresponding angles are equal and the corresponding sides are proportional, the rectangles are proportional.
Question 5.
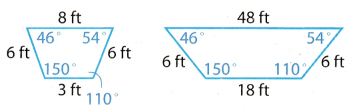
Answer:
It is obvious from the scale drawing that the corresponding angles are equal.
Now, let’s check for the sides
The shapes are not similar because the ratios between corresponding sides are not equal.
Texas Go Math Grade 7 Lesson 4.1 Guided Practice Answer Key
Question 1.
A rectangle made of square tiles measures 7 tiles long and 3 tiles wide. What is the length of a similar rectangle whose width is 9 tiles? (Explore Activity)
Answer:
Ratios between dimensions have to be preserved.
\(\frac{7}{l}\) = \(\frac{3}{9}\)
7 × 9 = 3l
3l = 63
l = 21
Length of a similar rectangle whose width is 9 tiles is 21 tiles.
Explain whether the shapes are similar. (Examples 1 and 2)
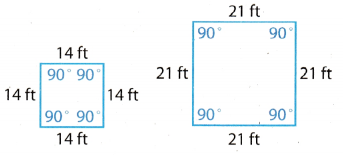
Question 2.
Answer:
We can see without looking whether sides correspond that the angles do not correspond. Thus, the triangles are not similar.
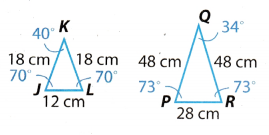
Question 3.
Answer:
The angles are corresponding.
We can see that both shapes have the same length of sides. We can conclude that both shapes are squares.
Thus, the shapes are similar.
Essential Question Check-In
Question 4.
Describe how to use ratios to determine whether two shapes are similar.
Answer:
First check if the angles are corresponding. Then, check if the ratios of corresponding sides is equal.
Texas Go Math Grade 7 Lesson 4.1 Independent Practice Answer Key
Determine if each statement is true or false. Justify your answer.
Question 5.
All squares are similar. __________
Answer:
Let’s check what does it take for a quadrangle to be a square.
- All of quadrangle’s sides must have the same length.
- All of quadrangle’s angles must be equal to 90°
Now, it is obvious that the angles are corresponding. Next, we can see that the ratios of corresponding sides are obviously equal because all 4 sides of a square are of equal length.
Thus, all squares are similar.
Question 6.
All right triangles are similar. __________
Answer:
False
A triangle needs to have one right angle to be a right triangle That does not mean the other 2 angles are corresponding. Thus, all right angles are not similar.
Art For 7-10, use the table. Assume all angle measures are equal to 90°.

Question 7.
Hugo has a small print of one of the paintings in the table. It is similar in size to the original. The print measures 11 in. × 10 in. Of which painting is this a print? Explain.
Answer:
It is a print of “The dance class” because the dimensions are corresponding
\(\frac{11}{33}\) = \(\frac{10}{30}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\)
Question 8.
A local artist painted a copy of Cezanne’s painting. It measures 88 in. × 74 in. Is the copy similar to the original? Explain.
Answer:
Check if the ratios between corresponding dimensions are equal
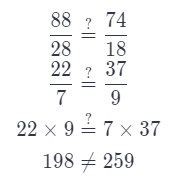
The copy is not similar to the original.
Question 9.
A company made a poster of da Vinci’s painting. The poster is 5 feet 3.5 feet wide. Is the poster similar to the original Mona Lisa? Explain.
Answer:
Check if the ratios between corresponding dimensions are equal
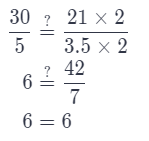
The copy is similar to the original.
Question 10.
The same company made a poster of The Blue Vase. The poster is 36 inches long and 26 inches wide. Is the poster similar to the original The Blue Vase? Explain.
Answer:
Check if the ratios between corresponding sides are equal
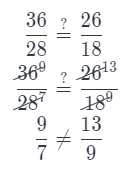
The copy is not similar to the original.
Problem Solving The figure shows a 12 ft by 15 ft garden divided into four rectangular parts, each planted with a different vegetable. Explain whether the rectangles in each pair are similar and why.
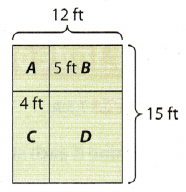
Question 11.
rectangle A and the original rectangle
Answer:
Check if the ratios between corresponding sides are equaL
OriginaL rectangLe: 12 ft. by 15 ft.
Rectangle A: 4 ft. by 5 ft.
\(\frac{12}{4}\) \(\stackrel{?}{=}\) \(\frac{15}{5}\)
3 = 3
Rectangle A and the original rectangle are similar.
Question 12.
the original rectangle and rectangle D
Answer:
Check if the ratios between corresponding sides are equal.
Original rectangle: 12 ft. by 15 ft.
Rectangle D: (12 – 4) ft. by (15 – 5) ft.
Rectangle D: 8 ft. by 10 ft.
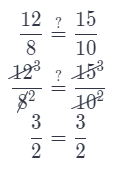
Rectangle D and the original rectangle are similar.
Question 13.
rectangle C and rectangle B
Answer:
Check if the ratios between corresponding sides are equal.
Rectangle B: 5 ft. by (12 – 4) ft.
Rectangle B: 5 ft. by 8 ft.
Rectangle C: 4 ft. by (15 – 5) ft.
Rectangle C: 4 ft. by 10 ft.
\(\frac{5}{4}\) ≠ \(\frac{8}{10}\)
Observe that the fraction on the left side is greater than 1, and the fraction on the right side is lesser that 1. We can conclude that they are not equal without further calculation.
Rectangle B and rectangle C are not similar.
H.O.T. FOCUS ON HIGHER ORDER THINKING
Question 14.
Analyze Relationships Which of these four-sided shapes are similar?

Answer:
First, compare the first and the second shape.
They both have all 4 angles equal to 90°
Now, we can check the ratios between corresponding sides.
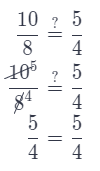
The first and the second shape are similar
Now, we can see that the first and the third shape have equal corresponding sides. Thus, the ratios between corresponding sides are equal.
But, are they similar? The answer is no Because the corresponding angles are obviously not equal.
The first and the third shape are not similar.
Now, we can just look at the angles in the second and the third shape. We can see that the corresponding angles are not equal.
The second and the third shape are not similar.
Question 15.
Communicate Mathematical Ideas Describe the two tests two polygons must pass to be proven similar.
Answer:
First test: Two polygons must have equal corresponding angles.
Second test: Two polygons must have equal ratios between their corresponding sides.
Question 16.
Make a Conjecture Using what you know of similar figures, explain whether you believe all rectangles are similar. Give an example or a counter example.
Answer:
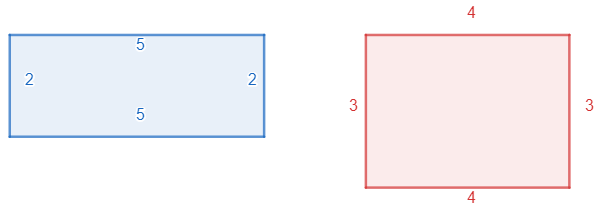
All rectangles have equal corresponding angles.
But, they do not necessarily have to have equal ratios between their corresponding angles.
Check the ratios between corresponding sides from the rectangles on the picture.
\(\frac{5}{4}\) ≠ \(\frac{2}{3}\)
We can see right away that \(\frac{5}{4}\) > 1 and \(\frac{2}{3}\) < 1. Thus, they are not equal.
We have found a counter example.