Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 2.1 Answer Key Unit Rates.
Texas Go Math Grade 7 Lesson 2.1 Answer Key Unit Rates
Texas Go Math Grade 7 Lesson 2.1 Explore Activity 1 Answer Key
Jeff hikes \(\frac{1}{2}\) mile every 15 minutes, or \(\frac{1}{4}\) hour. Lisa hikes \(\frac{1}{3}\) mile every 10 minutes, or \(\frac{1}{6}\) hour. How far do they each hike in 1 hour? 2 hours?
A. Use the bar diagram to help you determine how many miles Jeff hikes. How many \(\frac{1}{4}\)hours are in 1 hour? How far does Jeff hike in 1 hour?
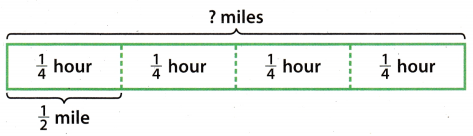
B. Complete the table for Jeff’s hike.
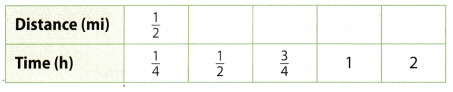
C. Complete the bar diagram to help you determine how far Lisa hikes. How many miles does she hike in 1 hour?
D. Complete the table for Lisa’s hike.

Reflect
Question 1.
How did you find Jeff’s distance for \(\frac{3}{4}\) hour?
Answer:
I multiplied how many miles he walks in \(\frac{1}{4}\) by 3.
Question 2.
Which hiker walks farther in one hour? Which is faster?
Answer:
Both walkers walk 2 miles in 1 hour. Neither of them is faster than the other.
Your Turn
Question 3.
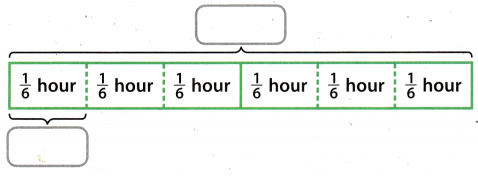
Paige mows \(\frac{1}{6}\) acre in \(\frac{1}{4}\) hour. How many acres does Paige mow per hour?
Answer:
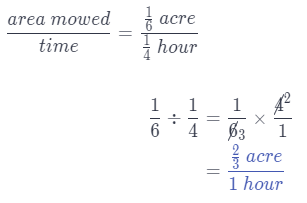
Paige mows \(\frac{2}{3}\) acre per hour.
Question 4.
Greta uses 3 ounces of pasta to make \(\frac{3}{4}\) of a serving of pasta. How many ounces of pasta are there per serving?
Answer:

Greta uses 4 ounces of pasta per serving.
Question 5.
One tank is filling at a rate of \(\frac{3}{4}\) gallon per \(\frac{2}{3}\) minute. A second tank is filling at a rate of \(\frac{5}{8}\) gallon per \(\frac{1}{2}\) minute. Which tank is filling faster?
Answer:
First find rate in gallons per minute at which each tank is filling.
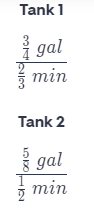
To find the unit rates, first rewrite the fractions.
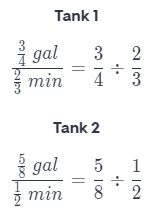
To divide, multiply with the reciprocal.

Thus, Tank 2 is filling faster.
Texas Go Math Grade 7 Lesson 2.1 Guided Practice Answer Key
Question 1.
Brandon enters bike races. He bikes 8\(\frac{1}{2}\) miles every \(\frac{1}{2}\) hour. Complete the table to find how far Brandon bikes for each time interval. (Explore Activity)

Answer:

First, notice that every step of time is half an hour longer.
Thus. simply add the distance lie cross in half an hour to every successive distance box.
8\(\frac{1}{2}\) + 8\(\frac{1}{2}\) = 17
17 + 8\(\frac{1}{2}\) = 25\(\frac{1}{2}\)
25\(\frac{1}{2}\) + 8\(\frac{1}{2}\) = 34
34 + 8\(\frac{1}{2}\) = 42\(\frac{1}{2}\)
Find each unit rate. (Example 1)
Question 2.
Julio walks 3\(\frac{1}{2}\) miles in 1\(\frac{1}{4}\) hours.
Answer:
Determine the units of the rate.
The rate is distance in mites per time in hours.
Find Julio’s rate of walking in distance walked per time.

Julio walks 2\(\frac{4}{5}\) miles per hour.
Question 3.
Kenny reads \(\frac{5}{8}\) page in \(\frac{2}{3}\) minute.
Answer:
Determine the units of the rate.
The rate is pages read per time in minutes.
Find Kenny’s rate of reading in pages read per time.

Kenny reads \(\frac{15}{16}\) pages per minute.
Question 4.
A garden snail moves \(\frac{1}{6}\) foot in \(\frac{1}{3}\) hour.
Answer:
Determine the units of the rate.
The rate is distance in feet per time in hours.
Find snails rate of moving in distance moved per time

Snail moves \(\frac{1}{2}\) foot per hour.
Question 5.
A fertilizer covers \(\frac{5}{8}\) square foot in \(\frac{1}{4}\) hour.
Answer:
Determine the units of the rate.
The rate is area covered in square feet per time in hours.
Find fertilizer’s rate of covering in area covered per time.

Fertilizer covers 2\(\frac{1}{2}\) square feet per hour.
Find each unit rate. Determine which is lower. (Example 2)
Question 6.
Brand A: 240 mg sodium for \(\frac{1}{3}\) pickle or Brand B: 325 mg sodium for \(\frac{1}{2}\) pickle
Answer:
First find rate in sodium per pickle at which each brand’s pickle contains sodium

To find the unit rates, first rewrite the fractions
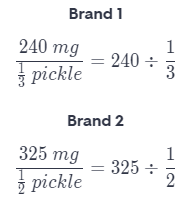
To divide, multiply with the reciprocal

Thus, Brand 2’s pickles contain less sodium.
Question 7.
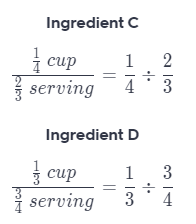
Ingredient C: \(\frac{1}{4}\) cup for \(\frac{2}{3}\) serving or Ingredient D: \(\frac{1}{3}\) cup for \(\frac{3}{4}\) serving
Answer:
First find rate in cup per serving at which each ingredient goes into the serving
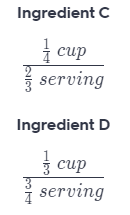
To find the unit rates, first rewrite the fractions.
To divide, multiply with the reciprocal.

Thus, Ingredient C has a lower cup per serving rate.
Essential Question Check-In
Question 8.
How can you find a unit rate when given a rate?
Answer:
When we are given a rate, we need to divide one measurement with the other to get unit rate.
Texas Go Math Grade 7 Lesson 2.1 Independent Practice Answer Key
Question 9.
The information for two pay-as-you-go cell phone companies is given.

a. What is the unit rate in dollars per hour for each company?
Answer:
First find rate in dollars per hour at which each company bills phone calls

To find the unit rates, first rewrite the fractions
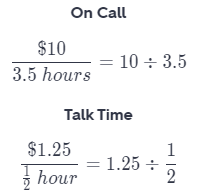
To divide, multiply with the reciprocal.
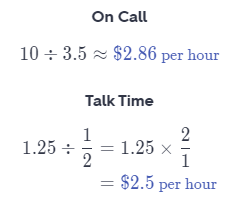
b. Analyze Relationships Which company offers the best deal? Explain your answer.
Answer:
Compare the unit rates.
On Cati \\\\Talk Time
2.84 \\\\\\\\> 2.5
Talk Time ¡s more affordable, because they charge Less for call.
c. What If? Another company offers a rate of $0.05 per minute. How would you find the unit rate per hour?
Answer:
We have to multiply the price by to 60 get dollars per hour.
0.05 × 60 = $3 per hour
d. Draw Conclusions Is the rate in part c a better deal than On Call or Talk Time? Explain.
Answer:
It is not, because they charge the most for a call, per hour.
Question 10.
Represent Real-World Problems Your teacher asks you to find a recipe that includes two ingredients with a rate of \(\frac{2 \text { units }}{3 \text { units }}\).
a. Give an example of two ingredients in a recipe that would meet this requirement.
Answer:
Corn flour and regular flour in unit of gram in a recipe for bread
b. If you needed to triple the recipe, would the rate change? Explain.
Answer:
The rate would not change. We would multiply both numerator and denominator by 3, that means the fraction would still have the same quotient.
Question 11.
A radio station requires DJs to play 2 commercials for every 10 songs they play. What is the unit rate of songs to commercials?
Answer:
First, divide number of songs by number of commercials.
10 ÷ 2 = 5
The unit rate of song to commercial is 5 songs for a commercial.
Question 12.
Multistep Terrance and Jesse are training for a long-distance race. Terrance trains at a rate of 6 miles every half hour, and Jesse trains at a rate of 2 miles every 15 minutes.
a. What is the unit rate in miles per hour for each runner?
Answer:
Find rate in miles per hour at which each runner trains.

To find the unit rates, first rewrite the fractions.
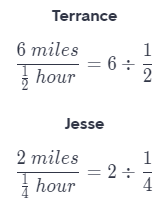
To divide, multiply with the reciprocal.

b. How long will each person take to run a total of 50 miles at the given rates?
Answer:
Divide each rate by 50.
Terrance:
\(\frac{50}{12}\) = \(\frac{25}{6}\)
= 4\(\frac{1}{6}\)
Jesse:
\(\frac{50}{8}\) = \(\frac{25}{4}\)
= 6\(\frac{1}{4}\)
Terrance would take 4\(\frac{1}{6}\) hours. Jesse would take 6\(\frac{1}{4}\) hours.
c. Sandra runs at a rate of 8 miles in 45 minutes. How does her unit rate compare to Terrance’s and to Jesse’s?
Answer:
Repeat as in a.
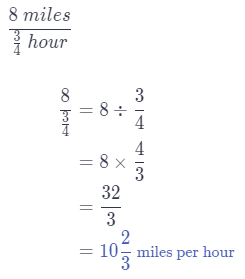
Sandra runs 10\(\frac{2}{3}\) miles per hour, that is faster than both Terrance and Jesse.
Question 13.
Analyze Relationships Eli takes a typing test and types all 300 words in hour. He takes the test a second time and types the words in hour. Was he faster or slower on the second attempt? Explain.
Answer:
He was faster the second time, because he read the same number of words in less time.
H.O.T.S Focus On Higher Order Thinking
Question 14.
Justify Reasoning An online retailer sells two packages of protein bars.
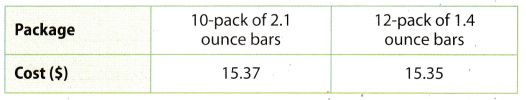
a. Which package has the better price per bar?
Answer:
Divide the cost by the number of bars:
10-pack:
15.37 ÷ 10 = 1.537
≈ 1.54
12-pack:
15.35 ÷ 12 ≈ 1.28
12-pack has a better price per bar.
b. Which package has the better price per ounce?
Answer:
10-pack has 10 × 2.1 = 21 ounces
12-pack has 12 × 1.4 = 16.8 ounces
Without calculating we can see that the 10-pack has a better price per ounce, because the difference in cost is negligible, but the 10-pack has significantly more ounces.
c. Which package do you think is a better buy? Justify your reasoning.
Answer:
10-pack is a better buy. It does not matter which pack has a better price per bar, but the better price per ounce.
Question 15.
Check for Reasonableness A painter painted about half a room in half a day. Coley estimated the painter would paint 7 rooms in 7 days. Is Coley’s estimate reasonable? Explain.
Answer:
Coley’s estimate is reasonable. If the painter paints half a room in half a day, that means he paints a room in a day. Thus, he paints 7 rooms in 7 days.
Question 16.
Communicate Mathematical Ideas If you know the rate of a water leak in gallons per hour, how can you find the number of hours it takes for 1 gallon to leak out? Justify your answer.
Answer:
Divide 1 hour by the rate of a water leak.
E.g.
The rate of a water leak is 4 gallons per hour.
That means it will take \(\frac{1}{4}\) hour for 1 gallon to leak out.